自适应群体结构的粒子群优化算法

孙文新，穆华平

(1.鹤壁职业技术学院电子信息工程学院，河南鹤壁458030;2.鹤壁职业技术学院 公共基础教研部，河南 鹤壁458030)

粒子群优化算法(particle swarm optimization，PSO)是一种启发式全局优化算法，由Kennedy和Eberhart[1]于1995年首次提出，其基本思想源于他们早期对鸟类群体行为的规律性研究.由于粒子群优化算法概念简单、参数少，且能根据当前的搜索情况动态调整搜索策略，已经在电力、化工、通讯和医学等[2-4]众多领域成功应用.然而在处理复杂环境中大规模的优化问题时，效果仍不能尽如人意.

研究证明[5]，粒子群算法中粒子间的关联形式能够直接影响到算法的优化性能.杨雪榕等[6]提出了一种多邻域的粒子群优化算法，粒子按照索引号划分成若干邻域，每个邻域的第1个粒子接受全局信息，其他粒子只接受邻域内的信息，这样就增加了邻域内粒子搜索的独立性;Matsushita等[7]基于WS、NW小世界网络模型和BA无标度模型，研究了静态群体结构与粒子群算法搜索性能之间的关系;穆华平等[8]提出一种基于小世界模型动态演化邻域的微粒群算法，群体结构从环形规则网络逐步进化为小世界网络，前期保证了种群的多样性，后期加快了收敛速度;彭虎等[9]提出一种动态邻域混合粒子群优化算法，将随机拓扑和冯诺依曼拓扑相结合形成动态邻域，使用粒子邻域全面学习搜索策略，提高算法的全局搜索能力.zhang等[10]根据微粒的度、适应值和微粒间的距离构建了一个动态的无标度结构演化过程.

从复杂网络的形成过程中受到启发，提出一种基于自适应群体结构的粒子群优化算法，粒子群体的结构模式以粒子的实际寻优过程和适应值为动力来引导形成.

1 粒子群优化算法概述

粒子群优化算法是一种基于迭代模式的优化方法，算法中引入“群体”和“进化”的概念，粒子根据适应值大小采用“速度－位置”模型进行搜索.群体中的每个粒子代表解空间中的一个解，解的优劣程度由适应函数决定.粒子群优化算法的数学描述如下[11]:

假设有N个没有体积和重量的粒子组成的群体在D维搜索空间中以一定的速度飞行，每个粒子在搜索时，考虑到了自己搜索到的历史最好位置和群体内(或邻域内)其他粒子的历史最好位置，在此基础上变化位置，寻找最优解.其中第i个粒子的当前位置Xi=[xi1xi2… xid];飞行速度Vi=[vi1vi2… vid];粒子 i 所经历的最好位置Pi=[pi1pi2… pid]，个体的最好位置Pig=[pig1pig2… pigd]代表邻域i内所有粒子经历过的最好位置.粒子在找到个体最优位置和全局最优位置后，根据式(1)和(2)更新自己的速度和位置:

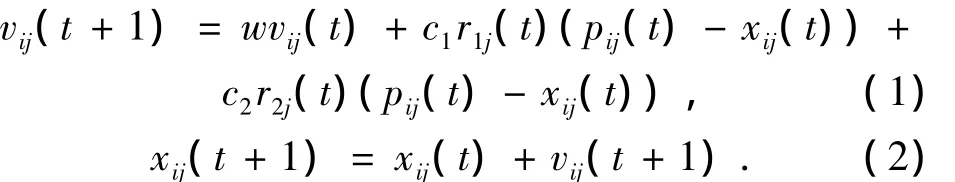
式中:w称为惯性权重，用来调整粒子的全局和局部搜索能力;c1、c2为学习系数，使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优位置以及群体内或领域内的全局最优靠拢;r1、r2是(0，1)的随机数，使算法具有一定的随机性.上述模型为粒子群优化算法的局部最优模型(Lbest模型)，若式(1)中第3部分的趋向位置是全局最优位置时为全局最优模型(Gbest模型).

2 自适应群体结构的粒子群优化算法

2.1 自适应群体结构思想

尽管粒子群优化算法在许多优化问题上都取得了很好的优化性能，但依然存在后期搜索速度慢和“早熟收敛”的问题.这是因为算法在搜索后期，众多粒子都拥挤在历史最好位置周围，无法逃离局部最优而不断进行重复性的无效搜索.为了提高算法的空间搜索能力，同时又保留局部快速收敛的优良性能，本文根据粒子群体在不同阶段搜索模式的要求，采用自适应群体结构来调整算法的搜索能力.

观察现实中的许多网络，发现大多数网络的形成过程往往是从最初的孤立节点开始，由于某种称为“择优连接”的动力学原因而关联在一起，最终形成了复杂网络.结合粒子群优化算法的搜索特性，考虑将复杂网络形成过程中凸显的这种现象移植到粒子群优化算法中.为避免早熟收敛，将多样性函数做简单改进[8]，用邻域内最优位置代替群体平均位置，具体定义如式(3):

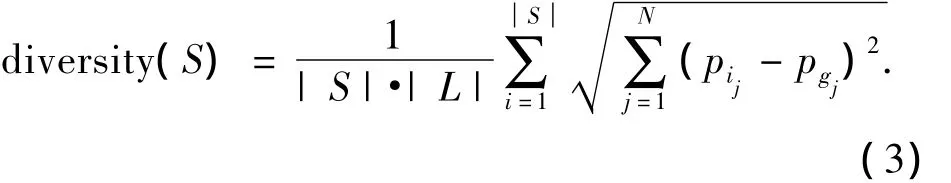
式中:|S|为邻域内粒子的个数，|L|为搜索空间的最长对角线的长度，N为问题的维数，pij为第i个粒子的第j维分量，pgj为邻域内的最优位置的第j维分量.

算法首先将粒子群体初始化为具有少量连接的随机网络，每个粒子都带有一个搜索标志flag，并且初始化状态 flag=1.若当前搜索优于前一次搜索，表明本次搜索成功，则flag=l，否则设置flag=0，此时检测该粒子邻域的群体多样性，如果粒子过于集中在pgj附近，导致多样性过低，即diversity(Si)＜dLow时，在种群中随机选择该邻域以外的其他粒子建立连接，否则原有连接保持不动.

这样，在算法初期，群体结构松散，有利于保持群体的多样性，可以获取尽可能多的候选解;随着新连接的不断加入，由于受到最优位置的引导，群体中部分粒子以接近Gbest模型的寻优方式进行搜索，多数粒子以接近Lbest模型的寻优方式进行搜索，在全局搜索和局部搜索之间获得了很好的折衷;到了算法后期，算法基本围绕在全局最优附近搜索，此时群体连接更加密集，形成高连通度的群体结构，有利于粒子对最优解所在的空间内进行深度的细致搜索，进而保证算法以较快的速度搜索到全局最优位置.

2.2 惯性权重的调整

在粒子群优化算法中，搜索陷入局部极值，往往表现为算法重复进行无效的搜索，而粒子的位置几乎静止不变.为了充分发挥自适应群体结构的效能，本文根据适应函数值的不同采用不同的惯性权重，以求全局最小值为例，群体中的粒子按适应值fi的变化情况分为以下3种情况:

1)群体中满足fi＜f'arg的粒子已经比较接近全局最优，此时应赋予较小的惯性权重，以促进快速收敛于全局最优.因此将此集合中的粒子的惯性权重调整为

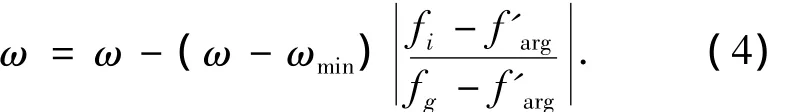
取ωmin=0.5，由式(4)可以看出，粒子的适应值越好，其对应的惯性权重就越小，进而加强了局部寻优的能力.

2)如果粒子满足f'arg＜fi＜farg，则说明这些粒子具有较好的局部和全局的寻优能力，此时应保证在前期粒子进行“开发”性搜索，获得较多候选解，后期进行“勘探”性搜索，探索出全局最优.因此考虑这部分粒子采用经典的惯性权重线性递减的调整方法.

3)对于群体中较差的粒子，即fi＞farg时，借鉴吴浩扬等[12]提出的变异方法来调整惯性权重:

当群体搜索到的最优位置长时间未发生变化时，群体根据粒子的分布特点来调整惯性权重.若粒子分布较为分散，则Δ取较大的值来降低粒子的惯性权重，加强局部寻优，使群体趋于收敛;若粒子分布较为聚集，算法陷入局部最优，则Δ取较小的值增加粒子的惯性权重，促使粒子有效地跳出局部最优.其中参数k主要用来调整惯性权重的上限，文中取 k=1.5.

2.3 算法流程

根据以上分析，基于 SPS-PSO(particle swarm optimization based on self-adaptive population structure，SPS-PSO)的基本步骤为:先初始化种群;设置初始化的状态标志flag=1;计算每个粒子的适应值，并且评估个体的历史最好位置和全局最好位置;果当前位置优于前一次搜索，则flag=l，否则设置flag=0;若连续t次flag的值始终为0，此时检测该粒子邻域的群体多样性，与最优粒子建立新的连接，并依据适应值重新计算ω的值，然后更新粒子的速度和位置，进行下一步的搜索.

SPS-PSO算法的流程图如图1.

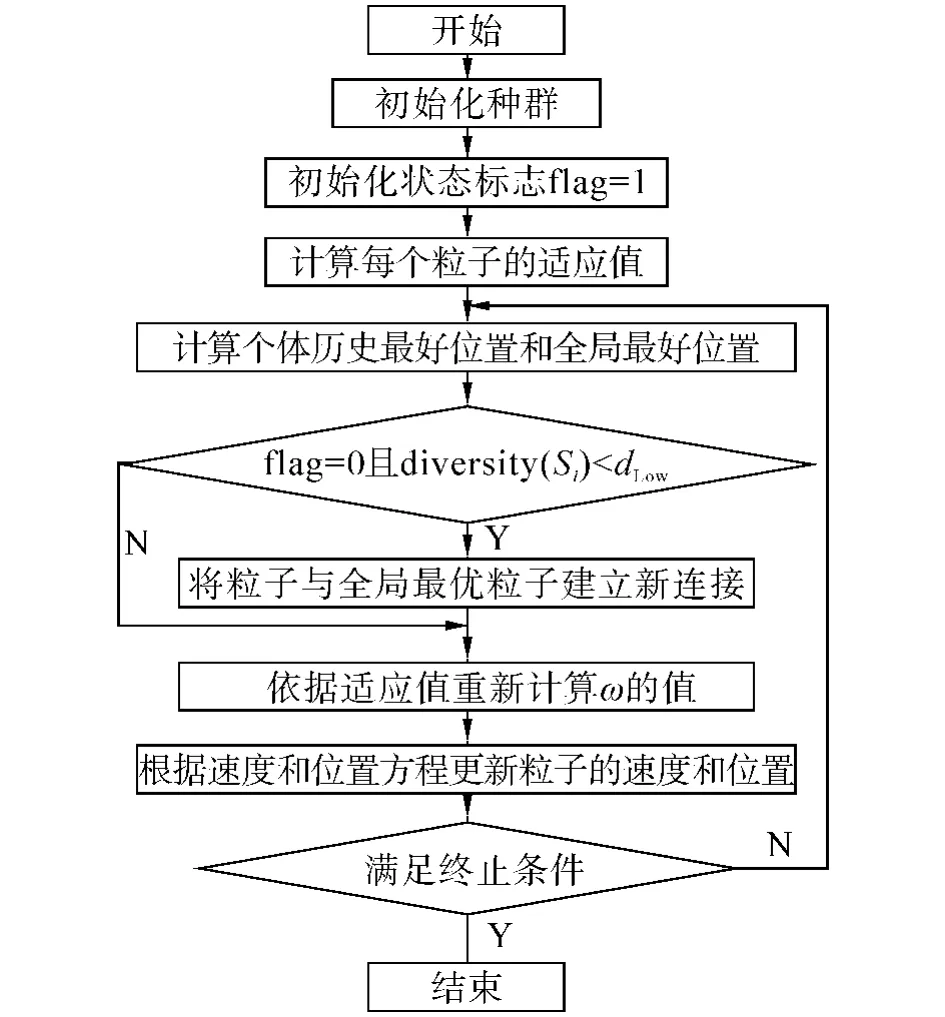
图1 SPS-PSO算法流程Fig.1 Flow chart of SPS-PSO algorithm

3 仿真实验

3.1 测试函数和参数设置

为了测试新算法对复杂问题寻优的有效性，本文选取了3个Benchmark测试函数进行仿真实验.实验环境为Intel CPU 2.1 GB，Windows XP操作系统、1.0 GB 内存，Visual C++6.0 环境下进行编程.为确保实验结果的可信度，每个算法运行20次实验，初始化种群个数为100，问题维数30维，最大进化代数为1 000.算法中，加速因子 c1、c2均取 1.5，ω的初始值取 0.9，dLow取5 ×10－6.

1)Sphere函数.

Sphere函数为可分离的单峰函数，用于测试算法的收敛精度，函数在xi=0处到达全局极小值0.

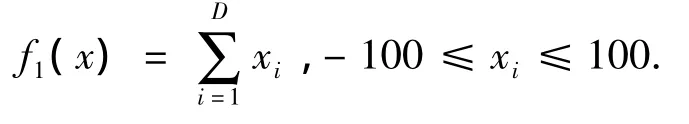
2)Rastrigrin函数.

Rastrigrin函数是不可分离的多峰函数，较难优化，全局最小值在变量为0时到达，该函数有10n个局部极小点.

3)Griwank函数.

Griwank函数也是不可分离的多峰优化函数，函数在xi=0时到达全局最小值，该函数有2n个局部极小值.

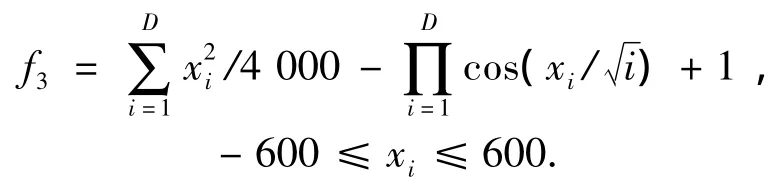
3.2 实验结果与分析

为了测试新算法的优化性能，本文将标准PSO算法、DSWN-PSO(particle swarm optimization with dynamic evolutionary neighbourhood of small-world model)[8]和 DNH-PSO(dynamic neighborhood hybrid-PSO)[9]进行对比分析.图2显示了Sphere函数的优化对比结果.通过比较可以看出，SPS-PSO算法始终保持较快的收敛速度，并且最终获得了比DSWNPSO算法和DNH-PSO算法更好的优化性能.

图2 30维Sphere函数优化对比Fig.2 Comparison of optimizing on 30-D Sphere

从图3中可以看出，对于Rastrgin函数来说，SPS-PSO算法能在较短的时间内获得明显的优化效果，并且仍然呈向全局最优的趋势.算法在400～600代时，有一个相对平坦的优化过程，这说明算法在此期间停留在局部最优位置上徘徊不前，但最终因为网络形成过程中根据适应值择优连接的过程，使得算法能及时从局部最优位置跳出来，突破了局部最优的束缚，继续向全局最优位置靠近.

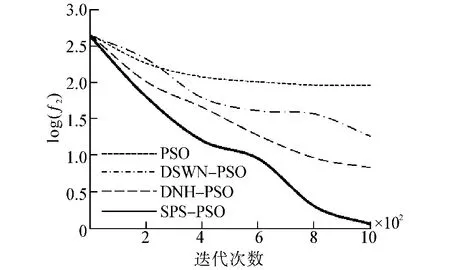
图3 30维Rastrgin函数优化对比Fig.3 Comparison of optimizing on 30-D Rastrgin

Griewank函数是一个多峰、存在许多局部极小值且自变量之间互相影响的、典型的非线性多模态函数，极易陷入局部最优，从图4中可以看出，SPSPSO算法能以较快的速度收敛于全局最优，并且在实验中发现其收敛成功率为100%.其原因在于新连接的加入能适应算法的收敛状态，使得算法具有较强的抗早熟能力，能够突破中期短暂的停滞阶段，获得正确的搜索方向.

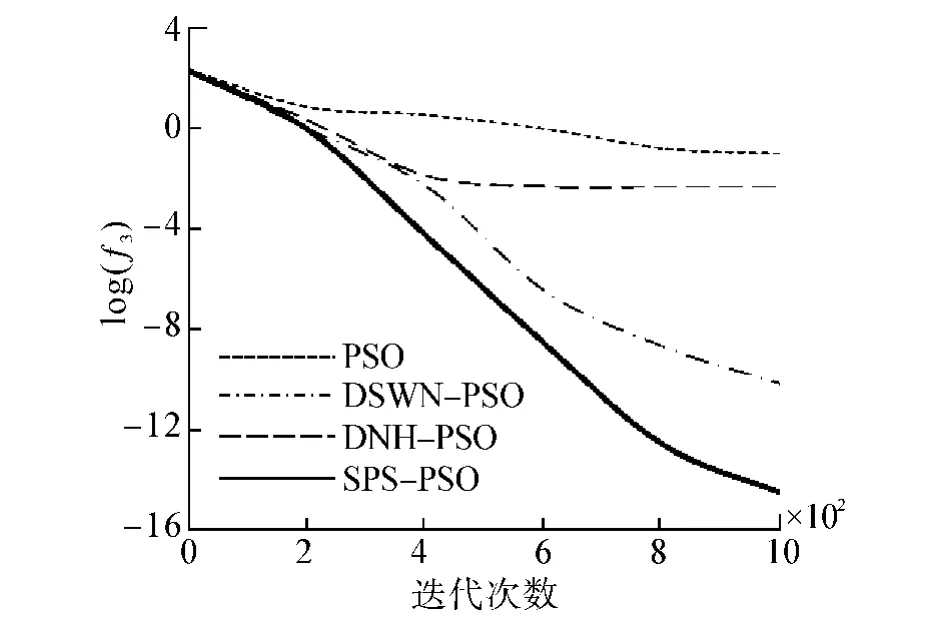
图4 30维Griewank函数优化对比Fig.4 Comparison of optimizing on 30-D Griewank

从实验中发现，SPS-PSO算法的执行效率要高于DSWN-PSO算法，这是因为SPS-PSO算法中，搜索前期的粒子在空间中分布较为均匀，因此通过flag参数作为阈值参数来检测粒子的搜索状态，避免了前期不必要的多样性检测，提高了算法的效率，中后期多样性函数的检测一定程度上避免了算法的局部收敛，促使算法进一步向全局最优靠近.

4 结束语

本文将复杂网络形成过程中的动力学机制引入粒子群优化算法中，并根据搜索状态调整惯性权重以适应搜索要求，提出了一种自适应群体结构的粒子群优化算法.随着算法的搜索，利用多样性函数检测邻域多样性，使群体结构从低连通度的分散结构进化为连通度较高的复杂网络，由于其进化过程符合粒子群优化算法对信息共享模式的要求，因此极大地提高了算法的性能.下一步工作将通过对最终形成的群体结构的特性做详细研究，以探索更符合粒子间信息交流的群体结构.

[1]KENNEDY J，EBERHART R.Particle swarm optimization[C]//Proc IEEE International Conference on Neural Networks.Perth，Australia，1995:1942-1948.

[2]POLI R.An analysis of publications on particle swarm optimization applications[R].London:Department of Computer Science，University of Essex，2007.

[3]POLI R，KENNEDY J，BLACKWELL T.Particle swarm optimization:an overview[J].Swarm Intelligence，2007，1(1):33-57.

[4]KENNEDY J，MENDES R.Population structure and particle swarm performance[C]//Proceedings of the IEEE Congress on Computation Intelligence.Honolulu，USA，2002:1671-1675.

[5]钱晓山.一种改进的混沌粒子群优化混合算法[J].应用科技，2012，39(1):5-8.QIAN Xiaoshan.A hybrid algorithm of the improved chaotic particle swarm optimization[J].Applied Science and Technology，2012，39(1):5-8.

[6]杨雪榕，梁加红，陈凌，等.多邻域改进粒子群算法[J].系统工程与电子技术，2010，32(11):2453-2458.YANG Xuerong， LIANG Jiahong，CHEN Ling， et al.Multi-neighborhood improved particle swarm optimization algorithm[J].Systems Engineering and Electronics，2010，32(11):2453-2458.

[7]MATSUSHITA H，NISHIO Y.Network-structured particle swarm optimizer with various topology and its behaviors[J].Lecture Notes in Computer Science，2009，5629:163-171.

[8]穆华平，曾建潮.基于小世界模型动态演化邻域的微粒群算法[J].系统仿真学报，2008，20(15):3940-3943.MU Huaping，ZENG Jianchao.Particle swarm optimization with dynamic evolutionary neighbourhood of small-world model[J].Journal of System Simulation，2008，20(15):3940-3943.

[9]彭虎，张海，邓长寿.动态邻域混合粒子群优化算法[J].计算机工程，2011，37(14):211-213.PENG Hu， ZHANG Hai， DENG Changshou.Dynamic neighborhood hybrid particle swarm optimization algorithm[J].Computer Engineering，2011，37(14):211-213.

[10]ZHANG Chengong，YI Zhang.Scale-free fully informed particle swarm optimization algorithm[J].Information Sciences，2011，181(20):4550-4568.

[11]曾建潮，介婧，崔志华.微粒群算法[M].北京:科学出版社，2004:5-10.

[12]吴浩扬，朱长纯，常炳国，等.基于种群过早收敛程度定量分析的改进自适应遗传算法[J].西安交通大学学报，1999，33(11):27-30.WU Haoyang，ZHU Changchun，CHANG Bingguo，et al.Adaptive genetic algorithm to improve group premature convergence[J].Journal of Xi’an Jiaotong University，1999，33(11):27-30.