视线测量光学导航系统观测模型选取

李建国 崔祜涛 田阳

（1哈尔滨工业大学深空探测基础研究中心，哈尔滨150080）（2中国人民解放军61345部队，西安710010）

1 引言

随着光学敏感器的发展，视线测量自主光学导航技术在太空任务特别是深空探测领域中得到了广泛的关注[1-3]。导航系统对光学设备的依赖使得选取高精度的测量敏感器成为必要。但当存在较高的测量精度时，测量模型非线性与测量噪声对导航性能的影响是同等重要的，特别在初始状态估计误差较大的情况下，忽略测量模型非线性高阶项会使滤波算法发散或收敛到错误的状态估计值[4]。因此，对于高精度测量设备，测量模型非线性对导航精度的作用至关重要。

基于局部线性化的扩展卡尔曼滤波（Extended Kalman Filter，EKF）已被成功用于众多导航系统来处理非线性滤波问题[3]。作为一种近似非线性滤波器，EKF假设系统的非线性模型可以由当前状态展开的线性模型很好的近似。因此为了使EKF获得最优的滤波性能，应该尽可能选择非线性强度弱的测量模型，并对非线性高阶项进行补偿。尽管导航系统可以考虑更先进的非线性滤波算法，但任务的实时性使得粒子滤波（Particle Filtering，PF）不适合工程要求[5]，无迹卡尔曼滤波（Unscented Kalman Filter，UKF）需要在线调节滤波参数，不一定能在实际应用中取得满意的效果[6]。所以在导航系统设计时，定量测量非线性估计问题中模型的非线性强度，可以为导航系统设计时测量模型和滤波算法的选择提供参考。

光学敏感器测量模型主要分为焦平面测量模型和单位矢量测量模型[7]。焦平面测量模型直接与实际的物理观测量和测量噪声相关联，是光学敏感器基本的测量模型。单位矢量测量模型由共线方程非线性转换得到，并对测量噪声统计特性进行了简化[8]，广泛应用于姿态确定算法中。文献[9]认为单位矢量测量模型比焦平面测量模型非线性强度低，可以产生更好的估计性能。但其结论建立在单个例子的仿真分析上，缺乏理论分析和通用性。

本文基于微分几何非线性强度测量理论10，从理论上分析了不同测量模型的非线性强度，并以基于视线矢量观测的高精度定姿任务为例，比较了两种测量模型对滤波精度的影响，最后通过仿真验证了理论分析结果。

2 视线测量光学导航算法

2.1 观测方程

假设视线矢量测量由导航相机给出，对其测量模型作如下简化处理：相机坐标系的Z轴沿着视轴方向；飞行器体坐标系与相机坐标系重合；导航相机视为理想的小孔成像相机；测量噪声建模为独立的零均值高斯白噪声。

导航相机通过测量天体视线方向偏离视轴的方位角来确定飞行器位姿，图1给出了测量原理图[10]。飞行器位置、姿态与观测量之间的关系可由式（1）给出。

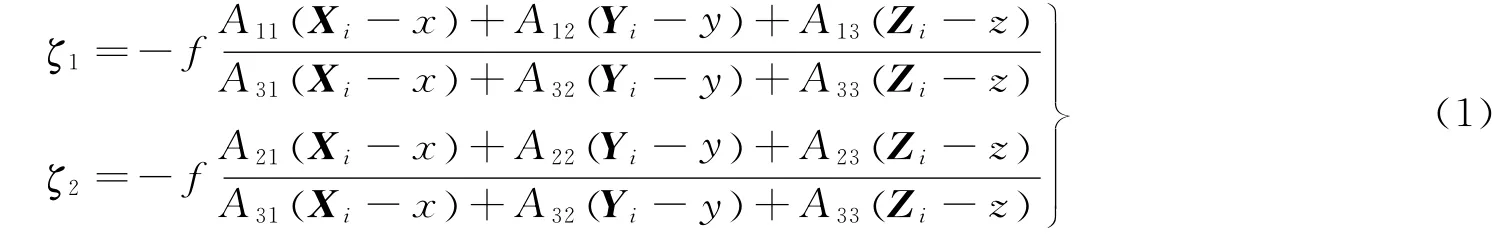
式中 （ζ1，ζ2）是天体视线方向在焦平面上的投影值；（Xi，Yi，Zi）是已知的天体位置；（x，y，z）是未知的飞行器的位置；Aij（i，j＝1，2，3）为姿态矩阵A的各分量；f为已知的导航相机焦长，一般假设其值为1。如果目标天体位于无穷远处，式（1）简化为星敏感器共线测量方程。

在考虑测量噪声的情况下，k时刻的焦平面测量模型可表示为

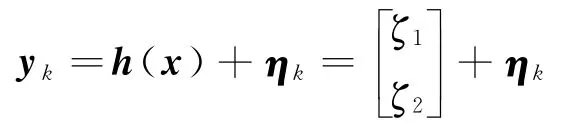
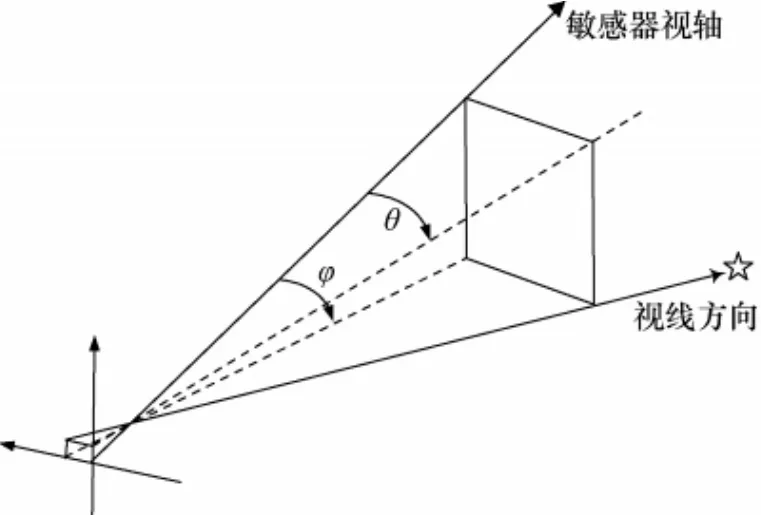
图1 相机测量几何Fig.1 Measurement geometric sketch of camera

式中yk为目标天体在焦平面上的测量值；h（x）为测量函数，x为飞行器的状态矢量；ηk为零均值高斯白噪声，在实际工程应用中广泛使用的测量噪声方差矩阵为[7]

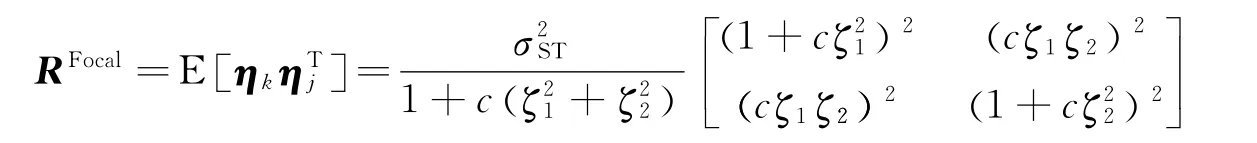
式中c为量纲为1的常数；σ2ST为相机主点的测量噪声方差强度。

经过非线性转换，共线测量方程可以表示为单位矢量形式：

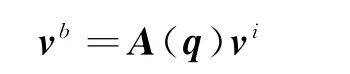
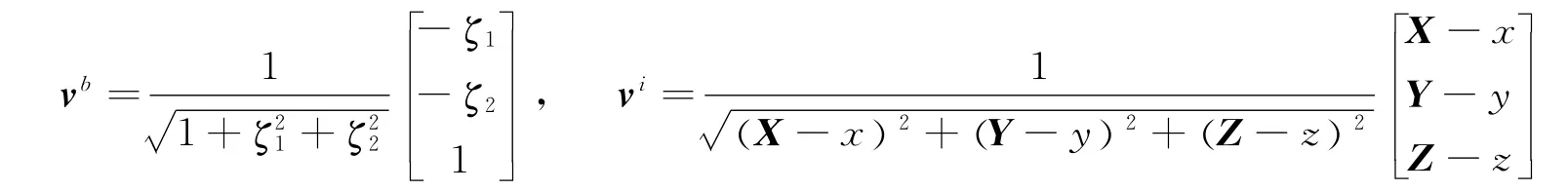
当焦平面测量模型转化为单位矢量测量模型时，相应的测量噪声也要进行转化，表现为与测量值耦合在一起的乘性噪声。Shuster在EKF算法框架内，提出了一个简化的测量噪声方差模型[8]：

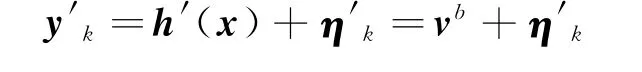
其中测量噪声方差特性满足

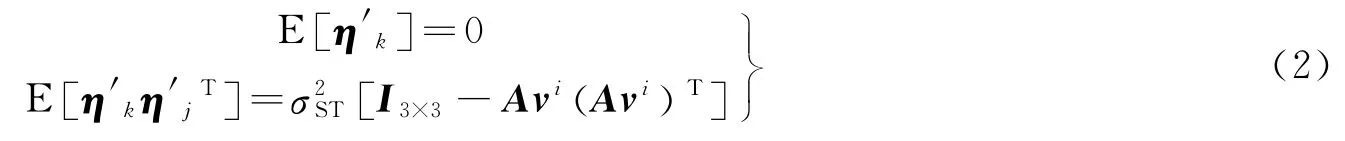
由于单位矢量的归一化约束使得测量方差矩阵奇异，在实际工程应用中可使用一个无奇异的测量噪声方差矩阵代替：

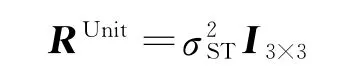
2.2 测量模型非线性

为了分析测量模型非线性对滤波性能的影响，本节比较了标准EKF和二阶EKF的测量更新过程。不失一般性，将非线性测量模型表示为如下形式

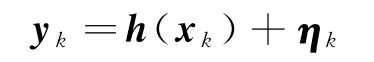
测量误差方程和测量残差方差矩阵可以分别写为

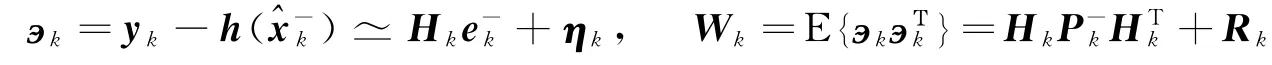
其中，测量敏感性矩阵定义为

基于上述定义，可以得到先验和后验状态估计误差方差之间的关系式：

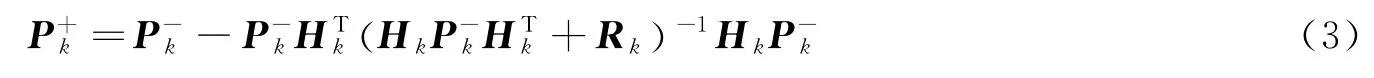
当测量模型非线性强度较大时，考虑其泰勒级数二阶展开项：

其中，Hessian矩阵定义为

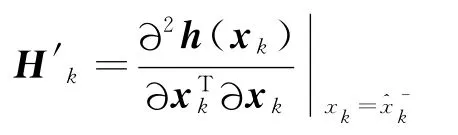
考虑二阶项影响的测量函数预测估计值，变为

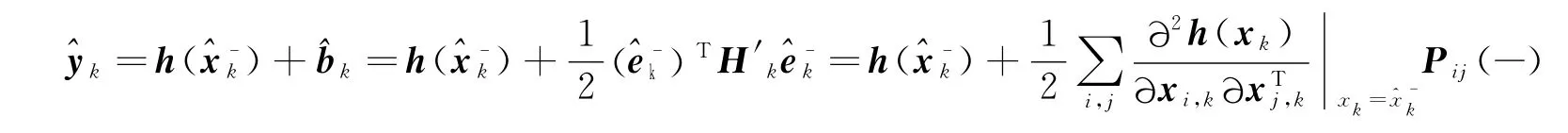
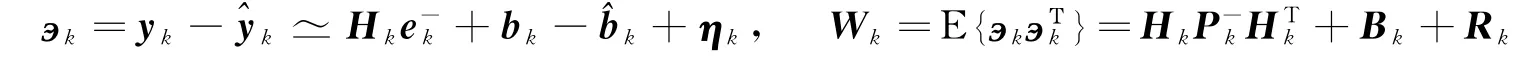
后验误差方差矩阵的表达式变为

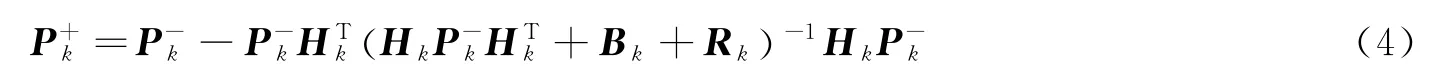
将式（3）与式（4）进行比较可知，当存在精确观测值时，测量误差变得很小，使得Bk与Rk的大小处于同一数量级，若将测量模型泰勒级数高阶展开项忽略，则EKF计算得到的估计误差方差要比实际的估计误差小，使得滤波器误认为已经达到了要求的精度。从而使测量更新值不能最优融合，导致滤波发散或者收敛到错误的稳态值。因此，在基于EKF的导航算法中，对于高精度光学敏感器，选择非线性强度低的观测方程可以有效降低模型非线性对算法的影响。

3 基于微分几何曲率测量的非线性强度分析

导航系统非线性依赖于观测几何、运动学及动力学模型的数学描述形式，但一直缺乏定量的测量方法。下面首先给出非线性曲率测量的定义，然后将其应用于姿态估计问题中。

3.1 非线性曲率测量

将非线性测量模型在先验估计值处进行泰勒级数展开：

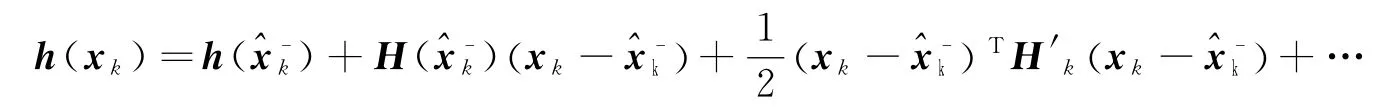
从几何概念理解，EKF中的线性化近似等价于使用处的切平面近似非线性曲面。要使滤波算法使用的线性近似有效，测量函数在邻域内必须相对平坦，即二阶项大小与一阶项大小相比是可以忽略的。基于这种思想，Bates和Watts提出了非线性强度的定量测量方法[11]。

右岸接头土坝在麻石水电站扩建工程已建而扩建船闸未建时填筑，上游坡比为1∶2.0，下游坡比1∶1.5；采用黏土心墙防渗的型式，基础布置帷幕灌浆。

首先将几何学中的垂直投影概念推广至n维欧式空间，可得到将Hessian矩阵H′k投影到切空间的正交投影矩阵[12]

式中Hk构成了切空间的正交基。则Hessian矩阵投影到切空间和正交空间的分量分别为

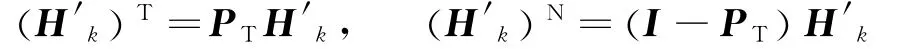
将二阶项分解到切空间和正交空间的分量分别与一阶项相比较，就可以得到参数效应曲率和固有曲率：

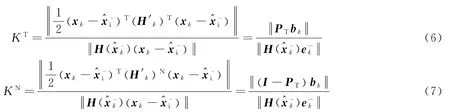
KT不但与数学模型相关，而且与测量模型采用的参数描述形式有关，KN则反映了非线性测量函数曲面的本质特性，与系统所采用的描述模型无关。参数效应曲率越小，对应的非线性模型的特性越接近线性模型，滤波性能越好。对于基于四元数的飞行器姿态估计问题，系统非线性主要由测量模型引入，测量模型非线性在确定状态估计最优值时起着重要作用。

3.2 测量模型非线性强度分析

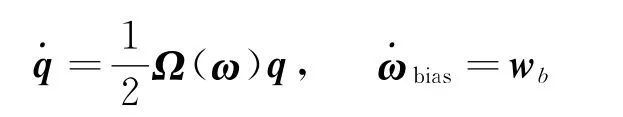
式中ω为角速度矢量，一般通过陀螺来测量；wb为高斯白噪声。

由式（6）和式（7）中的定义可知，为了比较不同测量模型的非线性曲率，首先需要计算测量敏感性矩阵。对观测方程直接求解Jacobi矩阵和Hessian矩阵涉及较大的计算量，本文采用修正罗德里格参数描述局部乘性姿态误差，避免了对姿态矩阵求偏导数。由四元数乘积定义可得

式中为单位四元数姿态估计值；a为三维姿态参数，描述与q之间的姿态误差δqa（）。为了使a与实际的误差旋转角φ一致，将其定义为四倍的修正罗德里格参数[14]

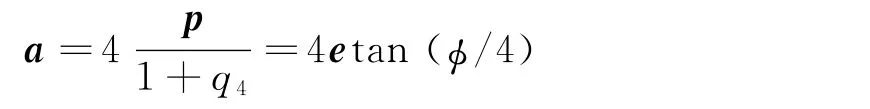
由于测量模型不依赖于陀螺偏差矢量，则一阶测量敏感性矩阵为

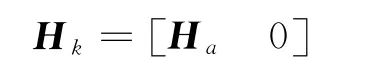
将式（8）和式（9）代入式（4）并取其一阶近似可得

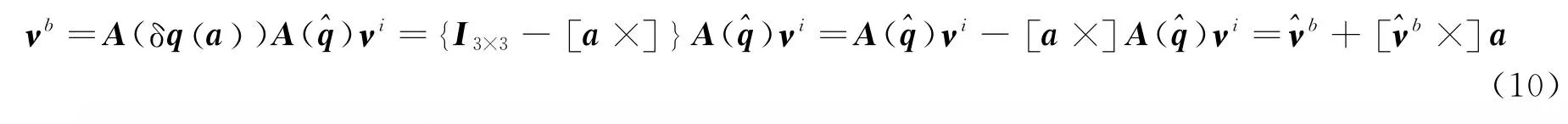
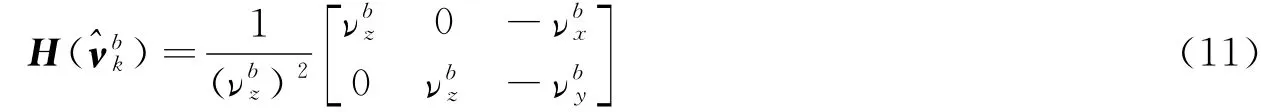
综合式（10）、（11）可得其一阶测量敏感性矩阵为

对于单位矢量测量模型，由于h′（x）＝νb，所以对应的一阶测量敏感性矩阵为

为了求解Hessian矩阵，首先考虑二阶项对测量函数的影响，同时将约束条件扩展到二阶，则测量方程可表示为

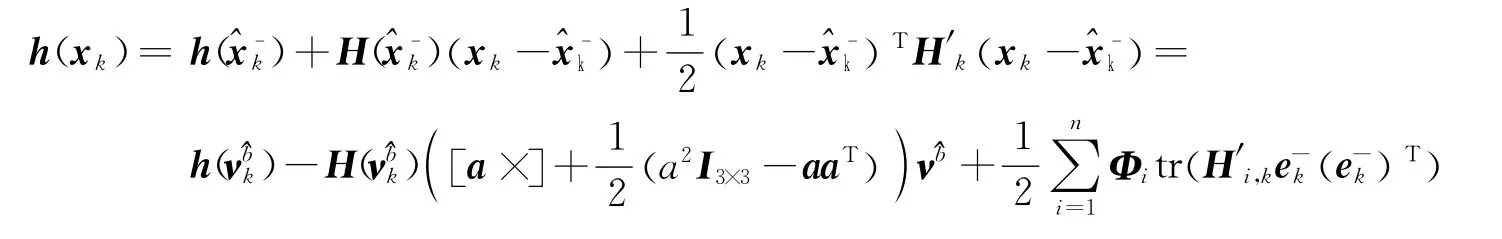
式中

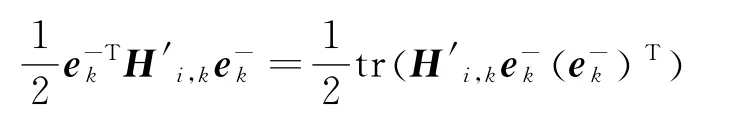
式中H′i，k表示Hessian矩阵H′k的第i面；Φi代表n个基矢，n是测量函数列矢量的个数。根据姿态误差定义可知

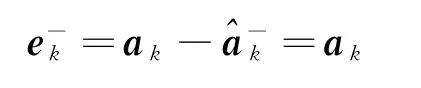
则测量方程二阶项表达式为

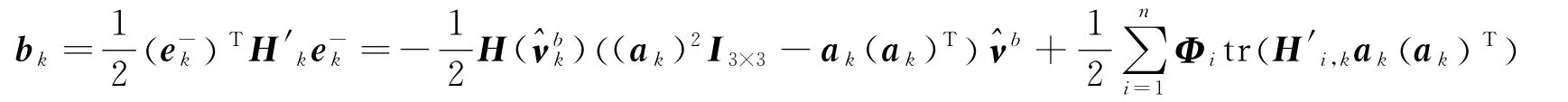
由于ak为姿态真实值，无法精确得到，因此使用估计值近似代替，这样就变为如下形式

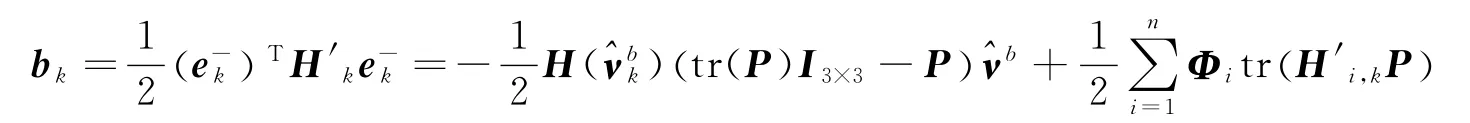
为了减少计算量，便于比较，对方差矩阵P做如下假设

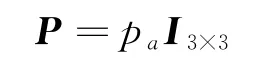
则测量函数二次项为

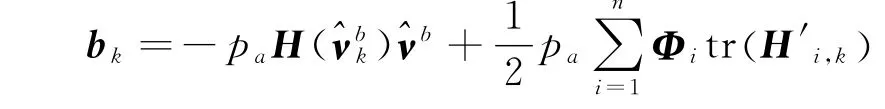
对于焦平面测量模型，由于

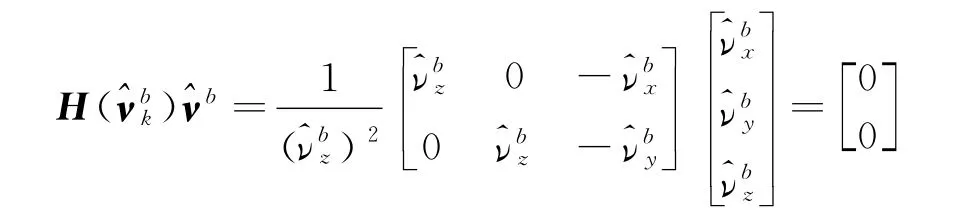
所以

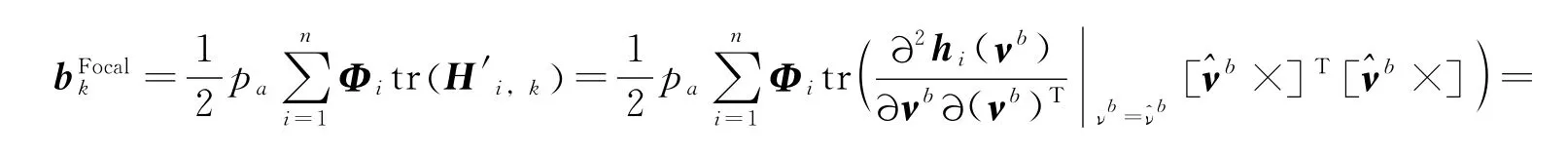
对于单位矢量测量模型，由于

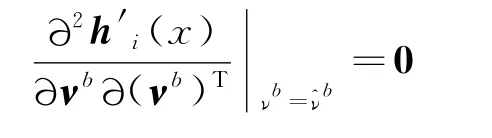
所以

从上述理论分析过程可知，式（12）和式（13）分别给出了两种测量模型对应的一阶测量敏感性矩阵，根据式（5）可以进一步获得投影到切空间的正交投影矩阵，泰勒级数二阶展开项则分别由式（14）和式（15）给出，这样测量模型非线性曲率就可以根据式（6）和式（7）计算得到。

4 仿真分析

为了验证上述所提到的非线性强度测量理论，以基于视线矢量测量的飞行器姿态确定为背景进行数学仿真分析，比较不同测量模型对姿态估计精度和收敛性能的影响。

由于采用两个非共线的测量矢量就能够唯一确定飞行器的姿态，所以为了简化测量敏感性矩阵的计算，惯性参考单位方向矢量取为 [1 0 0]T和 [0 1 0]T。星敏感器视场角为5°×5°，测量周期为2s，测量精度为10″。陀螺测量白噪声强度为0.02（°）／h1／2，漂移白噪声强度为0.1（°）／h3／2，采样周期为0.1s。采用四阶龙格-库塔法对传播方程进行离散化。由于星敏感器和陀螺采样周期的不同，假定每20个陀螺采样周期状态估计值更新一次。

为了使两种模型的非线性曲率测量之间的对比更加明显，初始姿态估计误差选取为100°，初始陀螺漂移估计误差选取为150（°）／h。角速度假设为 [0.1 0.03 0.03]Trad／s。图2和图3分别给出了观测模型的参数效应曲率和固有曲率测量值。它们都能够定量测量模型的非线性强度，但参数效应曲率与测量模型的具体描述形式有关，而固有曲率反映了测量模型的固有特性，因此图2中两个模型的曲率测量值差别很大，而图3中的差别则很小。从仿真结果可看出，单位矢量测量模型具有更低的非线性强度。由于四元数姿态估计问题中非线性主要由测量模型引入，测量模型非线性强度大小直接影响滤波算法性能。因此，为了进一步验证曲率测量理论的有效性，在上述仿真条件下，比较不同测量模型的姿态估计精度和收敛特性，图4和图5为100次蒙特卡罗仿真的姿态估计误差平均值。由仿真结果可知，在初始状态估计误差较大情况下，使用非线性强度较高的焦平面测量模型的光学导航算法不能够快速收敛至正确的稳态值，而基于单位矢量测量模型的光学导航算法则具有更高的估计精度和更快的收敛特性，即滤波算法性能与非线性曲率的变化一致，进一步验证了非线性曲率测量能够真实反映模型的非线性强度。因此，单位矢量测量模型更适合于光学导航系统，这种优势在初始估计误差较大和使用高精度测量设备时更为突出。

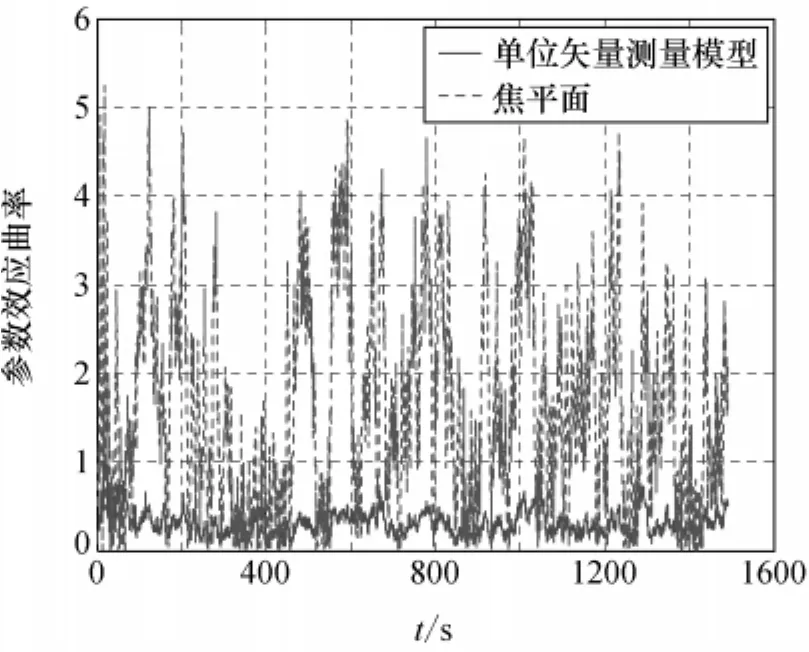
图2 测量模型的参数效应曲率比较值Fig.2 Comparison of parameter-effect curvature between measurement models

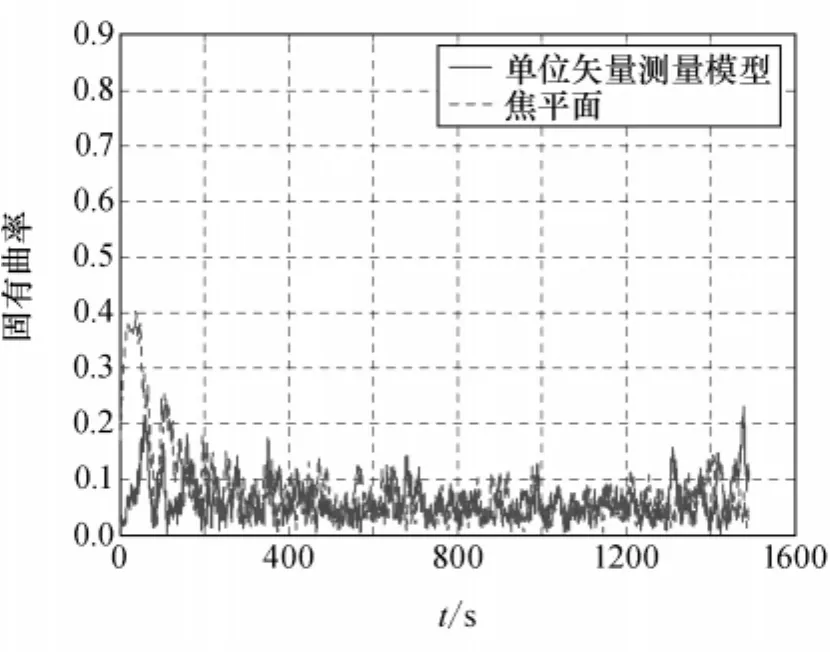
图3 测量模型的固有曲率比较值Fig.3 Comparison of intrinsic curvature between measurement models

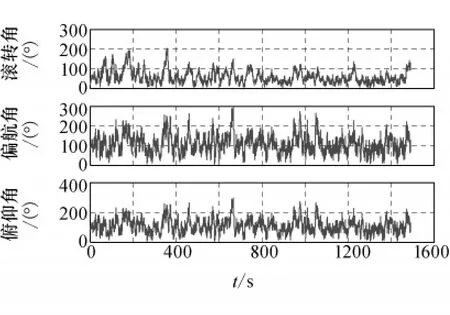
图4 焦平面测量模型姿态估计误差Fig.4 Attitude estimation errors of focal plane measurement model

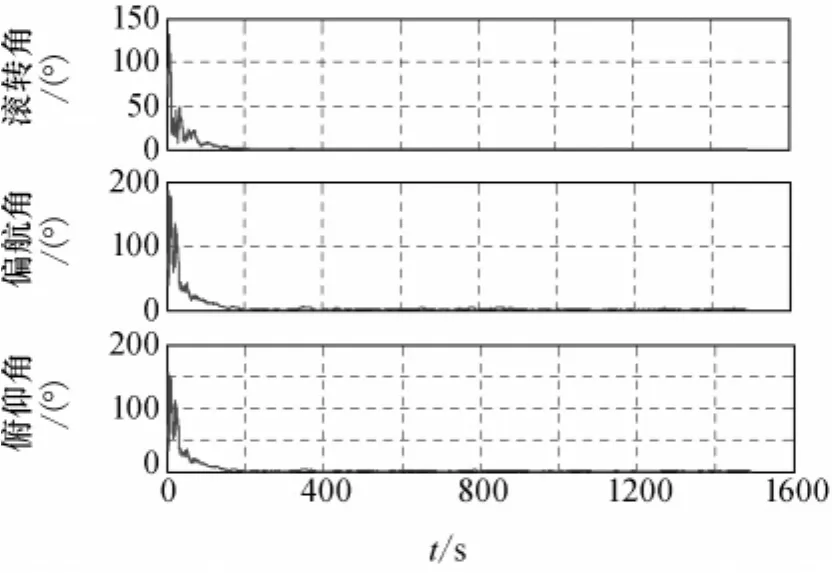
图5 单位矢量测量模型姿态估计误差Fig.5 Attitude estimation errors of unit vector measurement model

5 结束语

针对高精度光学导航系统测量模型选取问题，分析了测量模型非线性对导航性能的影响，并将微分几何曲率测量理论应用于姿态估计问题中，研究了焦平面测量模型和单位矢量测量模型的非线性强度。仿真结果表明，单位矢量测量模型在估计精度和收敛特性等方面的性能更为优越，非线性曲率与导航系统性能保持一致，适合作为飞行任务前的数学仿真分析工具。

今后的工作将针对非线性滤波问题中滤波不一致的现象，研究合适的非线性补偿方法，使得测量更新阶段信息融合达到最优。

[1]BAYARD D S，BRUGAROLAS P B.On-board vision-based spacecraft estimation algorithm for small body exploration [J].IEEE Transactions on Aerospace and Electronic Systems，2008，44（1）：243-260.

[2]LI S，CUI P Y，CUI H T.Vision-aided inertial navigation for pinpoint planetary landing [J].Aerospace Science and Technology，2007，11（6）：449-506.

[3]TRAWNY N，MOURIKIS A I，ROUMELIOTIS S I，et al.Vision-aided inertial navigation for pin-point landing using observations of mapped landmarks[J].Journal of Field Robotics，2007，24（5）：357-378.

[4]PEREA L，HOW J，BREGER L，et al.Nonlinearity in sensor fusion：divergence issues in EKF，modified truncated SOF，and UKF [C].AIAA Guidance，Navigation and Control Conference and Exhibit，Hilton Head，USA，August 20-23，2007.

[5]CRASSIDIS J L，MARKLEY F L，CHENG Y.Survey of nonlinear attitude estimation methods [J].Journal of Guidance，Control and Dynamics，2007，30（1）：12-28.

[6]ZANETTI R，DEMARS K J，BISHOP R H.Underweighting nonlinear measurements [J].Journal of Guidance，Control and Dynamics，2010，33（5）：1670-1675.

[7]SHUSTER M D.Kalman filtering of spacecraft attitude and the QUEST model[J].The Journal of the Astronautical Sciences，1990，38（3）：377-393.

[8]SHUSTER M D，OH S D.Three-axis attitude determination from vector observations [J].Journal of Guidance，Control and Dynamics，1981，4（1）：70-77.

[9]CHENG Y，CRASSIDIS J L.Particle filtering for sequential spacecraft attitude estimation [C].AIAA Guidance，Navigation and Control Conference and Exhibit，Providence，USA，August 16-19，2004.

[10]VATHSAL S.Spacecraft attitude determination using a second-order nonlinear filter [J].Journal of Guidance，Control and Dynamics，1987，10（6）：559-566.

[11]BATES D M，WATTS D G.Nonlinear regression analysis and its application [M].New York：John Wiley，1988.

[12]程云鹏，张凯院，徐仲.矩阵论 [M].西安：西北工业大学出版社，2001：289-293.

[13]章仁为.卫星轨道姿态动力学与控制 [M].北京：北京航空航天大学出版社，1998：139-149.

[14]MARKLEY F L.Attitude error representations for Kalman filtering [J].Journal of Guidance，Control and Dynamics，2003，26（2）：311-317.