一种高精度GPS卫星钟差预报方法

陶庭叶 高飞 李晓莉

（1合肥工业大学土木与水利工程学院，合肥230009）（2武汉大学卫星导航定位技术中心，武汉430079）（3安徽省北斗卫星导航重点实验室，合肥230088）

1 引言

1997年，美国喷气推进实验室（JPL）的Zumbeger等人提出了非差精密单点位方法（Precise Point Positioning，PPP）[1]。实时卫星轨道及卫星钟差的精度是影响实时PPP定位精度的重要因素。国际GNSS服务（International GNSS Service，IGS）于1994年GPS进入完全运行状态后开始提供GPS精密星历[2-3]。目前，IGS提供日常所有GPS卫星的高精度轨道与钟差[4]，其星历产品包括超快速星历产品、快速星历产品和最终产品3种[1，5]，所有IGS星历均以SP3格式[6]给出的。

IGS提供的卫星最终星历产品，卫星钟差的精度优于0.1ns，其精度完全能够满足厘米级的单点定位要求，但是这个产品要13天后才能获取，不能满足实时单点定位的要求。超快星历可以实时获取，但其卫星钟差在5ns左右，无法满足实时精密单点定位的精度要求。因此，实时获得较高精度的卫星钟差是实时精密单点定位的前提。

快速星历钟差精度与最终星历相当，但其时延只有17h，如果利用快速星历的钟差建模预报精密钟差，只要预报时间长度超过17h，即可获得实时钟差。但预报的前提是预报误差要小于外推星历的钟差。为了获得高精度预报结果，本文对卫星钟差的特点进行了研究，根据钟差特点首先提取趋势项部分，再根据频谱分析确定预报输入时间段长度与预报时段长度，然后采用RBF神经网络建模预报。这里采用RBF神经网络是因其具有学习速度快且可避免局部极小问题的优点。

2 钟差预报方法

2.1 趋势项提取

卫星钟差序列具有一定的趋势项，宜先将趋势项提取，然后再根据提取后的趋势项建模预报。根据文献[7]研究结果，宜采用多项式方法提取卫星钟差趋势项式，钟差趋势项建模多项式为

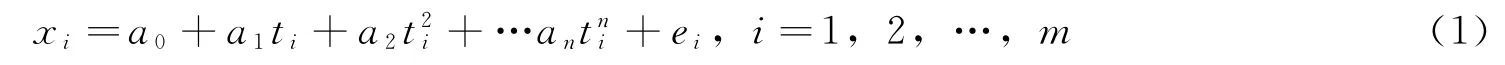
式中xi为钟差观测数据；ti为观测时间；an为待估计参数；ei为观测误差；m为观测总数；n为多项式次数，n的值要根据钟差数据的特点来确定。

当m＞n时，可根据最小二乘方法建模，求出待估计参数：

根据求出的参数，即可建立模型提取钟差的趋势项。

2.2 频谱分析

对于提取趋势项后的钟差数据，要进行短期预报。首先需要确定建模数据长度与预报时间长度。这需要对钟差数据的规律进行研究，特别要研究其周期性。本文研究的是短期预报，所以要研究短期钟差数据的周期变化特征，也就是频率域上的特征，这里选用离散傅里叶分析方法。

假设观测值时间序列为f（kΔt），k＝0，1，…，N-1，Δt为时间间隔，时间长度为T，则T＝NΔt。取频率间隔Δf＝1／T，令j＝0，1，…，N-1，则相应的离散傅里叶变换为

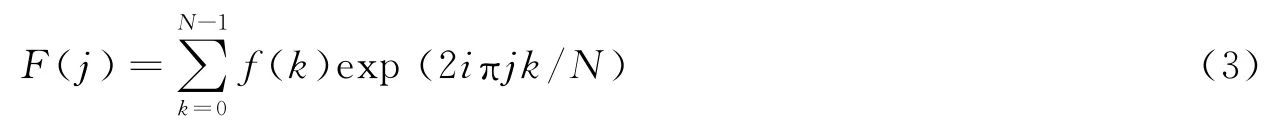
2.3 RBF神经网络

根据离散傅里叶分析了解钟差数据的周期性特征之后，可以确定建模周期与预报时间长度。由于提取趋势项后的数据具有非线性特征，采用RBF神经网络建模预报是因其具有逼近非线性函数能力强和网络收敛速度快的优点。

RBF网络是一种三层前向网络[8]。输入层由信号源结点组成。第二层为隐含层，第三层为输出层，它对输入模式的作用做出响应。

由输入层、隐含层和输出层构成的一般径向基神经网络结构如图1所示。

RBF网络的关键在于隐含层节点径向基函数的非线性逼近性能，一般采用的RBF函数是高斯分布函数，则隐含层节点k的传递函数表达式为

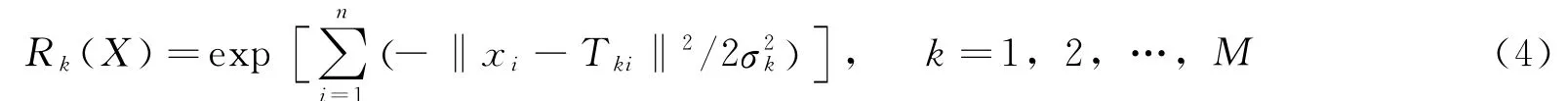
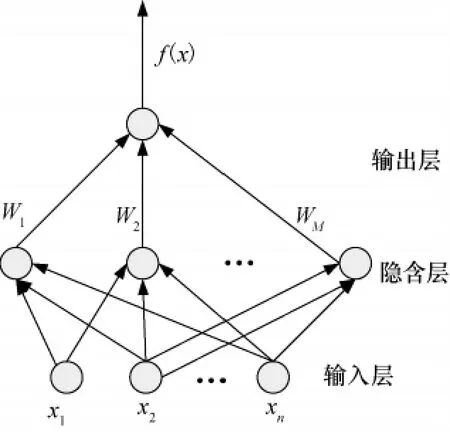
图1 RBF神经网络结构Fig.1 Structure of RBF neural network

式中X＝（xi｜i＝1，2，…，n），n为输入向量维数；Tki为节点K的中心Tk的第i个分量；σk为节点k的高斯分布宽度；‖·‖表示欧式范数。

输出层节点相应的输出则可以表示为

式中ωk为权值。分两个阶段来训练RBF网络：第一步是决定隐含层神经元的数量M，以及决定每个神经元的高斯函数的宽度σk和中心点Tk；第二步是使用训练数据根据全局误差准则来训练权值ωk，使RBF网络拟合训练数据最佳。

3 钟差试验与结果分析

本文建模预报精密钟差，首先要保证预报精度，其次要保证预报时间大于17h，同时要适用于不同类型的卫星。

采用IGS提供的5min间隔快速星历的钟差，本文研究的是短期预报，分析的对象是2d的钟差数据。选择2d的5min间隔的超快速（实测）钟差数据，先对其中丢失的数据进行插值补全，然后采用离散傅里叶分析对钟差数据进行频谱分析。根据卫星钟差类型和特点，选择具有代表性的BLOCK Ⅱ／ⅡA Cs钟PRN 09，BLOCK Ⅱ／ⅡA Rb钟PRN 05，BLOCK Ⅱ／ⅡF Cs钟PRN16。

这里先以PRN05为例，选择2011-08-23T0：0：0.00000000—2012-08-24T23：0：45.000 000 00两天快速钟差数据，如图2所示。

由图2可以看出短期内快速钟差呈现线性趋势，因此采用线性函数（一次多项式）提取钟差的趋势项部分，提取趋势项后的钟差如图3（a）所示。对提取趋势项后的钟差数据进行快速傅里叶分析，其结果如图3（b）所示。

从图3（b）可以看出，频谱分析的尖峰在24h（每天1周期）与12h（每天两周期）。这是由于卫星钟差的变化受到日照、温度与环境等影响，而这些因素受到卫星运动影响。卫星运动的周期为11.965 9h，因此卫星钟差变化的周期与之相对应。因此，本文选用24h钟差数据，先提取趋势项，再利用提取趋势项后的钟差数据建模，短期预报24h钟差，再加上趋势项，得到24h预报钟差。从图3（a）可以看出，提取趋势项后的钟差规律不明显，选用RBF神经网络对其建模预报。

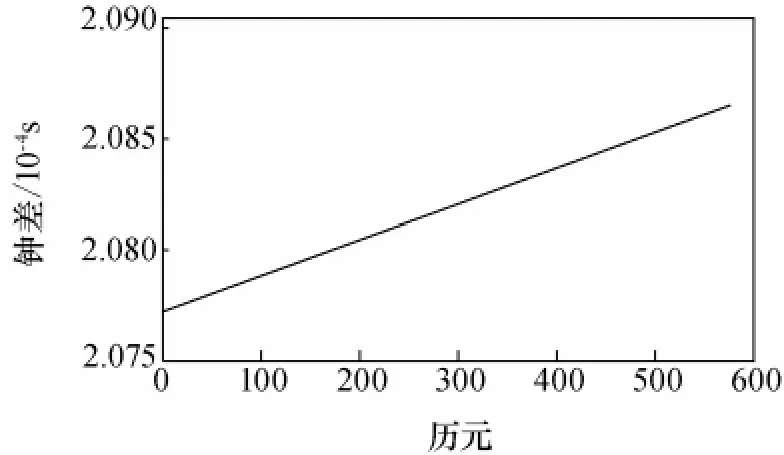
图2 PRN05连续两天钟差图Fig.2 Two continuous days′clock error of PRN05

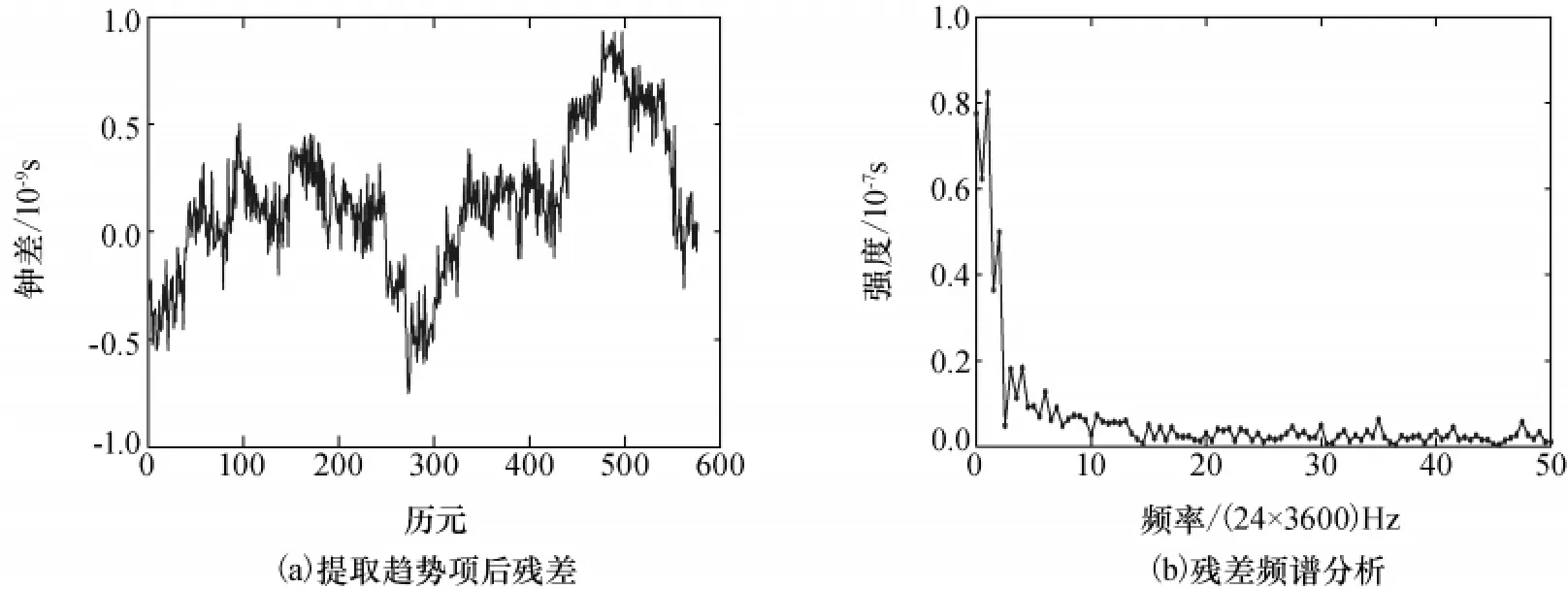
图3 趋势项提取及频谱分析Fig.3 Trend extraction and spectrum analysis

选择2011-08-23T0：0：0.00000000—2012-08-23T23：0：45.000 000 00一天快速钟差数据，经过上述的方法提取趋势项，再利用提取趋势项后的支持数据作为输入，训练RBF神经网络。RBF神经网络训练样本输出与实际样本之间的差值如图4所示。

由图4可以看出，训练误差的均值为0.115 2ns，标准差为0.144ns，而快速钟差的精度是0.2ns，训练时设定的条件就是高于0.2ns就停止训练。

利用训练好的RBF神经网络，对2011-08-23T0：0：0.00000000—2012-08-23T23：0：45.000 000 00一天的钟差数据进行预报，预报后的数据再加上趋势项，得到最终的预报钟差，预报钟差与实际钟差之间的差值（预报误差）如图5所示。

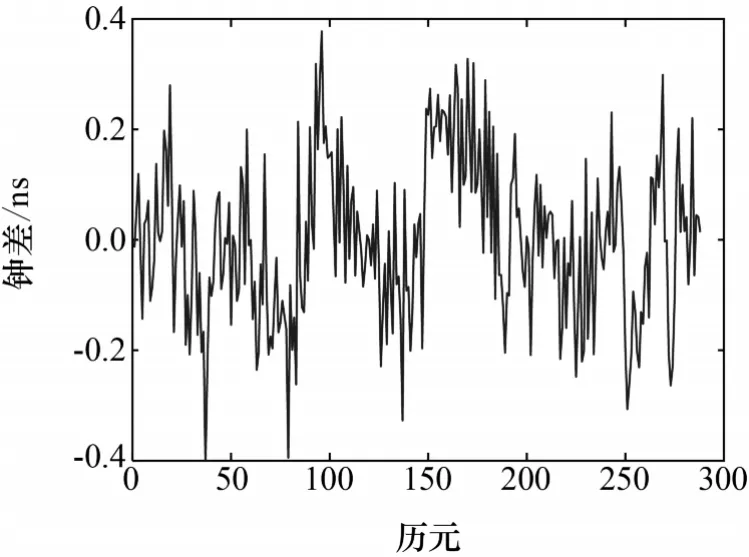
图4 训练误差Fig.4 Training error

图5 预报误差Fig.5 Prediction error

由图5可以看出，预报误差的均值为0.266 7ns，标准差为0.215 3ns，最大误差为0.809 1ns，而超快星历（外推）钟差的精度是5ns，预报星历钟差的精度远高于超快星历（外推）钟差，可以满足厘米级实时定位需求。

采用同样的方法对BLOCKⅡ／ⅡA Cs钟PRN 09，BLOCKⅡ／ⅡF Cs钟PRN 16的快速星历钟差数据进行预报，可得到类似的精度，限于篇幅，不一一列出。

4 结束语

本文利用IGS快速星历的GPS卫星钟差建模进行短期预报，其目的是能够得到高精度的实时卫星钟差，其预报时间段长度必须要大于快速星历的时间延迟，其精度要高于超快速星历。对卫星钟差提取趋势项有利于建模预测，短期卫星钟差的周期性特征识别有利于确定建模时间段长度与预报时间段长度，利用RBF神经网络建模预报效果良好。本文预报方法能够得到实时卫星钟差，其精度在1ns以下，可以用于分米级甚至更高精度的导航定位。然而，本文仅仅从过去的观测序列本身建立模型实施预报，如果能结合原子钟运行的物理特性，可使预报更加完善。

[1]ZUMBERGE J，HEFLIN M，et al.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J].Journal of Geophysical Research，1997，102（B3）：5005-5017.

[2]OLIVER MONTENBRUCK，EBERHARD GILL，REMCO KROES.Rapid orbit determination of LEO satellites using IGS clock and ephemeris products [J].GPS Solutions，2005（9）：226-235.

[3]KOUBA J.A guide to using international GPS service （IGS）products.A Guide to Using International GPS Service（IGS）Products [EB／OL]. [2009-04-30].http：∥igscb.jpl.nasa.gov／igscb／resource／pubs／GuidetoUsingIGSProducts.pdf.

[4]BERNHARD HOFMANN-WELLENHOF，HERBERT LICHTENEGGER，ELMAR WASLE.GNSS-Global Positioning Satellite Systems GPS，GLONASS，Galileo＆more[M].New York：Springer-Verlag，2008：46-51.

[5]FANG P，GENDT G，SPRINGER T，et al.IGS near real-time products and their applications[J].GPS Solutions，2001（4）：2.

[6]MONTENBRUCK O，GILL E，KROES R.Rapid orbit determination of LEO satellites using IGS clock and ephemeris products [J].GPS Solution，2005（9）：226-235.

[7]KENNETH L SENIOR，JIM R RAY，RONALD L.Beard characterization of periodic variations in the GPS satellite clocks [J].GPS Solutions，2008（12）：211-225.

[8]HINT K J.Extending the Functional Equivalence of Radial Basis Function Network and Fuzzy Inference System [J].IEEE Translation on Neural Networks，1996（3）：776-781.