基于分数阶滑模的航天器姿态鲁棒控制

邓立为 宋申民

（哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨150001）

1 引言

伴随着航天器编队飞行、空间交会对接、在轨服务等技术的发展，高精度高稳定度的航天器姿态控制要求越来越高，而航天器的姿态控制系统具有非线性、强耦合、多入多出等特点，诸如重力梯度、太阳辐压、地球磁场等各种环境干扰力矩都是无法精确描述的，并且航天器的转动惯量信息也是无法精确得到的，所以具有良好鲁棒性与抗干扰性的非线性控制器得到了广泛重视。滑模变结构控制由于对模型误差和外部扰动具有较好的鲁棒性，因此在航天器的姿态控制系统中得到了广泛的应用。文献［1］研究了非线性系统的模糊分数阶滑模控制问题，分别给出了PD型滑模面和PDα型滑模面，对比说明分数阶滑模控制的优点，但没有给出收敛到滑模面之后状态的收敛性证明。文献［2］利用分数阶非奇异终端滑模研究了非自治混沌系统的同步与有限时间控制问题。文献［3］研究了一类具有不确定性分数阶动力学系统的分数阶终端滑模控制问题，对集成不确定部分的分数阶微分的界做出了一定的假设。文献［4］通过滑模控制研究了整数阶混沌系统与一类分数阶混沌系统之间的同步问题。文献［5］基于参数自整定分数阶滑模对交流永磁伺服电动机的速度控制进行了研究。但是，上述研究中控制对象、假设条件的特殊性以及证明的不完整性，使得研究成果并不能简单地直接应用到航天器的姿态控制问题上。本文以航天器存在转动惯量不确定性与外部扰动为前提，利用分数阶滑模控制理论对航天器姿态实现高精度和高稳定度控制，并给出了相关的稳定性证明。最后，通过仿真验证了所提出的分数阶滑模控制器具有高精度、强鲁棒性和良好的抗干扰性。

2 基础理论

定义1 连续可积函数ft（）的Caputo型分数阶微积分统一定义为［6-7］

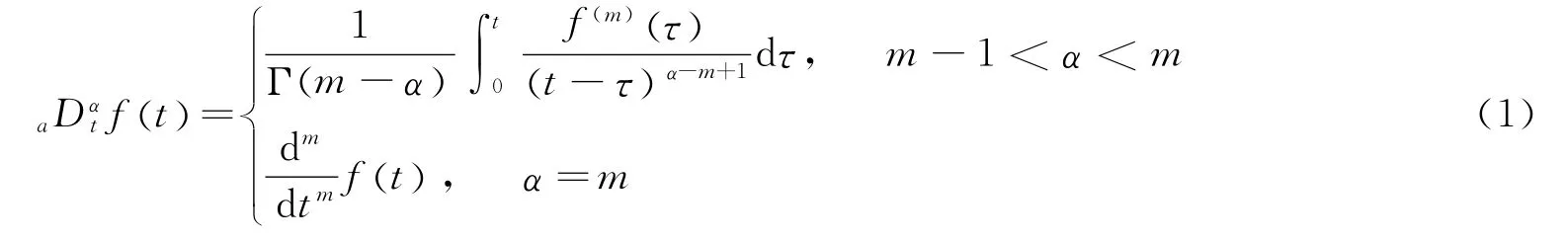
式中m为比α大的最小整数；Γ·（）为伽马函数，时，符号表示分数阶微分；而当α＜0，则表示分数阶积分。分数阶微分运算转化为特定形式的积分运算，因而具有一定的记忆性。为表述方便，下文用符号

分数阶微积分具有如下性质［3，6］：

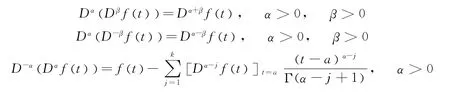
3 航天器的姿态运动学与动力学

3.1 航天器的运动学方程

修正的罗德里格参数（Modified Rodrigues Parameters，MRPs）描述的航天器运动学方程为［8］

式中σ为本体坐标系相对于惯性坐标系的MRPs参数描述，其定义为σ＝etan（θ／4）（0°≤θ＜360°），θ为Euler旋转角，e为Euler旋转轴；是本体坐标系相对于惯性坐标系，表示在航天器本体坐标系上的姿态角速度矢量；Gσ（）具有如下形式的定义：

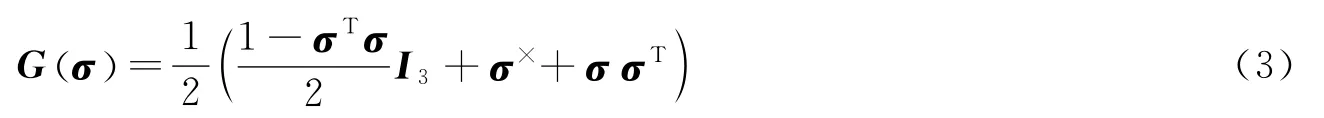
并且，Gσ（）具有如下性质：

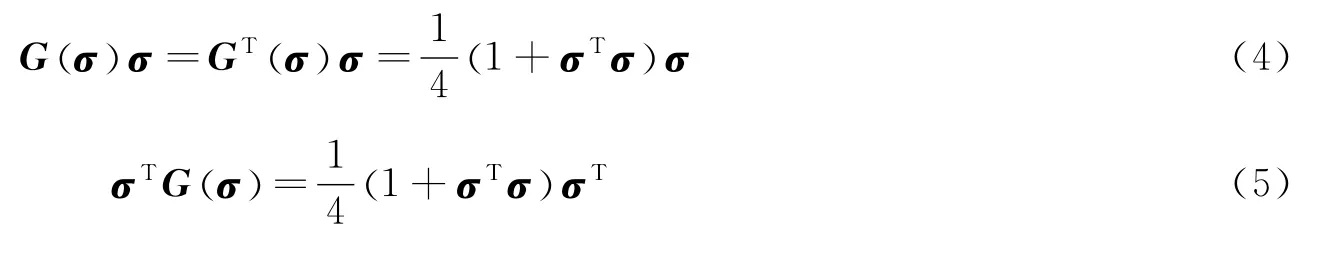
3.2 航天器的动力学方程

刚体航天器的动力学方程为［8-9］

式中J∈R3×3为航天器的对称正定转动惯量矩阵为航天器本体坐标系上的三轴控制力矩，可以由航天器上的反作用飞轮、推力器和磁力矩器等执行机构提供；为航天器所受的干扰力矩；对于符号ω×表示如下的反对称矩阵：

航天器姿态控制问题描述：针对由式（2）和式（6）组成的刚体航天器姿态控制系统，设计控制器u，使得当t→∞时，系统的姿态信息σ→0以及角速度信息ω→0。

4 分数阶滑模控制器设计

为了便于本文分数阶滑模控制器的设计，对上述运动学与动力学方程进行变形，得到它们的等价方程。引入新变量z，并定义为

对式（8）求导，并把得到的结果代入到式（6）中，从而得到关于新变量z的方程

针对由式（2）和式（9）组成的系统，设计分数阶滑模面为

设计相应的控制律为

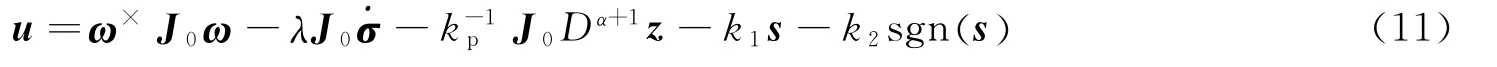
为了定理的证明，给出如下引理及假设：

引理1［9］对于一个连续系统假设存在一个连续的正定函数V：Rn→R，a∈R＋，β∈ （0，1），并且存在原点的一个邻域U0⊆Rn使得：

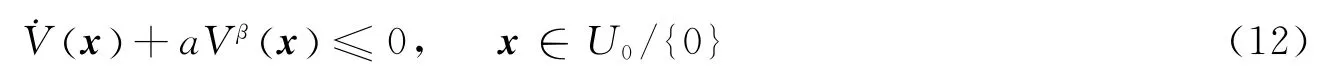
那么，原点就是一个平衡点，可在有限时间内到达。若U0＝Rn，那么原点就是一个有限时间内到达的全局平衡点。

引理2［5，7］分数阶非自治系统

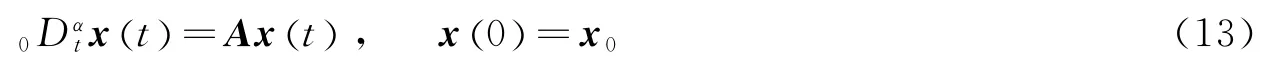
式中xt（）∈Rn；A＝（aij）∈Rn×n；0＜α＜1。当且仅当，

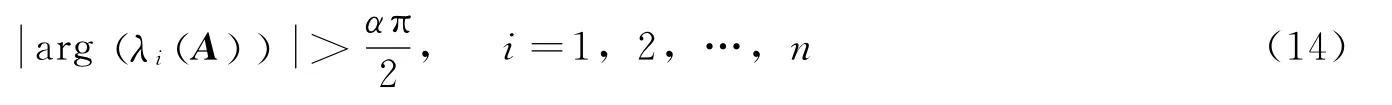
系统是渐近稳定的，并且状态元素向平衡点0的收敛速度是t-α；其中，arg表示辐角，λi表示矩阵的特征值。

假设1 存在已知常数dmax＞0，使得干扰力矩d满足约束条件：

假设2 存在已知常数ΔJmax＞0，使得转动不确定性部分满足约束条件：

定理 针对由式（2）和（9）组成的系统，通过选取由式（10）组成的分数阶滑模面，在控制律式（11）作用下，闭环系统的状态在有限时间内收敛到滑模面上，即s＝0。当t→∞时，系统的状态σ→0，ω→0。

证明过程分三部分完成：1）在有限时间内取得s＝0；2）当s＝0时，分数阶滑模面构成子系统状态变量z的收敛性；3）当z→0时，整个系统状态σ和ω的收敛性。

证明：

1）选取Lyapunov函数为

求V1对时间的一阶导数，并利用式（9）、式（10）以及式（11）可以得到：

利用矩阵范数之间的关系与二次型函数的性质可以得到：

最终可以得到：

应用引理1可知，系统有限时间内到达滑模面上。

上述证明过程中只给出了时变参数k2形如式（19）不等式关系，利用范数关系及式（15）和式（16），有：

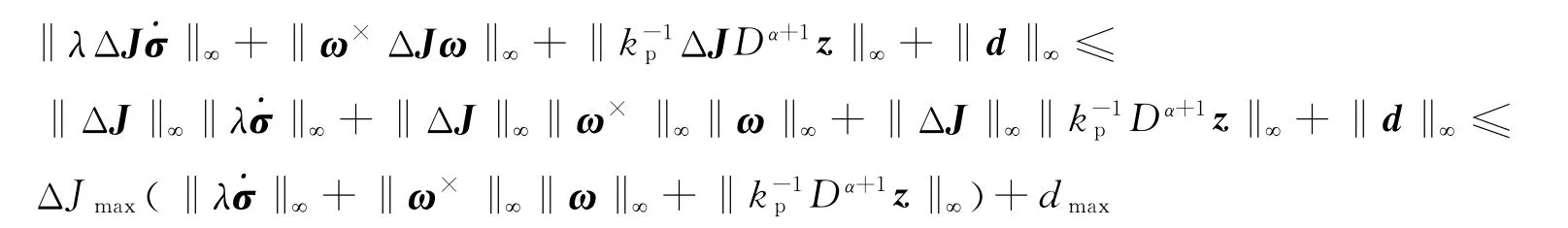
从而，可以选取时变参数k2：

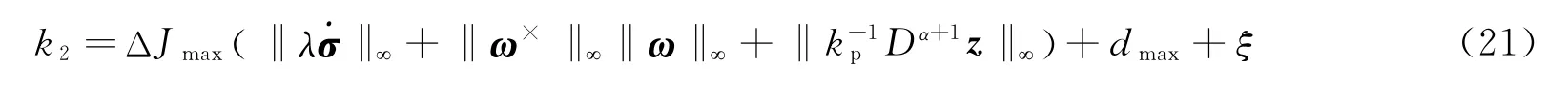
2）当s＝0时，子系统变为Dαz＝-kpz，是常见的分数阶系统。

由引理2可以得到：

由0＜α＜1和kp＞0可知，式（22）是恒成立的。从而可知，分数阶子系统Dαz＝-kpz是渐近稳定的，并且以t-α的速度向平衡点0处收敛。

3）当z→0，由方程ω＝-λσ可以得到，子系统方程为选取Lyapunov函数为

对函数V2求导，并利用式（2）和式（5），可以得到：

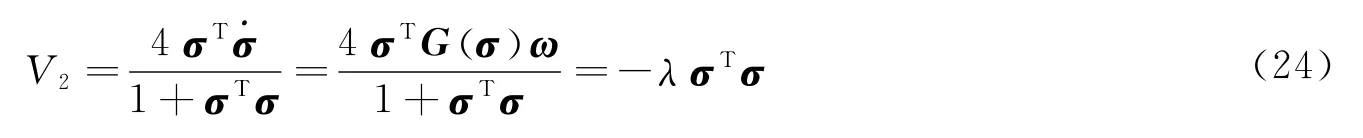
由Lyapunov稳定性定理可以得到，当t→∞时，σ→0，进而由方程ω＝ -λσ可以得到ω→0。

证毕。

在控制律式（11）中，因为符号函数的特性会引起系统控制力矩的抖振，抖振现象可能引起系统的不稳定或者对控制执行机构的损坏。为避免此问题，利用饱和函数对符号函数进行替换，其饱和函数sat·（）的定义为

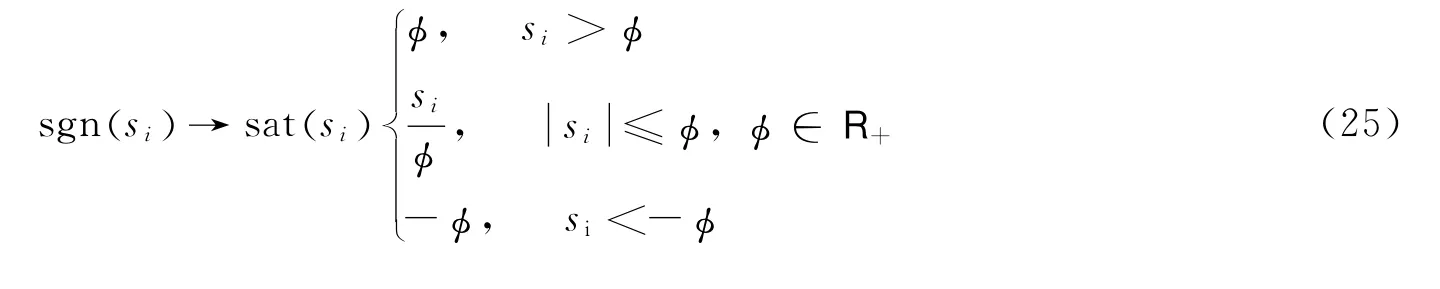
5 仿真分析

5.1 仿真参数设定

为了分析文中所提出的分数阶滑模控制律式（11）在高精度高稳定度的航天器姿态控制问题上的优势，选取文献［9］中的仿真参数。

航天器参数：

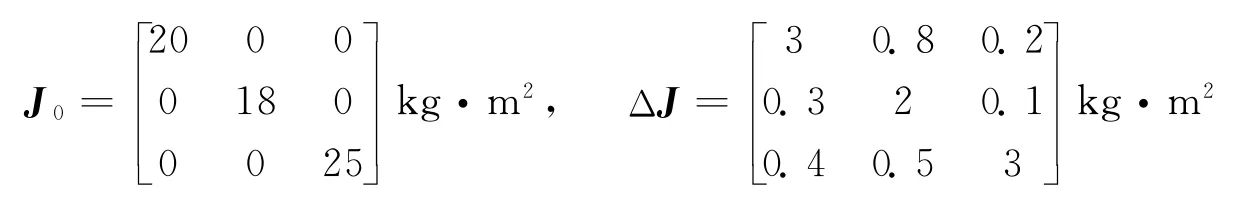
根据姿态四元数与姿态修正的罗德里格参数的转换关系可以得到，航天器初始姿态信息：

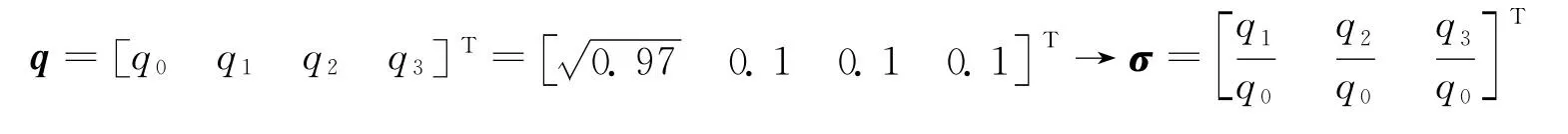
初始角速度信息为

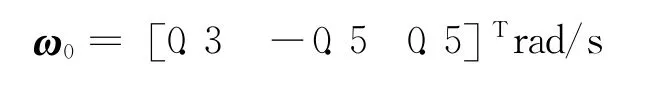
扰动力矩为

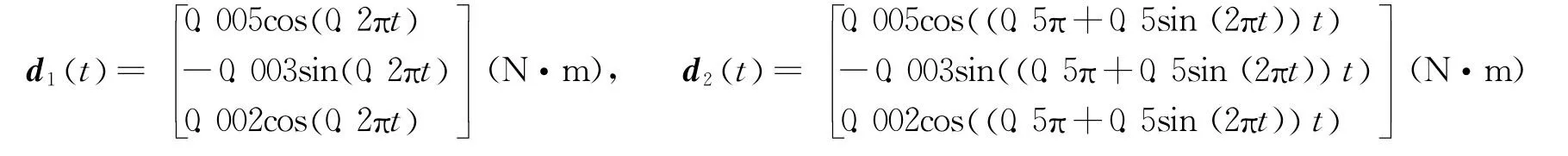
5.2 仿真结果分析

利用文中所提出的算法，采用上述仿真参数，并选择确定频率的干扰力矩d1t（）进行仿真，得到如下仿真结果：图1是文献［9］中有限时间控制器作用下的姿态及角速度曲线；图2是文献［9］中有限时间控制器作用下的滑模面与控制力矩曲线；图3是本文分数级滑模控制器作用下的姿态及角速度曲线；图4是本文分数级滑模控制器作用下的滑模面及控制力矩曲线；图5是时变参数k2的变化曲线。

图1 有限时间控制的姿态与角速度Fig.1 Attitude and angular velocity of finite time control

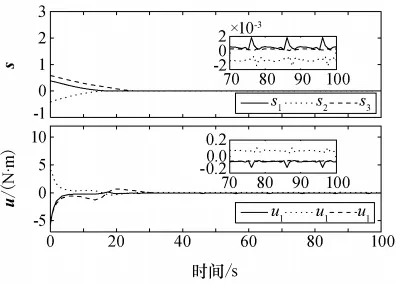
图2 有限时间控制的滑模面与控制力矩Fig.2 Sliding surface and control moment of finite time control

图3 分数阶滑模控制的姿态与角速度Fig.3 Attitude and angular velocity of fractional order sliding control

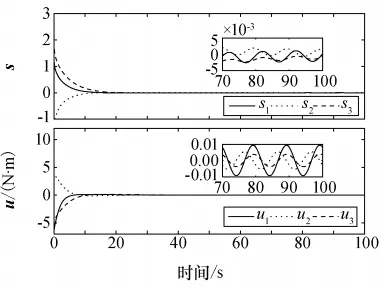
图4 分数阶滑模控制的滑模面与控制力矩Fig.4 Sliding surface and control moment of fractional order sliding control

从图1和图3对比可以看出，在存在转动惯量不确定与外部扰动的情况下，两种控制器作用下的姿态与角速度在35s左右均很好地完成了收敛。但是，分数阶滑模控制器作用下的航天器角速度收敛过程变化平缓，使得航天器姿态控制过程更加平稳。从图2和图4对比可以看出，航天器进入稳态阶段，分数阶滑模需要的控制力矩是0.005N·m，而文献［9］需要的控制力矩是0.1N·m。从图1～图4的局部放大图可以看出，分数阶滑模控制器在使用较小的控制力矩作用下，航天器姿态与角速度稳态精度更好，并大幅度提高了航天器的能源利用率。从图5时变参数k2的变化曲线可以看出，在姿态与角速度趋于0之后，根据式（21）可以得出k2＝ξ＋dmax＝0.9，仿真结果与理论分析相一致。

为了能够更好更直观地体现航天器的姿态信息，利用四元数、MRPs与Euler角之间的转换关系，将图1中四元数和图3中MRPs表示的姿态转化成欧拉角，得到如图6所示欧拉角表示的航天器姿态，图6上部分曲线表示文献［9］的姿态信息，图6下部分曲线表示本文分数阶滑模控制得到的姿态曲线。

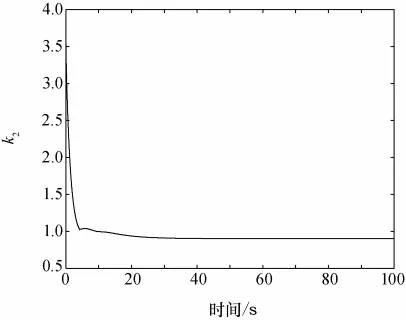
图5 时变参数k2变化Fig.5 Time-varying parameter k2

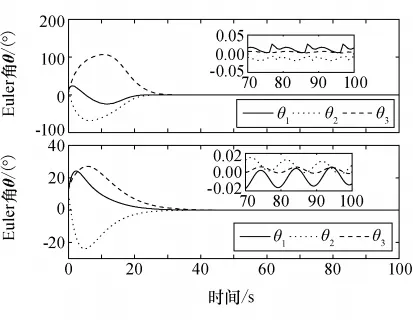
图6 欧拉角表示的航天器姿态Fig.6 Spacecraft attitude representation of Euler angles

从图6中可以看出，分数阶滑模控制器作用下的航天器，在调节过程中超调量小，在稳态阶段稳态误差小。

另一方面，诸如重力梯度、太阳辐压、地球磁场等各种环境干扰力矩的频率都是无法精确描述的，为了验证所设计的控制器在变频率干扰力矩下的控制效果，在上述仿真基础上，在不改变其他航天器参数及控制器参数的前提下，采用5.1节中的变频率扰动力矩d2t（）再次进行仿真，得到如下结果：图7是文献［9］中有限时间控制器作用下的姿态及角速度曲线；图8是分数级滑模控制器作用下的姿态及角速度曲线。

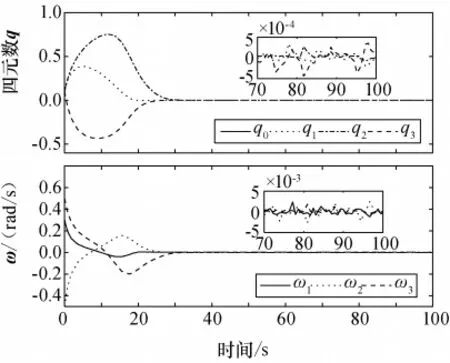
图7 有限时间控制的姿态与角速度Fig.7 Attitude and angular velocity of finite time contol

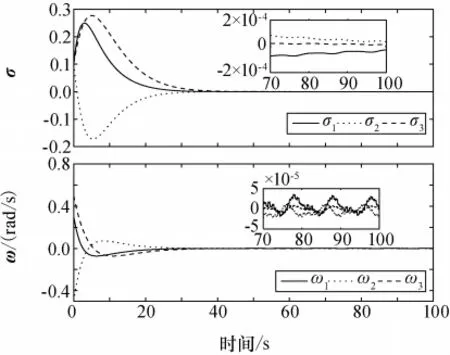
图8 分数阶滑模控制的姿态与角速度Fig.8 Sliding surface and control moment of fractional order sliding control

从图7、图8可以看出，在变频率干扰力矩条件下，两种控制器都能完成对航天器的精确控制。在调节过程中，收敛速度与确定性频率干扰下的收敛速度一样；在稳态阶段，分数阶滑模控制器与文献［9］控制器相比，具有更小的稳态误差4×10-5rad／s。

6 结束语

针对存在外部扰动及转动惯量不确定性的高精度高稳定度的航天器姿态控制问题，将分数阶微分算子的快速收敛性和记忆性与滑模控制器优点结合起来，提出了一种分数阶滑模控制器。并利用Lyapunov理论与分数阶稳定性理论分三部分完成了整个系统的稳定性证明。MATLAB仿真表明所提出的分数阶滑模控制器具有良好的控制性与强鲁棒性。并针对变频率扰动干扰力矩问题，仿真分析了分数阶滑模控制器的良好抗干扰性。

本文所设计的控制律仅能使得到达滑模面的时间是有限的，而在滑模面上系统是渐近稳定的，如果能设计有限时间收敛性能的滑模面子系统，将能使整体系统达到有限时间稳定，从而实现有限时间收敛的分数阶滑模控制器。另外，进一步结合文献中的自适应理论与扰动观测器的设计方法，将能够减少控制器设计过程中对扰动以及不确定性界的要求，从而使得航天器的分数阶滑模方法更具有工程意义。以上两点是以后课题研究的重点。

［1］DELAVARI H，GHADERI R，RANJBAR A，et al.Fuzzy fractional order sliding mode controller for nonlinear systems ［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15（4）：963-978.

［2］AGHABABA M P.Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic（hyperchaotic）systems using fractional nonsingular terminal sliding mode technique ［J］.Nonlinear Dynamics，2012，69（1）：247-261.

［3］DADRAS S，MOMENI H R.Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty ［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17（1）：367-377.

［4］CHEN D Y，ZHANG R，SPROTT J C，et al.Synchronization between integer-order chaotic systems and a class of fractional-order chaotic system based on fuzzy sliding mode control［J］.Nonlinear Dynamics，2012，70（2）：1549-1561.

［5］ZHANG B T，PI Y G，LUO Y.Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor［J］.ISA Transactions，2012，51：649-656.

［6］MONJE C A，CHEN Y Q，VINAGRE B M，et al.Fractional-order systems and controls fundamentals and applications［M］.London：Springer，2010.

［7］PODLUBNY I.Fractional differential equations［M］.San Diego：Academic press，1999.

［8］SONG S M，ZHANG B Q，WEI X Q，et al.Asymptotical stability analysis of"PD＋"controller for spacecraft attitude tracking system ［C］.8th World Congress on Intelligent Control and Automation，July 7-9，2010，Jinan，China，2010：3908-3913.

［9］TIWARI P M，JANARDHANAN S，NABI M U.A finite-time convergent continuous time sliding mode controller for spacecraft attitude control［C］.11th International Workshop on Variable Structure Systems，June 26-28，2010，Mexico City，Mexico，2010：399-403.