用杆臂效应在轨标定加速度计标度因数的方法

党建军 罗建军 万彦辉

（1西北工业大学航天学院，西安710072）（2西安精密机电研究所，西安710100）

1 引言

惯性器件在地面条件下和空间飞行条件下的漂移率有很大差别，而且当受空间环境振动、辐照等影响，其性能会退化，导致参数变化。加速度计作为惯性导航的核心器件，其测量量本身包含零位误差、标度因数误差及安装误差［1］。加速度计误差系数地面标定通常是在转台或分度头上利用重力加速度进行标定，因而标定工作只能在实验室进行［2］。考虑到加速度计误差系数随温度和时间变化，仅在地面标定的加速度计误差系数是不能准确反映加速度计真实偏差的。地面标定只能作为加速度计误差系数的参考值，对自主导航精度要求不严的航天器比较适用，但对于自主导航要求加速度计测量信息较高的航天器就不再适用。如不考虑这些误差将会对自主导航产生严重误差。为保证空间自主导航的精度，需要对加速度计的误差系数进行在轨标定［3］。

国内外诸多学者对GRACE卫星等所使用的加速度计标定提出了多种方法［4］。目前对加速度计进行在轨标定可以归结为以下几种途径：用重力场模型反演加速度计参数［5］；用轨道的精确数据推导加速度计的参数；根据发动机的推力来标定加速度计的参数；利用能量守恒方法进行标定［6］。这些方法一般考虑同时标定加速度计零位偏差和标度因数误差，固定一个参数，解算另一个参数，存在较大的耦合作用，且算法复杂，有时不能满足对加速度计标定精度要求较高的需求；或者需要其他设备辅助、成本较高、精度差，且工程上难于实现。

本文提出了一种利用杆臂效应在轨标定加速度计标度因数的方法，该方法将3块加速度计正交安装于两轴旋锁机构。旋锁机构旋转时加速度计会产生杆臂效应，利用杆臂效应产生的加速度即可标定出加速度计的标度因数。

2 加速度计误差模型

2.1 在轨标定常用坐标系及其定义

（1）地心惯性坐标系Oi-XiYiZi（简称i系）

坐标原点为地球质心Oi，基本平面为地球平赤道面；Xi轴在基本平面内指向春分点；Zi轴 垂直于天赤道面指向北极；Yi轴在赤道面上垂直于Xi轴，且与Xi轴和Zi轴组成右手直角坐标系。

（2）轨道坐标系Oo-XoYoZo（简称o系）

航天器轨道平面为坐标平面，其中，航天器的质心为原点Oo；Zo轴由航天器质心指向地心；Xo轴在轨道平面内与Zo轴垂直并指向航天器速度方向：Yo轴与Xo、Zo轴右手正交且与轨道平面的法线平行。

（3）惯组本体坐标系Ot-XtYtZt（简称t系）

该坐标系为惯组的安装坐标系，与转台内框固联。

（4）导航坐标系Oo-XnYnZn（简称n系）

导航坐标系是在导航时根据导航系统工作原理选取的作为导航基准的坐标系。本文中选取的导航坐标系为地心惯性坐标系。

（5）航天器载体坐标系Oo-XbYbZb（简称b系）

航天器载体坐标系是固连在卫星体上的坐标系。载体坐标系的坐标原点位于航天器的质心Oo，当转台处于零位时载体坐标系与惯组本体坐标系重合。

2.2 加速度计误差模型

捷联惯组上通常正交安装有3块加速度计，其误差模型如下［7］：

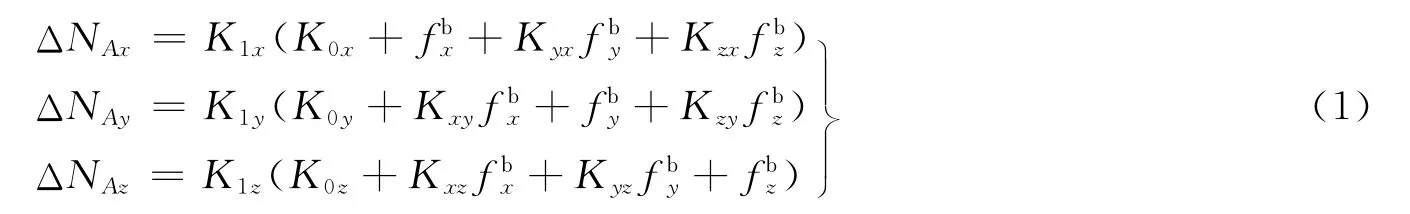
式中 ΔNAx，ΔNAy，ΔNAz分别为3个加速度计单位时间内输出的脉冲数；分别为3个方向在b系的相对加速度；K0x，K0y，K0z分别为3个加速度计偏值；K1x，K1y，K1z分别为3个加速度计输出的标度因数；Kyx，Kzx，Kxy，Kzy，Kxz，Kyz为加速度计的安装误差系数。

3 杆臂效应分析

捷联惯组理论上应安装在飞行器的质量中心，且惯性测量部件的本身尺寸也为零。但实际上惯性测量部件的安装基座会偏离飞行器质心一定距离，且本身尺寸也不可能为零，由于存在切向加速度和向心加速度，会引起加速度计的测量误差，这种现象为 “杆臂效应”［8-10］。

地心惯性坐标系Oi-XiYiZi和航天器载体坐标系Oo-XbYbZb如图1所示，惯性元件安装在载体坐标系中的p点处，Oo为航天器的质量中心，lp为加速度计偏离飞行器质心的距离，则加速度计所处位置的比力和航天器质心处的比力关系为

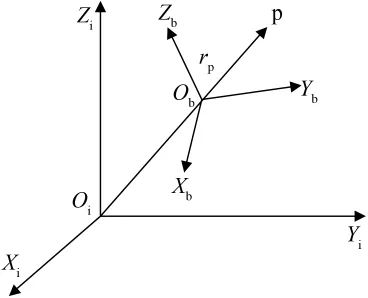
图1 杆臂效应示意Fig.1 Lever arm effect diagram

由于：

式中 （·）i表示相对惯性坐标系求微分；（·）b表示相对载体坐标系求微分；为载体坐标系相对于惯性坐标系的运动角速度。

则

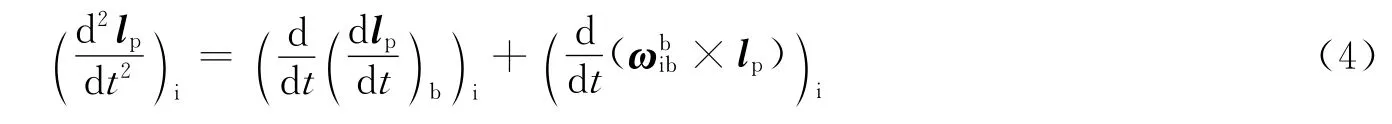
而

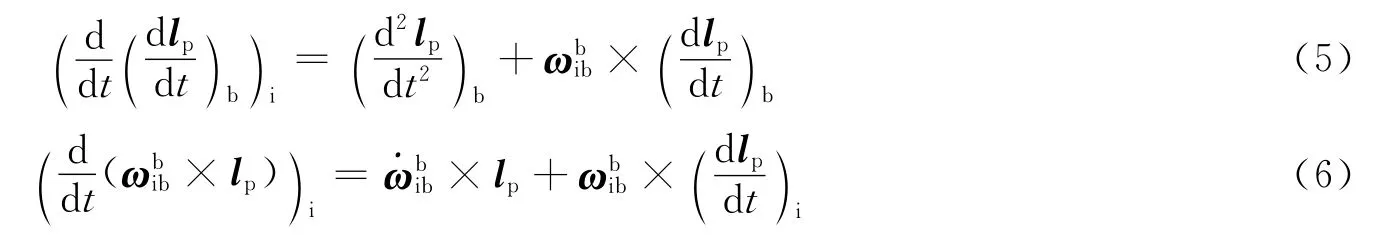
将式（3）代入式（6），得：

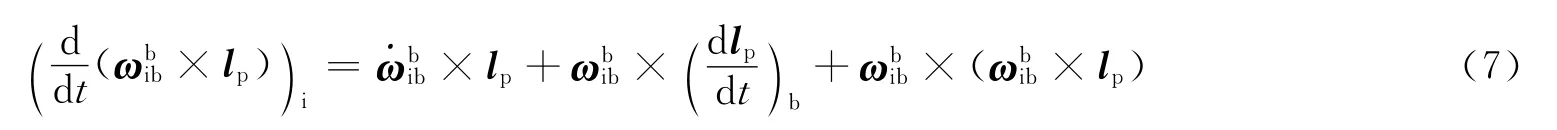
将式（5）和式（6）代入式（4），得：

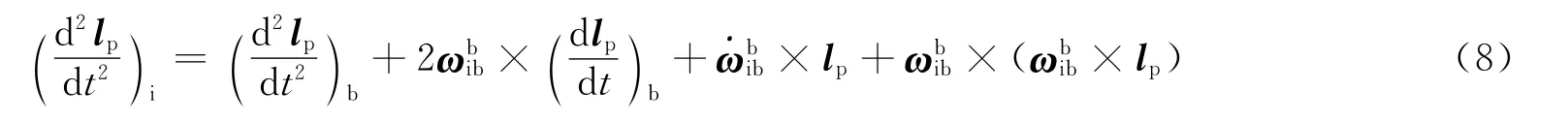
由于惯性测量组件的安装点p在载体坐标系中是固定的，故：

将式（8）代入式（2），有：

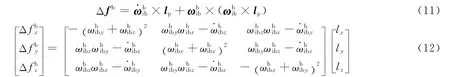
式（12）即为杆臂效应测量误差表达式，表征其会引起的导航参数误差。

4 加速度计标度因数标定方法

在进行加速度计标度因数标定前，先利用轨控前的恒星定向模式下加速度为零的特点标定出加速度计零位偏差。同时由于捷联惯导与航天器固联，因此本文认为加速度计安装误差系数保持稳定，采用地面实验室的标定值。另外，本文的标定也是在恒星定向模式下进行的，并且由于标定持续时间短，因此认为标定前后各种摄动力不发生变化。

航天器的姿态角分别为：航向角φ、俯仰角θ、横滚角γ。当旋锁机构未旋转时，惯组本体坐标系O-XTYTZT与航天器载体坐标系Oo-XbYbZb重合。假设旋锁机构绕OXT轴以ω匀速选转，则φ＝φ0＋ωt，φ0可为任意值。则航天器载体坐标系与惯组本体坐标系之间的转换矩阵为

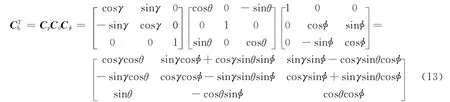
因此，

lx，ly，lz在惯组设计时就已经确定，因此，根据式（12）可以计算出

由式（1）有：

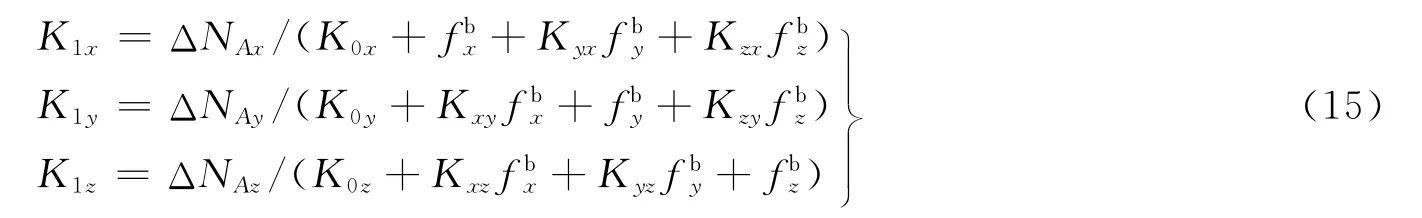
根据式（15）就可以分离出加速度计标度因数K1x，K1y，K1z。

当OXT轴以ω匀速旋转时，由式（12）可知输出很小，在此过程中分离出的K1x精度有限。因此，在完成旋锁机构绕OXT轴以ω匀速旋转后，再绕OYT轴以ω匀速旋转，两次旋转即可以较高的精度完全分离出加速度计标度因数K1x，K1y，K1z。

5 地面验证试验

为了验证本文提出的方法的可行性，在地面进行了相关试验。将惯组固定在转台上，并使加速度计的安装中心与转台轴心偏离一定的距离并精确测量该距离。

5.1 试验过程

标定使用的惯组K0x＝5.0×10-6gn，K0y＝4.0×10-6gn，K0z＝2.0×10-5gn；安装误差均在20角秒内，惯组陀螺的随机漂移精度在0.01（°）／h以内。惯组分别绕X轴及Y轴以10（°）／s、20（°）／s旋转一周，记录陀螺及加速度计的输出，并通过计算机精确计算出旋转时间。试验过程中加速度计及陀螺仪的输出分别见表1及表2。

5.2 试验数据处理方法

根据表1、表2中加速度计及陀螺的输出，由式（15）即可计算出加速度计的标度因数。用两个轴的一次旋转即可标定出加速度计的2个标定值。为了提高标定精度，在试验过程中分别绕X轴及Y轴以10（°）／s、20（°）／s各旋转一周，因此可以得到每个加速度计的4个标度因数值。由于每个轴、每个速率档的外部条件不同，因此可以取不同的加权系数。即

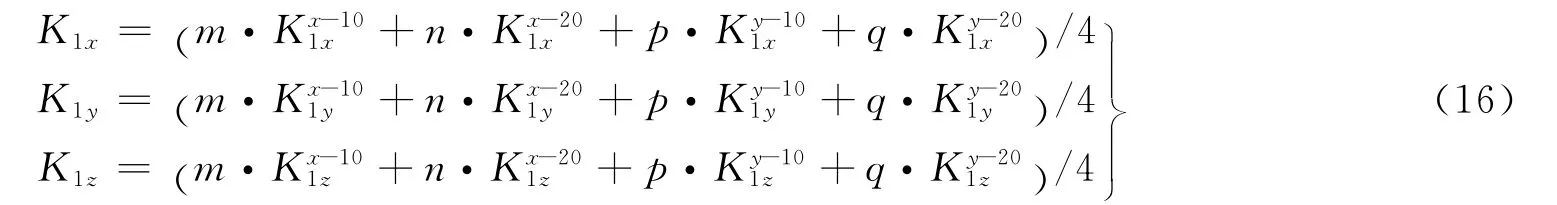
计算K1x，K1y，K1z时可根据具体情况分别取不同的加权系数，一般在大角速率旋转时加权系数大。如计算K1x时可取：m＝0.1，n＝0.4，p＝0.3，q＝0.2。

5.3 试验结果

根据表1、表2的输出，用式（15）、式（16）可以得到3个加速度计的标度因数。试验结果如表3所示。表3中的真实值为在地面实验室通过标准平板和分度头标定的加速度计标度因数（本文认定实验室标定结果为真实值），表3中标定误差为标定值与真实值的相对误差。表3的试验数据表明，利用杆臂效应能以较高精度标定出加速度计的标度因数。

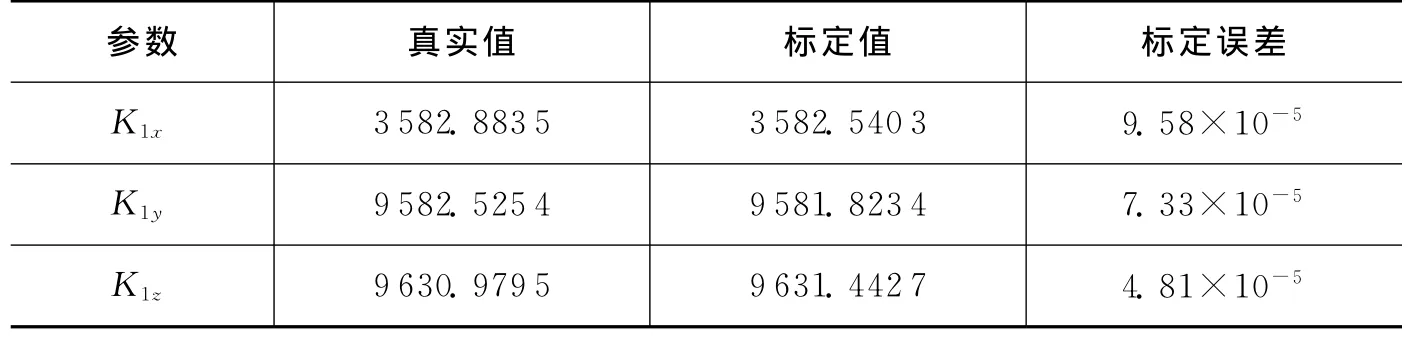
表3 加速度计标定结果Tab.3 Calibration result of the accelerometer 脉冲／（s·gn）

6 结束语

本文建立了加速度计的误差模型，分析了杆臂效应的原理，提出了利用杆臂效应的原理在轨标定加速度计标度因数的方法，详细推导了标定模型公式。进行了地面验证试验，给出了试验数据处理方法。地面验证试验表明，该方法标定精度较高，可用于加速度计的在轨标定。该在轨标定方法易于工程实现，不需其他辅助设备，完全自主标定，适合于加速度计的在轨标定。

［1］陈哲.捷联惯导系统原理 ［M］.北京：宇航出版社，1986：20-27.CHEN ZHE.Principle of SINS［M］.Beijing：The Astrionics Press，1986：20-27.

［2］HU ZHONGKUN，LUO JUN，WANGWENMIN.Optimum configuration of determining the gravitational constant G with four attracting masses［J］.International Journal of Modern Physics，2002，11（6）：913-920.

［3］RAMAN K V.Multiple approaches for gyro calibration of intelsat satellites ［J］.Advances in the Astronautical Sciences，2000，3（103）：2039-2053.

［4］BAR ITZHACK.Comparison Between Implicit and Explicit Spacecraft Gyro Calibration ［J］.WSEAS Transactions on Circuits and Systems，2003，2（4）：728-734.

［5］WANG F R.Study on center of mass calibration and K-band ranging system calibration of the GRACE mission ［D］.Austin：University of Texas，2003.

［6］VISSER P，SNEEUW N，GERLANCH C.Energy Integral Method for Gravity Field Determination from Satellite Oribit Coordinates［J］.Journal of Geodesy，2003（77）：207-216.

［7］党建军，罗建军.基于单轴速率转台的捷联惯测组合标定方法研究 ［J］.航空学报，2010，31（4）：806-811.DANG JIANJUN，LUO JIANJUN.Research on Calibration Method of SIMU Based on Single-axis Rate Turntable［J］.ACTA AERONAUTICA ET ASTRONAUTICA SINICA，2010，31（4）：806-811.

［8］JEON C W，KIM H J，LEE J G.An LS-TLS-based sequential identification algorithm application to an accelerometer［J］.IEEE Trans.on Aerospace and Electronic Systems，2001，37（2）：607-618.

［9］L QIN，L LI.Error Analysis and Compensation of Strapdown Inertial Navigation System ［J］.Journal of Beijing Institute of Technology，2002，11（2）：117-120.

［10］H XIUFENG.Analysis of Lever Arm Effects in GPS／IMU Integration System ［J］.Transaction of Nanjing University of Aeronautics ＆ Astronautics，2002，19（1）：59-63.