精确动力学模型中的行星引力辅助轨道设计

杨洪伟 陈杨 宝音贺西 李俊峰

（清华大学航天航空学院，北京 100084）

1 引言

在深空探测任务中，往往需要通过行星引力辅助来达到减少燃料消耗的目的。在利用行星引力辅助的深空探测任务分析与初步轨道设计中，通常采用等效脉冲引力辅助模型（下文简称“简化模型”），将行星引力辅助效果看作是一个瞬时的速度脉冲［1］，通过圆锥曲线拼接技术［2］设计轨道。但是在实际情况下，引力辅助是连续的过程：航天器在行星影响球内飞行需要一定的时间，飞行的过程中会受到太阳和其他行星的引力等摄动，并且这段时间内行星的位置速度会发生变化。这些因素会导致引力辅助结束时刻航天器实际的状态量与简化模型中不同。而引力辅助结束后航天器还要长时间的飞行，初始时刻状态量很小的不同就能引起终端时刻很大的响应，因此在实际的工程应用中必须采用精确的引力辅助模型设计深空探测器飞行轨道。此外，现在大多数研究都是基于简化模型，通过精确模型和简化模型计算结果对比可以验证简化模型的准确性和可信度。

针对精确动力学模型中的引力辅助轨道设计问题，文献［3］给出了在简化引力辅助模型基础上引入行星摄动设计精确轨道的方法，但是其方法存在影响球内外引力摄动不连续问题并且过程复杂。为了将简化模型的设计结果迭代至精确动力学模型中，需要描述航天器在引力辅助行星附近的轨道和飞行时间。而以行星为中心的B 平面参数［4］就能够准确反映航天器相对行星的双曲线轨道的大小和空间取向，并且在打靶修正时B平面参数与修正脉冲有良好的线性关系。文献［5－6］采用B平面参数研究了火星探测的精确轨道设计。本文将脉冲等效模型求得的引力辅助参数化为目标B平面约束，使用微分修正法改进地心逃逸速度，最终得到了精确模型中的引力辅助轨道。

2 引力辅助简化模型下的轨道计算

在用圆锥曲线拼接法近似设计轨道的时候，采用引力辅助等效脉冲模型，即忽略行星影响球半径，且认为引力辅助使航天器获得瞬时速度脉冲。文献［7］在设计木星探测轨道时提出了引力辅助简化模型下轨道计算的有效方法。引力辅助前后，航天器的日心位置与引力辅助行星位置rPl相同。

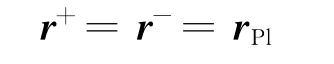
航天器引力辅助时相对于引力辅助行星的轨道为双曲线轨道，双曲线进入剩余速度和离开剩余速度大小相等

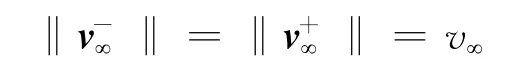
引力辅助对航天器产生的等效脉冲ΔvGA为

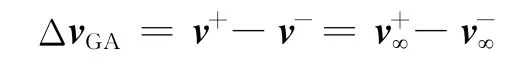
双曲线剩余速度的偏转角为δ根据下式确定

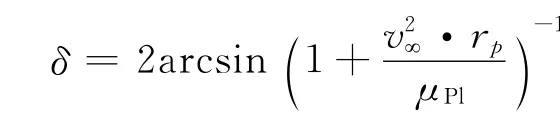
式中 μPl为引力辅助行星引力常数；rp为引力辅助半径。

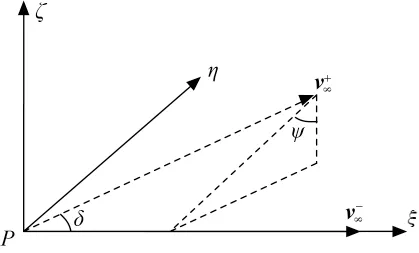
图1 引力辅助坐标系Fig.1 Gravity assist reference frame

为了求得引力辅助给航天器提供的速度增量和引力辅助后航天器的速度，建立行星心引力辅助坐标系P－ξηζ（见图1）。坐标系原点建立在引力辅助行星的中心，ξ轴沿进入双曲线剩余速度方向，ζ轴垂直于由引力辅助前航天器的日心速度v－与引力辅助行星的日心速度vPl所决定的平面，η 轴与ξ、ζ轴构成右手坐标系。三坐标系的单位矢量分别记为i、j和k。

由双曲线轨道的性质可知，离开引力辅助行星的双曲线剩余速度在以进入双曲线剩余速度为轴、顶角为δ的圆锥面上，且大小等于v∞。根据几何关系可以得到

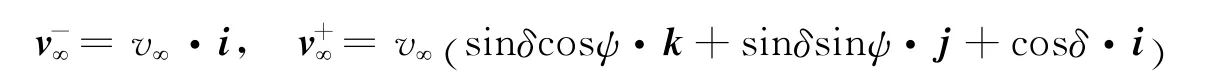
3 精确模型引力辅助轨道设计

3.1 目标B平面参数

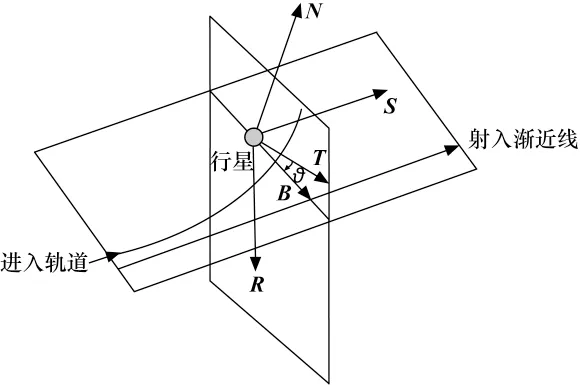
图2 B平面示意［5］Fig.2 B plane

航天器经过行星引力辅助时的双曲线轨道可以通过B平面来描述。B平面参数在进行轨道微分修正的时候具有良好的收敛性。B 平面定义为过引力辅助行星中心并垂直于接近引力辅助行星的双曲线渐近线的平面［4］（见图2）。

S为射入渐近线方向的单位矢量，即

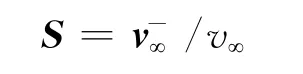
为了方便起见，参考方向单位矢量N 取黄道平面法线方向。T 矢量和R 矢量定义为

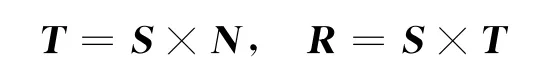
B 矢量由引力辅助行星中心指向B 平面与射入渐近线的交点，其大小等于双曲线轨道的半虚轴。B平面参数BT和BR定义如下：

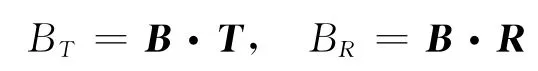
根据引力辅助等效脉冲模型确定的双曲线轨道进入和离开双曲线剩余速度即可计算微分修正时的B平面参数。首先，双曲线轨道平面法向量n为

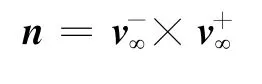
双曲线轨道半长轴为

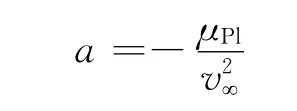
B 矢量的大小等于双曲线轨道的半虚轴大小b

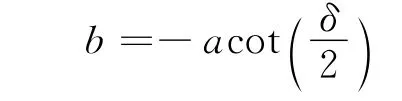
因此，目标B 矢量可以表示为

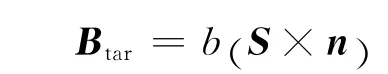
从而可以求得目标约束B平面参数BTtar和BRtar。

3.2 实际B平面参数

微分修正时可以根据进入行星影响球时的位置r、速度v求出实际S 矢量，进而求出实际B平面参数

3.3 时间参数

在精确模型引力辅助轨道设计时，通常将脉冲等效模型搜索得到的引力辅助时间tGA认为是航天器实际飞行到达近行星点的时刻。但是由于模型不同，在精确动力学模型中积分至tGA时刻求得航天器飞行轨道，航天器相对行星的双曲线轨道一般并没有到达近行星点或已经超过近行星点。航天器的当前状态距离近行星点的时间可以根据其位置、速度信息计算，公式为

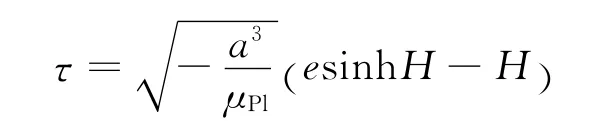
式中 H为双曲角。

3.4 微分修正

建立描述航天器深空飞行的精确动力学模型，考虑太阳引力、各大行星的引力和太阳光压力。引力辅助微分修正的设计变量选为地心逃逸速度vp，约束变量有目标B 平面参数BTtar和BRtar，另外，为了保证脉冲搜索得到的引力辅助时间为近行星点时间，需要设定航天器积分结束时距离近星点时间约束τtar为0。约束变量的响应和设计变量的扰动所满足的函数关系线性化后有

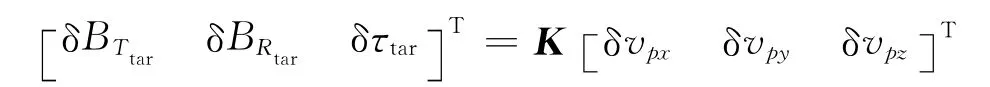
式中 K为约束变量对设计变量的敏度矩阵。由于精确动力学模型较为复杂，敏度矩阵K 通常根据数值方法求得。那么可以得到为了消除末端误差从而需要对设计变量施加的扰动

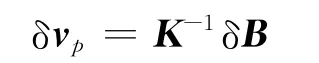
在满足引力辅助约束后，由于存在模型误差，航天器还无法如二体问题设计结果那样飞到目标天体，因此，还需要进行第二次以任务目标星体为约束的轨道修正。若探测目标为小行星，末端约束应为航天器和小行星的日心位置误差；若探测目标为火星等大行星，则末端约束应设定为目标火心轨道倾角、近火点或火星中心B 平面参数。以第一次引力辅助修正结果为初值，可以较快得到满足精度的设计结果。

4 算例及分析

本节以地球出发利用火星甩摆交会8号小行星花神星的轨道为例，说明本文设计方法的有效性。8号花神星是1颗主带小行星，也是与太阳距离最近的较大的主带小行星。花神星的轨道要素如表1所示。

表1 J2000日心黄道坐标系下花神星的轨道要素（MJD 55600）Tab.1 Orbit elements of Flora in J2000heliocentric ecliptic reference frame（MJD 55600）

4.1 等效脉冲模型轨道初步设计

在进行初步轨道设计时，基于日心二体模型，引力辅助采用等效脉冲模型。设计变量选为地球出发时间t0、火星甩摆时间tM、小行星到达时间tf以及火星引力辅助变量rp和ψ，优化搜索算法为粒子群算法（PSO）。火星甩摆时的最低高度设为300km，出发时间选为2020年1月1日（MJD 58849）至2025年12月31日（MJD 61040）。轨道初步设计结果如表2所示。

表2 简化模型引力辅助初步设计结果（J2000日心黄道坐标系）Tab.2 Preliminary design result by the simplified model（J2000heliocentric ecliptic reference frame）

4.2 精确轨道迭代设计

选择地心停泊轨道高度为300km，赤道倾角为22°。计算得到的地心逃逸轨道参数如表3所示。

表3 地心轨道设计结果（J2000地心黄道坐标系）Tab.3 Design result of earth－centred orbit（J2000earth－centred ecliptic reference frame）

以逃逸双曲线近地点速度为设计变量，两次微分修正结果如表4、表5所示。

表4 第一次微分修正结果（J2000火心黄道坐标系）Tab.4 Result of first differential correction（J2000 Mars－centred ecliptic reference frame）

表5 第二次微分修正结果（J2000日心黄道坐标系）Tab.5 Result of second differential correction（J2000 Mars－centred ecliptic reference frame）

精确模型中航天器的日心飞行轨道如图3所示。航天器到达火星引力辅助时相对火星的双曲线轨道如图4所示。

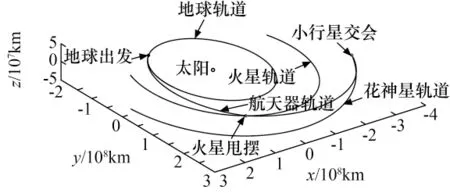
图3 日心轨道（J2000日心黄道系）Fig.3 Sun－centred trajectory（J2000heliocentric ecliptic reference frame）

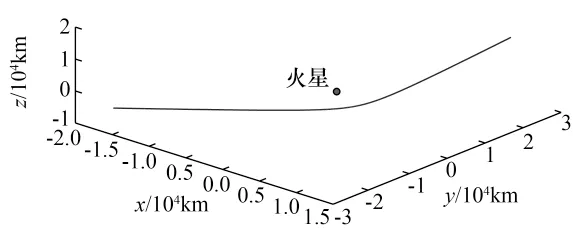
图4 火星甩摆时相对火星的轨道（J2000火心黄道系）Fig.4 Orbit during Mars gravity assist（J2000 Mars－centred ecliptic reference frame）

4.3 结果分析

由表4和表5可以看到，两次微分修正的迭代次数较小，说明本文设计含精确引力辅助轨道方法的高效性。其次，从图3可知本文的设计方法能够使得航天器在精确动力学模型下成功实现引力辅助，并在末端时刻精确到达目标位置。此外，根据轨道设计结果，简化模型脉冲搜索、第一次微分修正和第二次微分修正所得到的设计变量，即地心逃逸近地点速度大小，有所不同，但差别均非常小（见表3～5）。这说明简化等效脉冲模型精度较高，使用其对引力辅助过程进行近似有较高的合理性和可信度。

5 结束语

本文给出了精确动力学模型下，通过微分修正设计含引力辅助轨道的一种有效方法。精确模型相比于传统的简化模型，在动力学方程中引入了摄动，并将引力辅助看作连续的过程，符合工程实际情况。另外，通过算例分析可知，精确模型与简化模型计算参数相差不大，说明使用引力辅助等效脉冲模型的简化模型精度较好，且以简化模型结果为基础，通过微分修正几次迭代即可得到满足目标约束的精确引力辅助模型下的结果。

在本文的基础上，可以进一步研究用B 平面设计多次精确引力辅助探测轨道方法。此外，精确引力辅助模型下航天器小推力轨迹优化也是下一步研究内容。

［1］SIMS J A.Delta－V Gravity－Assist Trajectory Design：Theory and Practice ［D］.Dissertation，School of Aeronautics and Astronautics，Purdue University，MI，1997.

［2］JV BREAKWELL，LM PERKO.Matched asymptotic expansions，patched conics and the computation of interplanetary trajectories［C］.AIAA／AAS Astrodynamics Specialist Conference，AIAA Monterey，CA，1965：685－689.

［3］STEPHEN S BAYLISS.Precision targeting for multiple swing by interplanetary trajectories［D］.Measurement Systems Laboratory，Massachusetts Institute of Technology，Cambridge，Massachusetts，1970.

［4］KIZNER W.A method of describing miss distances for lunar and interplanetary trajectories［J］.Planetary and Space Science，1961（7）：125－131.

［5］陈杨，赵国强，宝音贺西，等.精确动力性模型下的火星探测轨道设计［J］.中国空间科学技术，2011，31（1）：8－15.CHEN YANG，ZHAO GUOQIANG，BAOYIN HEXI，et al.Orbit design for Mars exploration by the accurate dynamic model［J］.Chinese Space Science and Technology，2011，31（1）：8－15.

［6］赵国强，宝音贺西，李俊峰.基于B 平面的火星探测直接转移轨道设计方法 ［J］.中国空间科学技术，2012，32（1）：1－7.ZHAO GUOQIANG，BAOYIN HEXI，LI JUNFENG.Direct transfer trajectory design for Mars Exploration Using B－plane［J］.Chinese Space Science and Technology，2012，32（1）：1－7.

［7］陈杨，宝音贺西，李俊峰.木星探测轨道分析与设计 ［J］.天文学报，2012，53（2）：106－118.CHEN YANG，BAOYIN HEXI，LI JUNFENG.Jupiter exploration mission analysis and trajectory ［J］.ACTA ASTRONOMICA SINICA，2012，53（2）：106－118.