航天器随机振动设计载荷比较

张玉梅 韩增尧 刘绍奎

（北京空间飞行器总体设计部，北京 100094）

1 引言

在全寿命期间，航天器要经历不同类型的动力学环境，其中包括：噪声、随机振动、冲击、低频瞬态振动等［1］。将上述动力学环境载荷等效为准静态的设计载荷，是目前航天器结构强度设计采取的主要方法。对于航天器主结构来说，主要考虑恒加速度环境以及低频（150Hz以下）振动。制定低频振动设计载荷的主要方法有：质量加速度曲线（MAC）、广义模态冲击谱、瞬态分析以及耦合载荷分析［2］。次级结构的强度设计则需要综合考虑和权衡正弦振动环境、噪声环境和随机振动环境。对于同时发生的动力学环境，则需要耦合其设计载荷。耦合方法有直接相加、概率联合分布和蒙特卡罗等方法。

结构在随机振动下的失效形式分为首次穿越失效和疲劳失效两种［3］。将随机振动载荷等效为准静态载荷是基于首次穿越失效模式，不考虑疲劳破坏。在航天领域，从20世纪60年代起就有学者研究如何将随机振动载荷等效为准静态载荷［4］；在地震领域中，该问题也受到很多学者关注。但是，将随机振动载荷等效为准静态载荷的等效原则一直是比较模糊的概念。迄今为止，还没有一个能够被广泛接受的标准规范用于设计和验证振动环境的等效过程。归纳现有的等效方法，可将其等效原则分为三种：加速度峰值响应等效、位移峰值响应等效以及应力峰值响应等效。本文重点比较了加速度峰值响应等效和位移峰值响应等效的设计载荷。

2 两种等效原则简介

（1）基于加速度峰值响应等效的设计载荷

加速度峰值响应等效即设计载荷所产生的加速度响应与随机振动中的加速度响应峰值是相等的。外载荷激励条件下，加速度峰值响应等效的设计载荷计算公式为

式中 Fa为加速度峰值响应等效的设计载荷；M为质量矩阵；F（t）为随机载荷；K为刚度矩阵；C为阻尼矩阵；x为位移向量为速度向量为加速度向量。

由公式（1）可以看出，计算设计载荷的关键步骤是计算加速度峰值响应。常用的加速度峰值的估算方法有Miles公式法、试验规范法、全频段功率谱密度法、模态质量参与法、半功率点法、加权的半功率点法和有限频段法。上述几种方法都是假设加速度响应呈零均值高斯分布，然后根据3σ准则得到其加速度峰值。目前，我国航天领域常用的是全频段的功率谱法，其公式为［5］

式中 S为加速度响应谱密度。一般来讲，有限元分析法适用于低频段，高频段采用统计能量法。但是在实际工程计算中，有限单元法应用较为普遍。

2001年，Chung Y T 提出了有限频段法，公式为［6］

式中 f0为积分频率上限。

有限频段法是根据波音公司和NASA 的试验结果，发现结构高频部分的应变收敛很快，而加速度收敛很慢，因此，应该以应变的收敛区间确定加速度积分的范围。根据波音公司的测量结果，结构响应的应变通常在300～400Hz收敛［7］，建议计算随机振动响应峰值的积分区间应取为20～300Hz。文献［8］总结了国内噪声试验的结果，发现次级结构在600Hz附近应变收敛。由此看出，不同的结构形式在不同种类的随机激励下，其积分上限存在一定的差异，目前仍没有一个统一的认识。

有限频段法的重要意义在于对加速度峰值响应等效原则提出了质疑，即对结构进行强度设计时关注的参数应该是应变而非加速度。文献［9］回顾了美国航天40年发展，并提出载荷设计关心的参数不应该是加速度而应该是应变或者力。

（2）基于位移峰值响应等效的设计载荷

随机振动的设计载荷问题在土木工程行业也很受重视。文献［10］提出以位移峰值响应等效来制定等效静态载荷，并给出了等效静态载荷的具体定义：当结构承受动态载荷时，在某一时刻，结构都发生变形从而形成一个位移场。如果一个静态载荷，能够产生相同的位移场，则称该静态载荷为这一动态载荷在某一时刻的等效静态载荷。

外载荷激励下，设计载荷计算公式为

式中 Fx为基于位移响应等效的设计载荷，其余参数与式（1）相同。由于刚度矩阵是系统固有参数，因此该方法中最重要的是计算位移峰值。传统的随机振动响应分析方法均可用于获得结构的位移响应，航天工程中最为常用的手段是利用一些商业软件，如NASTRAN 等，进行随机振动有限元分析。通过数值分析可以得到位移均方根值，假设位移响应亦呈零均值高斯分布，那么根据3σ准则可以得到其峰值位移：

式中 S1为位移响应谱密度。

3 基于解析法的设计载荷对比

3.1 基于单自由度振动模型的设计载荷比较

图1 基础激励下的单自由度振动模型Fig.1 Single－degree－of－freedom vibration model with moving base

基础激励下的单自由度振动模型如图1所示。

假设激励为白噪声，则根据线性随机振动理论，可以得到相对位移的方差响应为［11］

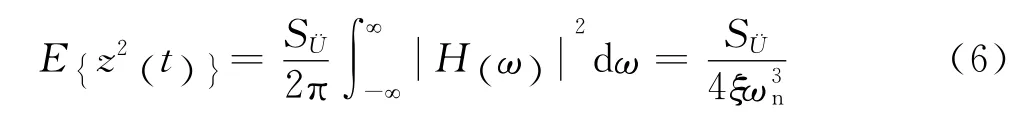
式中 ωn＝2πfn，fn为固有频率；2S¨U为白噪声常数；ξ为系统阻尼比；z（t）＝ x（t）－u（t），z（t）为相对位移，x（t）为绝对位移，u（t）为基础位移

亦可以得到绝对加速度的均方响应为

由位移峰值等效得到的设计载荷为

式中 k为系统刚度。

由加速度峰值响应等效得到的设计载荷为

式中 m为系统质量。

两种设计载荷相比可得

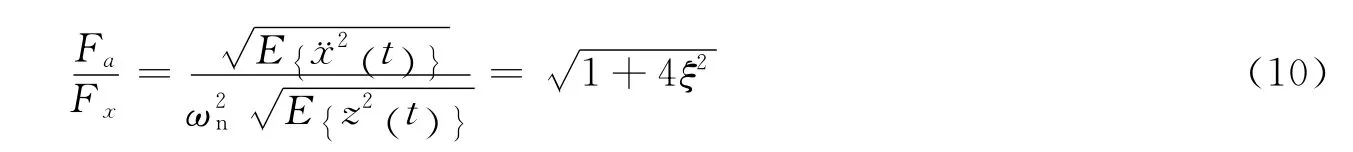
通常ξ数值比较小，由此看出加速度峰值响应等效的设计载荷与位移峰值响应等效的设计载荷基本相等。

3.2 基于二自由度振动模型的设计载荷比较

图2是二自由度振动模型示意，其系统的运动微分方程为［12］

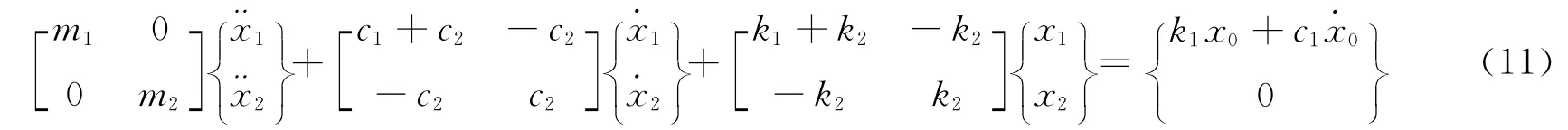
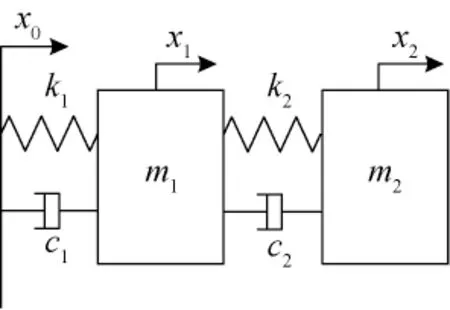
图2 二自由度振动模型Fig.2 Two－degree－of－freedom vibration model

假设：

绝对加速度的均方响应为

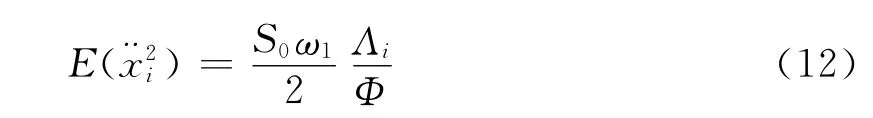
式中 i＝1，2；S0为白噪声常数。

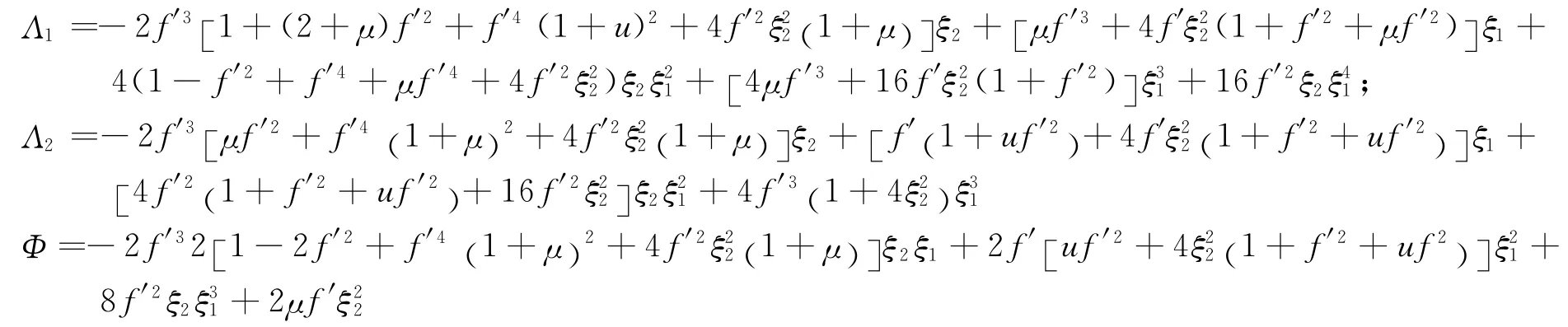
相对位移响应的表达式为

式中 i＝1，2；质量m2相对位移响应Δ2表达式为

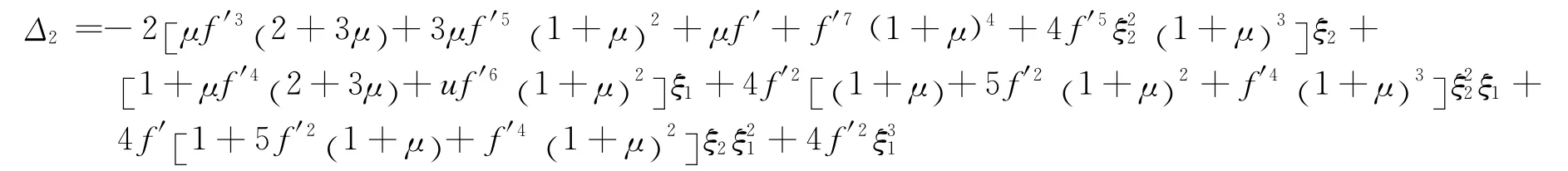
两种设计载荷比为

式中 a1为质量m1的绝对加速度；a2为质量m2的绝对加速度；z2为质量m2相对于基础的位移。

为比较两种设计载荷的大小，假设阻尼比均为0.03，质量（m1）－弹簧（k1）系统的频率为50Hz，质量（m2）－弹簧（k2）系统的频率为100Hz，则设计载荷比与质量比的关系如图3所示。假设阻尼比均为0.03，质量m2＝0.01m1，则载荷比值与频率比f′的关系如图4所示。

由分析可知，设计载荷比随着频率比以及质量比的增大呈单调递减，并最终趋近于1。因此可见，在假设阻尼比均为0.03的情况下，二自由度振动模型中，基于加速度的设计载荷要不小于基于位移的设计载荷。

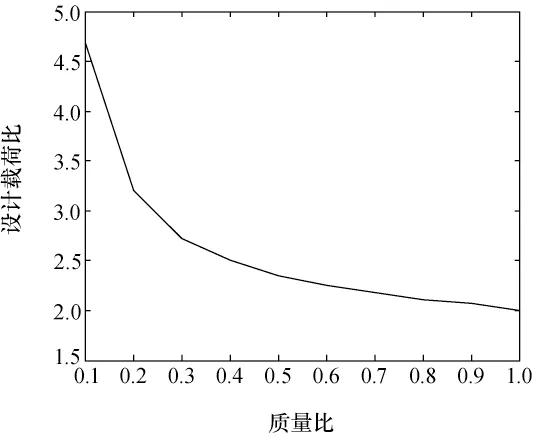
图3 载荷比与质量比的关系Fig.3 Relationship between the ratio of two loads and the ratio of two masses

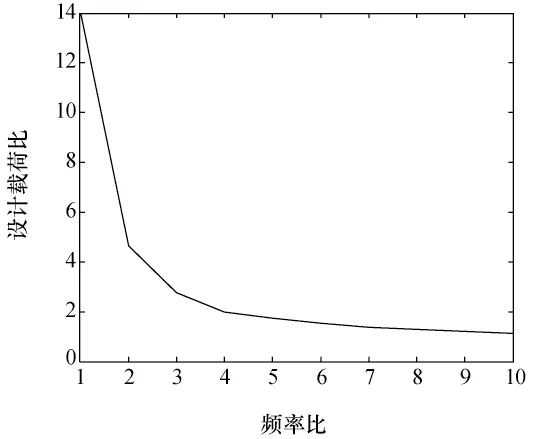
图4 载荷比与频率比的关系Fig.4 Relationship between the ratio of two loads and the ratio of two frequencies

3.3 工程算例仿真分析

为了进一步比较两种设计载荷的关系，以某航天器产品单元为例进行有限元仿真分析。模型如图5所示，为长方盒结构，中空，内有两层隔板，隔板上的安装器件用质量点代替。主体结构为壳单元，底座为实体单元，材料为铝合金。约束方式为4个安装底座全约束，载荷为基础激励。

分析步骤如下：

1）通过随机振动分析，得出隔板上一质量点（节点9048）的加速度响应与位移响应；

2）分别计算出加速度峰值响应与相对位移峰值响应；

3）将加速峰值响应算出设计载荷作为静载荷施加在质量点上，进行静力分析，计算出9048节点位移；

4）与随机振动分析的相对位移峰值进行比较。

载荷条件［13］如表1所示，有限元模型如图5，加速度响应如图6，位移响应如图7所示。

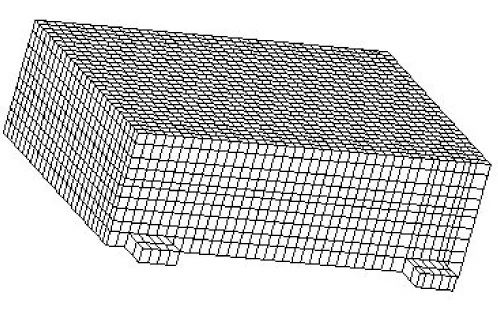
图5 某航天产品有限元分析模型Fig.5 FEM model of a spacecraft apparatus

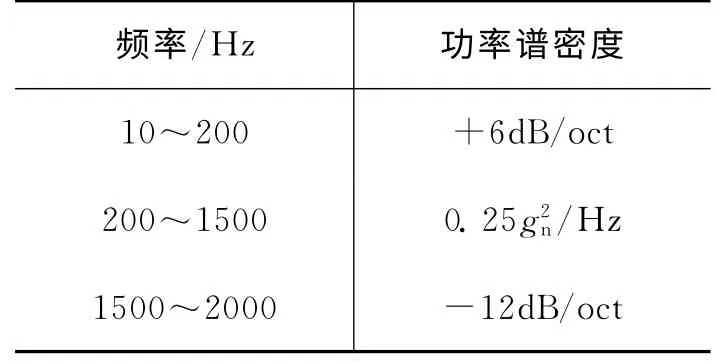
表1 随机振动载荷条件Tab.1 Random vibration test level

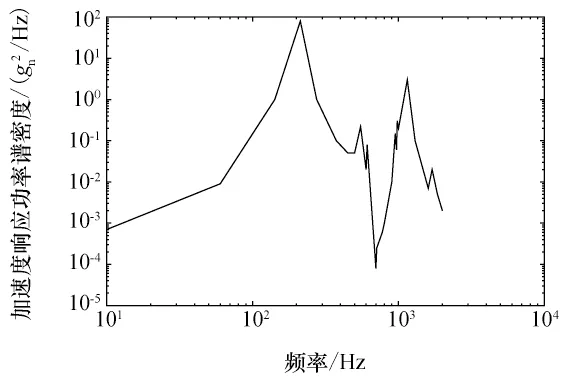
图6 加速度响应功率谱密度Fig.6 Acceleration response PSD

图7 位移响应功率谱密度Fig.7 Displacement response PSD

Z 向加速度3σ峰值响应为76.02gn，9 048质量点为电子元器件，质量为0.007kg，因此设计载荷为5.215N。将设计载荷施加在质量点上，进行静力计算，该点的位移为7.66×10－5m。而随机振动时该点的绝对位移均方响应为3.8×10－5m，底座的位移响应为1.963×10－5m，因此相对位移峰值响应为5.511×10－5m。根据加速度3σ响应等效得到的设计载荷产生的位移比随机振动的峰值相对位移大了约40%。

4 结束语

综合分析可以得出，若试验件为单自由度，在基础激励下，两种等效原则的设计载荷近似相等；若试验件为二自由度模型，加速度峰值等效得到的设计载荷要大于位移峰值等效得到的设计载荷。等效原则的选用取决于破坏机理。在交变载荷下，材料仍然服从弹性力学原理。因此，本文推荐使用基于位移响应等效的设计载荷，该方法将有效减少航天器结构质量。

进一步研究工作包括：

1）开展试验验证。等效原则的改变意味着设计准则的变换，本文只进行了分析计算与仿真，还需要进行充分的试验验证。

2）应力响应等效与加速度响应等效的比较研究。

3）应力峰值的计算方法研究。

［1］向树红.航天器力学环境试验技术 ［M］.北京：中国科学技术出版社，2010：50－52.XIANG SHUHONG.The test technology of spacecraft mechanics environments［M］.Beijing：China Science and Technology Press，2010：50－52.

［2］HARRY HIMELBLAU，DENNIS L KEM，JEROME E MANNING，et al.HDBK－7005Dynamic Environmental Criteria［S］.NASA，Washington D C，2001：21－32.

［3］刘旭华.结构动力可靠性研究 ［D］.哈尔滨：哈尔滨工程大学，2006.LIU XUHUA.Research in structures dynamic reliability ［D］.Harbin：Solid Mechanics department of Engineering University，2006.

［4］MILES J W.On structural fatigue under random loading［J］.Aerospace Sciences，1954，21（11）：753－762.

［5］杨宝宁.随机振动条件下设计载荷的确定方法 ［J］.航天器工程，2006，15（3）：33－37.YANG BAONING.Engineering methods for determining quasi－static limit load for structures under random vibration ［J］.Spacecraft Engineering，2006，15（3）：33－37.

［6］CHUNG Y T，KREBS D J，PEEBLES J H.Estimation of Payload Random Vibration Loads for Proper Structure Design ［C］.Proceedings of 42th Structures，Structural Dynamics，and Materials Conference and Exhibit，Washington D C，AIAA，2001：1667－1675.

［7］LEUNG K，FOIST B L.Prediction of acoustically induced random vibration loads for shuttle payloads［C］.Proceedings of 36th Structures，Structural Dynamics，and Materials Conference and Exhibit，Washington D C，AIAA，1995：1200－1208.

［8］邹元杰.基础激励和声激励下的设计载荷估算方法 ［C］.结构动力学会议，北京：中国振动工程学会，2009：93－101.ZOU YUANJIE.Estimation of design loads under noise or with moving base［C］.Structural Dynamics Conference，Beijing：China Vibration Engineering Academy，2009：93－101.

［9］WADA.Historical overview of structural modeling，design loads and testing of spacecraft［C］.Proceedings 41th of Structures，Structral Dynamics，and Materials Conference and Exhibit，Washington D C，AIAA，2000：1773－1780.

［10］KANG B S，CHOI W S，PARK G J.Structural optimization under equivalent static loads transformed from dynamic loads based on displacement［R］.Proceedings of 40th Structures，Structral Dynamics，and Materials Conference and Exhibit，Washington D C，AIAA，1999：1259－1263.

［11］JAAP WIJKER.Random vibrations in spacecraft structures design ［M］.New York：Dordrecht Heidelberg London，2009，47.

［12］涂永明.CFRP索悬挂建筑结构静力和动力分析及研究 ［D］.南京：东南大学，2005.TU YONGMING.Study on the static and dynamic mechanisms of CFRP cable suspended building structures［D］.Nanjing：Southeast University，2005.

［13］COLEMAN J J.Reliability of Aircraft Structures in Resisting Chance Failure［J］.Operations Research，1959，5（2）：39－44.