巧寻突破点解决复合场问题
戴 伟
(江苏省口岸中学,江苏 泰州 225321)
复合场的问题是高中阶段较难处理的问题,也是各省高考的重点问题,下面列举江苏省2012年压轴题谈谈自己对复合场问题的看法.
原题.如图1所示,待测区域中存在匀强电场和匀强磁场,根据带电粒子射入时的受力情况可推测其电场和磁场.图中装置由加速器和平移器组成,平移器由两对水平放置、相距为l的相同平行金属板构成,极板长度为l、间距为d,两对极板间偏转电压大小相等、电场方向相反.质量为m、电荷量为+q的粒子经加速电压U0加速后,水平射入偏转电压为U1的平移器,最终从A点水平射入待测区域.不考虑粒子受到的重力.
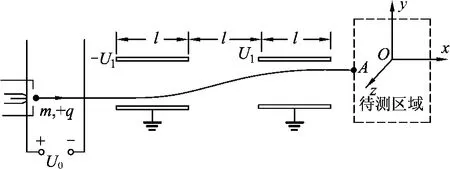
图1
(1)求粒子射出平移器时的速度大小v1;
(2)当加速电压变为4U0时,欲使粒子仍从A点射入待测区域,求此时的偏转电压U;
(3)已知粒子以不同速度水平向右射入待测区域,刚进入时的受力大小均为F.现取水平向右为x轴正方向,建立如图所示的直角坐标系Oxyz.保持加速电压为U0不变,移动装置使粒子沿不同的坐标轴方向射入待测区域,粒子刚射入时的受力大小如表1所示.
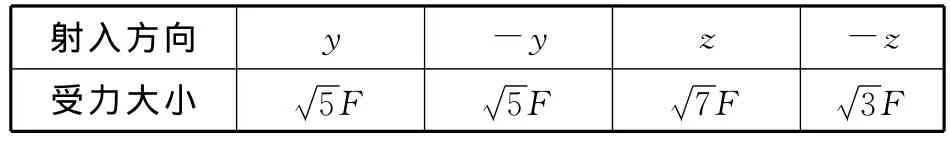
表1
请推测该区域中电场强度和磁感应强度的大小及可能的方向.
这道题的第1、2个问题难度较低,第3个问题是一道较复杂的电磁与磁场的混合场问题.
第1、2两问题的解答过程如下:
(1)设粒子射出加速器的速度为v0,由动能定理有.由题意得v1=v0,即
(2)在第1个偏转电场中,设粒子的运动时间为t,加速度的大小为,在离开时,竖直分速度为v=at.y竖直位移为,水平位移为l=v1t.
粒子在两偏转电场间做匀速直线运动,经历时间也为t,竖直位移为y2=v2t.
(注:第1,2问的解答为原题标准答案)
在第3个问题中,粒子以不同的方向射入复合场区这种三维方向问题,对个人的空间思维能力和物理思维能力有较高的要求.在解题过程中,要紧紧抓住题目的重要因素,找出突破点,同时,要结合分析不同情况的三维受力、场图,对解题也有较好的帮助.
突破点1:本题的出发点和突破口在“粒子以不同速度水平向右射入待测区域,刚进入时的受力大小均为F”这句话.
速度沿水平方向,如果磁场有竖直方向的分量,速度大小不同时,肯定会受到大小和方向变化的洛伦兹力,因此可以分析出,磁场方向平行于x轴,竖直方向没有磁感应强度B,B的方向平行于x轴(图2、图3).既然无论如何入射,合力大小总为F,可见,没有洛伦兹力时,且忽略重力的情况下,只有电场力为F,电场力的大小与场强E的方向无关,因此电场强度E的方向暂时无法确定.
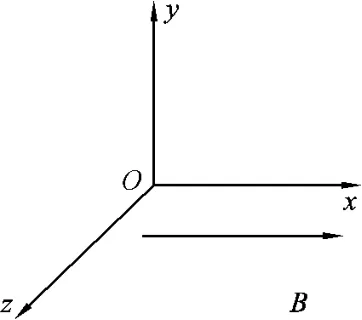
图2
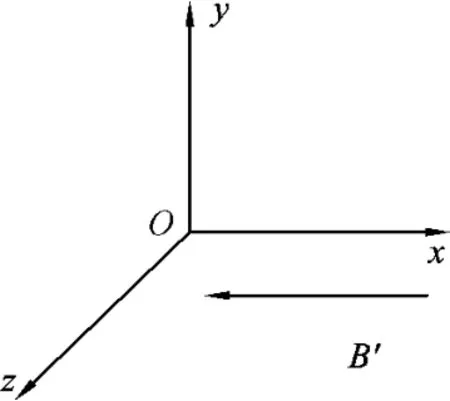
图3
解题过程如下:
突破点2:第2个突破口在粒子沿y轴方向入射的情况.沿y轴方向入射,粒子受到的力为.
粒子y轴入射,由于B平行于x轴,洛伦兹力的大小不会变化,而且电场力仍为F,可以判定洛伦兹力f与电场力F垂直(图4),如果不垂直,当粒子的入射方向相反时,合力的大小将会发生变化(图5).B是平行于x轴方向的,根据左手定则可判定,洛伦兹力方向必平行于z轴.再可以得出电场力F方向平行于xOy平面,即场强E平行于xOy平面(图6、图7).
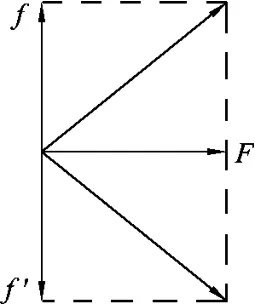
图4
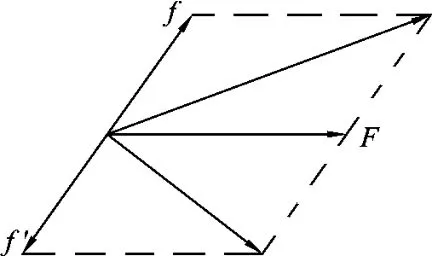
图5
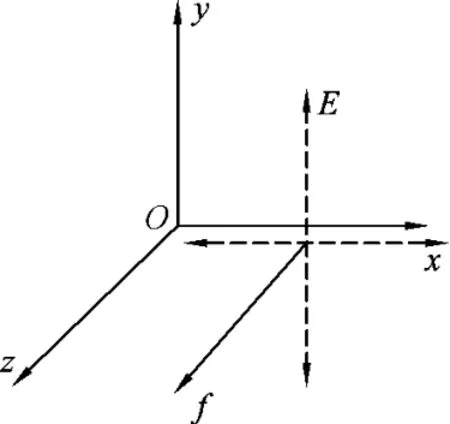
图6
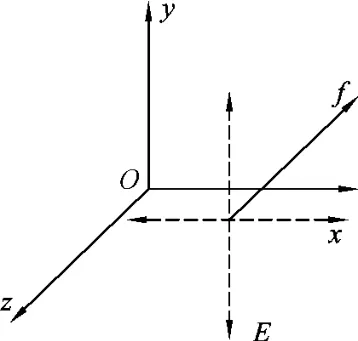
图7
解题过程如下:
由粒子沿±y轴方向射入时的受力情况可知:E与Oxy平面平行,有F2+f2=,则f=2F,且f=B,解得
突破点3:粒子在竖直方向的受力情况以及联系前面的两个突破口,磁感应强度方向平行于x轴,电场强度E的方向平行于xOy平面.
当粒子沿z轴方向入射时,速度方向与磁感应强度B方向垂直,洛伦兹力沿y轴方向(见图8、图9),共4种情况.
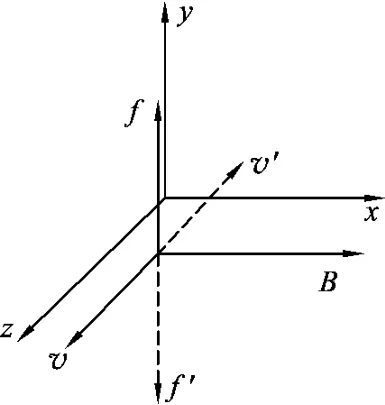
图8
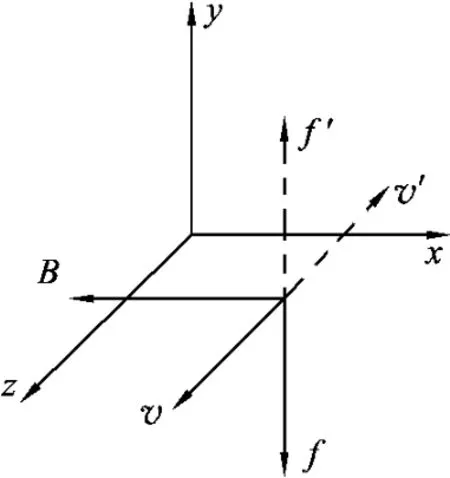
图9
电场方向与x轴方向有一定的夹角,假设夹角为α,电场力在xOy平面内,与洛伦兹力f不垂直.因此要对电场力F进行分解.
解题过程如下:
(1)若B沿+x轴方向,当粒子沿z轴正方向射入时,洛伦兹力方向沿y轴正向(图8实线).如果电场力F有沿y轴正向的分力(图10).
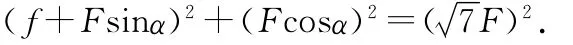
当粒子沿z轴负方向时,洛伦兹力沿y轴负方向(图8虚线、图10).
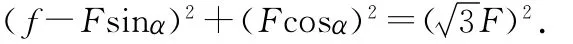
解得α=30°,或α=150°.
即E与Oxy平面平行且与x轴方向的夹角为30°或150°.
如果电场力F有沿y轴反向的分力.可以解得α=-30°或α=-150°.
即E与Oxy平面平行且与x轴方向的夹角为-30°或-150°.
(2)若B沿-x轴方向时,当粒子沿z轴正方向射入时,洛伦兹力情况(图9实线).
当粒子沿z轴负方向时,洛伦兹力情况(图9虚线、图11).
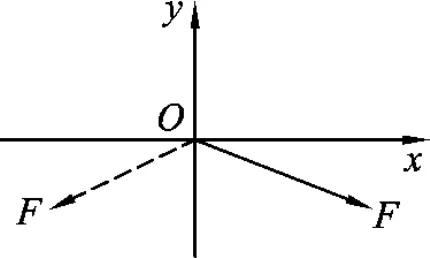
图11
同理可解得α=±30°,或α=±150°.
所以E与Oxy平面平行且与x轴方向的夹角为±30°或±150°.
通过这道题目分析可以发现,解决复合场的问题时,要善于抓住题目的突破口,从突破口出发,结合电场力、洛伦兹力的性质进行分析,同时考虑各种情况,就能较好解决问题.

