对我国两种海堤规范设计波浪标准的风险分析

刘德辅，史宏达，王风清

(1.中国海洋大学 防灾研究所，山东 青岛 266003;2.中国海洋大学 工程学院，山东 青岛 266100)

随着全球气候变暖、海平面上升等因素加剧的趋势，台风，巨浪，暴潮，暴雨巨灾已成为影响太平洋沿岸及亚洲各国人民生命财产安全和经济发展的重大问题。就中国而言，巨灾已直接影响到沿海和内陆十多个省份数以亿计人口的生命财产和经济可持续发展。2006年桑美和碧利斯两场台风，共导致1 600 多人死亡和失踪，5 000 多亿经济损失。桑美台风诱发了7 m 巨浪和3.8 m 风暴增水，导致沙埕港952 只船舶沉没，1 594只船舶毁坏。如果台风延后两小时登陆，则恰逢天文大潮，这种“三碰头”的组合，可完全淹没包括若干个核电站在内的福建、浙江大部分土地。其灾难性后果难以估量。这种小概率极端事件的发生是完全可能的。亚洲其他国家所遭受的台风—暴雨，暴潮灾害同样触目惊心:1959年日本伊势湾遭受台风(Vera)暴潮袭击，造成5 180 人死亡，受灾人口达150 万。1970年11月印度洋上的热带风暴波罗，风暴潮高达6 m，造成孟加拉国30 万人死亡，100 多万人无家可归。1991年4月热带风暴哥奇造成14.3 万人死亡。2008年热带风暴Nargis 造成缅甸10 万人死亡。

长期以来，由于概率统计理论和方法上的限制，在港口、海岸、近海及河口城市防护工程的设计中，考虑恶劣环境条件下多种荷载共同作用组合的问题尚未得到妥善解决。多数情况下，仍停留在对实测资料多年最大值概率分析基础上，假定年最大值服从某种分布(Gumbel，Weibull 或P-Ⅲ型分布等)，估计不同重现期对应的设计波高，水位，风速作为设计标准。由于每年只取一个样本，忽略了概率论的一个基本定理——大数定理，造成大量有效信息无法被利用，影响到概率预测的正确性和设防标准的合理性，导致极端气候因素诱发的溃坝，决堤巨灾时有发生。这里对水利部海堤工程设计规范(SL435-2008)推荐的Gumbel 分布及交通部国家行业标准《海港水文规范》(JTJ213-98 2008 修订版)推荐的复合极值分布(CEVD)作为设计波高概率预测设计标准进行风险评估，并介绍复合极值分布在国内外的应用，以期工程设计达到防灾减灾的目的。

1 一个台风致灾因素概率预测新理论—复合极值分布理论的建立

自20 世纪70年代初交通部“海港水文规范编写组”成立以来，进行了全国各地港口的调查研究，特别是1972年3 号台风重创大连港，有效波高6.8 m，超过了1896年台风波高，导致大连港空前损失;1973年召开的“1972年3 号台风研讨会”，更进一步加深了对台风波浪长期概率预测重要性的认识，有关单位开展了针对台风特征进行台风影响海区各种致灾因素(风速、增水、波浪等)概率预测理论和计算方法的研究。

考虑到台风影响不同海区每年出现的频次各不相同，可用离散型随机变量及相应的离散型概率分布表示;而台风诱发的致灾因素(风速、增水、波高等)，则可用连续型极值分布表示。二者的组合经过严格的数学推导，可构成一种新的极值分布模式—复合极值分布(compound extreme value distribution，简称CEVD)［1-2］。考虑到国内外惯用年极值系列按照某种概率模式(如P-Ⅲ型、Gumbel，Weibull 分布)外延推求不同重现期设计值的作法存在的弊端——遗漏了每年各次台风波浪提供的重要信息，影响到概率预测结果的置信度;CEVD 模式引入了台风每年影响不同海区的频次，作为一组离散型随机变量，将每次台风过程波浪的最大值作为连续型随机变量，将一个离散型分布和连续型极值分布组合起来，以顺序统计学和测度论作为推导的理论依据，推导出了CEVD 模式。根据统计检验结果，台风(飓风)影响各海区的频次符合Poisson分布，台风(飓风)波浪的不同特征，可采用Gumbel 和Weibull 分布，则可构成Poisson-Gumbel CEVD 分布(用于我国台风影响海域)［2］和Poisson-Weibull CEVD 分布(用于美国墨西哥湾和大西洋沿岸)［3］。

Poisson-Gumbel 复合极值分布(CEVD):

当台风频次为泊松分布，波高符合Gumbel 分布时，可简化为

式中:α=σn/S;u=ˉH－yn/α;ˉH，S 分别为各次台风波高的平均值和均方差;σn，yn可由表1 根据波浪总个数n 查得。

表1 yn、σn 与波浪总个数n 关系Tab. 1 Parameters yn and σn for different wave data n

计算置信区间的计算公式如下［4］

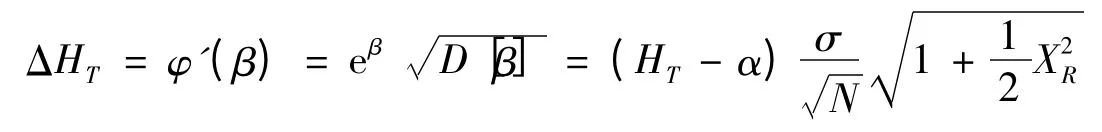
置信区间(置信概率68.27%)为［HT+ΔHT，HT－ΔHT］。

2 P-Gumbel，Gumbel 和P-Ⅲ三种设计波高概率预测模式实例计算及误差评估

2.1 台风过程取样与传统的年极值取样的比较

用台风过程取样代替传统的年极值取样是复合极值分布的最大优点，可使用多于年极值取样λ 倍的资料信息，减低了概率预测结果的误差，从而提高了概率预测结果的可靠性和合理性。表2 显示我国沿海台风影响频次平均高于年极值取样的4 至6 倍，以香港为例，年极值取样47 个样本资料，而CEVD 台风过程取样则可使用291 个样本资料信息。

表2 我国东南沿海台风影响频次统计表Tab.2 Typhoon occurrence frequency in China's south-east coasts

说明:国家行业规范“海港水文规范”专题“台风影响海区设计波浪概率预测理论和计算方法”经谢世楞院士等专家组审查，批准正式纳入2008年“海港水文规范”修订稿条文。由于交通部海港、河港合一新规范的编制，拖延至今，即将出版。

2.2 使用滑动20年取样资料样本对三种模式拟合误差检验

将中科院南海所提供的1951 ～2002 实测(缺测部分为后报)近岸风、浪资料，分别按各20年为一组进行滑动取样，对Gumbel，P-Ⅲ和CEVD 分布的拟合优度，按拟合最大偏差Dn ，拟合平均差v 和拟合标准差d 进行比较，如图1 及表3 所示(有关统计特征及拟合优度说明，详见文献［5］)。

如表3 计算结果和图1 所示，无论是拟合最大偏差Dn，还是拟合平均差v 和拟合标准差d，复合极值分布的拟合偏差数均小于P-III 分布和Gumbel 分布。

2.3 P-Ⅲ，Gumbel 及CEVD 三种模式预测结果对比

以大鹏湾、黄海某岛(黄海某岛为海军有关部门提供资料)及三亚的样本资料为基础，用P-Ⅲ，Gumbel和CEVD 三种模式进行预测，其计算结果及相对误差见表4、5 和图2。

图1 三种分布的拟合Dn，v 和d 对比图Fig.1 Comparison of maximum deviation Dn，v and d of 3 models

表3 三种分布拟合优度参数及其变化范围Tab.3 Comparison between confidence intervals of Dn，v of 3 models

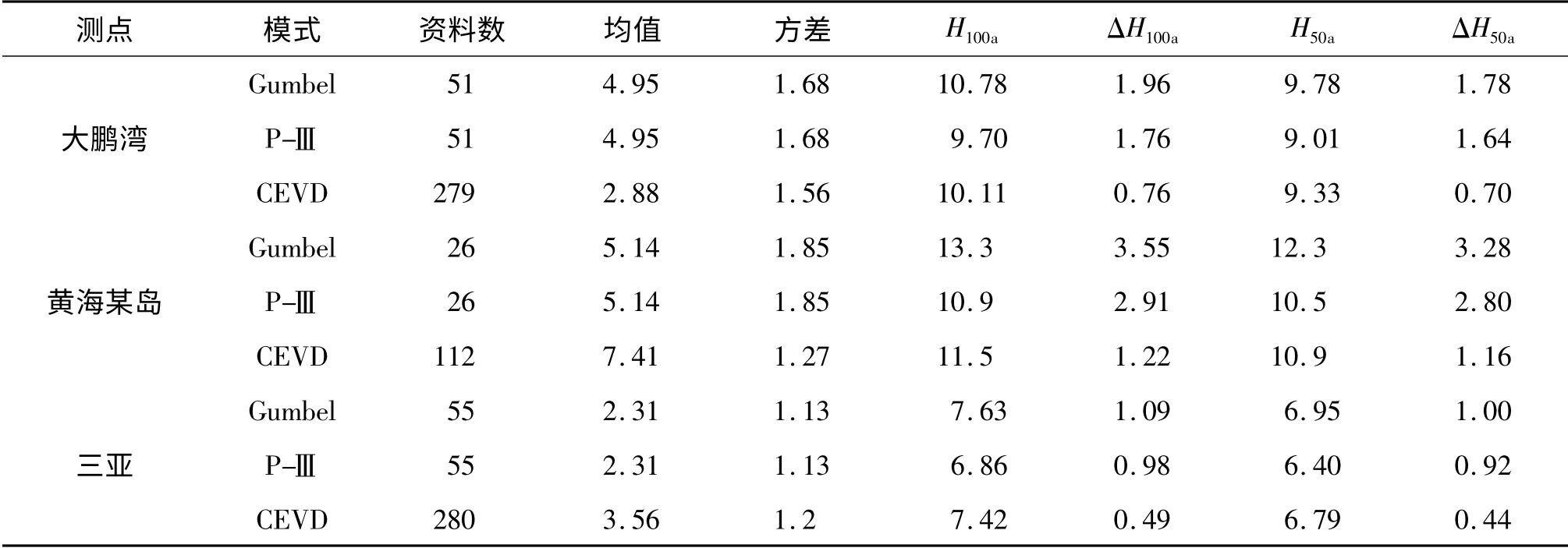
表4 几个地点三种模式下预测计算结果Tab.4 Comparison between predicted design wave heights of 3 models with confidence intervals for Daponwa coast in South China Sea

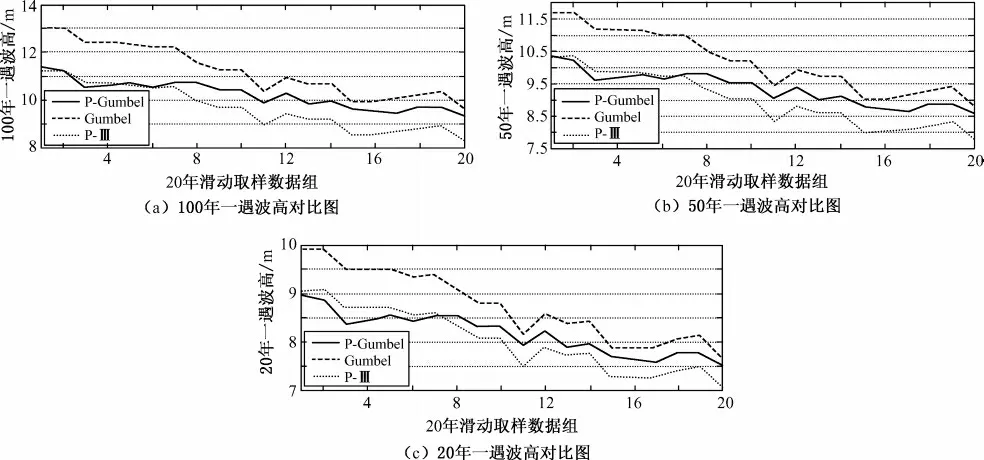
图2 三种分布不同重现期波高对比Fig.2 Wave heights of different return periods predicted by 3 models

表5 三种分布预测值的相对误差Tab.5 Relative error of predicted return value by 3 models

对比计算结果表明，复合极值分布的预测值介于P-III 分布和Gumbel 分布之间，这一结论与Langley R M A H El-Shaarawi［6］得出的结论是一致的。事实证明，水利规范四十年一直建议的P-III 型模式和2008年建议的Gumbel 模式，都是年极值取样，其预测结果置信区间高于复合极值模式两倍。

3 复合极值分布理论在实际飓风灾害预测中的验证

复合极值分布于1982年用于美国沿岸概率预测［3］。正是由于NOAA 规范的错误，导致2005年卡特里娜飓风巨灾，证明了复合极值分布的1982年预测结果的正确性(表6)，使得复合分布在国内外大量引用和应用。2006年我们首次在灾后重大国际会议上指出:按照NOAA 提出的SPH(标准设计飓风)和PMH(可能最大飓风)作为设计标准和校核标准的错误［7］，是这场灾难的根本原因。两场飓风的强度和特征，不仅验证了使用复合极值分布理论1982年预测结果的正确性，同时也显示了2005 灾后使用多维复合极值分布(MCEVD)应用于卡特里娜飓风及其诱发的灾害海况联合概率分析的合理性［8-12］。如果使用CEVD 或MCEVD 预测的100年一遇和1 000年一遇致灾因素作为设计标准和校核标准，Katrina 巨灾是可以预防的［13-14］(见表6)。

表6 墨西哥湾A 区卡特里娜飓风强度概率分析Tab.6 Probability analysis of hurricane Katrina along Gulf of Mexico coasts

飓风的强度和特征，验证了使用复合极值分布理论1982年预测结果的正确性。使用2002年以来新开发的多维复合极值分布理论模式——泊松–嵌套三维逻辑复合极值分布(poisson-nested logistic trivariate compound extreme value distribution，PNLTCED)分析飓风及其诱发的灾害海况如图3 所示，按照NOAA 对墨西哥湾和大西洋沿岸划分为十一个海区后，美国学者Georgion［15］，Casson［16］和Coles［17］对上述海域极端风速预测成果，明显低于PNLTCED 的预测值(文献［11］中图6)。PNLTCED 的预测结果显示，重现期100年一遇的风速3 区(新奥尔良区)与2005 卡特里娜飓风状况相近，明显高于设防标准;8-9 区(新泽西，纽约沿岸)则与2012年桑迪飓风最大风速相近。

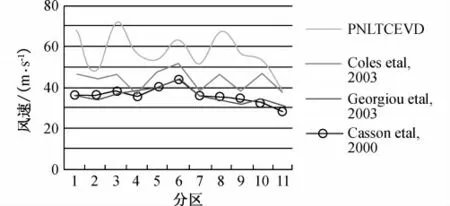
图3 100年一遇的极端风速概率预测Fig.3 Comparison of 100-yr.hurricane wind speeds by using different methods

同样，1982年预测的风暴增水(文献［3］中的图8)，费城(图中虚线)的100年一遇风暴增水达到3 m，完全被2012年桑迪飓风造成新泽西、纽约、特拉华州大面积淹没的事实所证实(见图4)。

迄今为止，该理论在国内已有45 项工程中应用于设计波高概率预测，并在美国、加拿大、韩国、毛里塔尼亚、地中海、挪威等多项工程中引用和应用［6，18-22］。2008年美国在防护飓风灾害工程研究中［22］，引用了四篇论文［2-3，8-9］作为防护飓风灾害设防标准的依据。国家防汛抗旱总指挥部办公室委托完成的“中国沿海台风灾害区划、防台风标准应急制定、防台风应急评估标准制定”正式用于防灾工作实践［23］。

图4 美国大西洋沿岸不同重现期风暴增水Fig.4 Long term distribution of hurricane storm surge

4 结 语

对比两种规范条文中分别建议采用Gumbel 分布和复合极值分布用于设计波高概率预测，前者基于年极值取样，复合极值分布以过程取样代替传统的年极值取样，可使用更多的资料信息，有严格的理论推导为依据，减低了概率预测结果的误差，从而提高了概率预测结果的可靠性和合理性。重大海岸工程设防标准的确定，绝非简单的学术问题。卡特里娜和桑迪飓风灾害的教训，必须引以为戒。

致谢:对邱大洪院士、谢世楞院士及中交一航院、三航院、四航院、海军设计总局、中科院南海所有关专家二十多年来对本理论研究提供的建议、资料和工程应用，深表谢意。

［1］刘德辅，马逢时.极值分布理论在计算波高多年分布中的应用［J］.应用数学学报，1976(1):23-37.

［2］Liu T F，Ma F S.Prediction of extreme wave heights and wind velocities［J］.Journal of the Waterway Port Coastal and Ocean Engineering，ASCE，1980，106(4):469-479.

［3］Liu T F.Long term distribution of hurricane characteristics［C］//Offshore Technology Conference，Houston，USA，Proceedings of OTC 4325.1982:305-313.

［4］Liu D F，Kong L S，Zuo J C，et al.Stochastic-numerical model of tidal current field for Jiaozhou bay of Yellow sea［C］//Proc.ISOPE.2001，3:682-685.

［5］Ochi M K.Applied Probability and Stochastic Processes in Engineering and Physical Sciences［M］.A wiley-interscience publication，JOHN WILEY ＆ SONS，US.1990.

［6］Langley R M，El-Shaarawi A H.On the calculation of extreme wave heights:A review［J］.Ocean Eng，1986，13(1):93-118.

［7］Schwerdt R W，Ho F P，Watking R R.Meteorological Criteria for Standard Project Hurricane and Probable Maximum Hurricane Wind Fields，Gulf and East Coast of the United States［R］.NOAA Technical Report NWS 23，1979.

［8］Liu D F，Pang L，Shi H D.Joint probability analysis of hurricane katrina 2005［C］//Proc.Intern.Offshore ＆ Polar Eng.Conference(ISOPE2006).2006:74-80.

［9］Liu D F，Pang L，Xie B T.Typhoon disaster zoning and prevention criteria-a double layer nested multi-objective probability model and its application［J］.Science in China(E)，2008，51(7):1038-1048.

［10］Liu D F，Shi H D，Pang L.Disaster prevention design criteria for the estuarine cities:new orleans and shanghai-the lesson from hurricane katrina［J］.Acta Oceanologica Sinica，2006，25(4):124-130.

［11］Liu D F，Pang L，Xie B T.Typhoon disaster in China-prediction，prevention and mitigation［J］.Natural Hazards，2009，49:421-436.

［12］刘德辅，庞 亮，史宏达.卡特里娜飓风的启示——有关海岸和水利工程的风险分析［J］.中国工程科学，2007，9(10):24-29.

［13］Bea R.Reliability assessment ＆ management lessons from hurricane Katrina［C］//Proc.Offsh.Mech.＆ Arc.Eng.San Diego.2007:OMAE2007-29650.

［14］GAO.Lake Pontchartrain and Vicinity Hurricane Protection project［R］.GAO-05-1050T，Washington D C，2005.

［15］Georgiou P N，Davenport A G，Vickery P J.Design wind speeds in regions dominated by tropical cyclones［J］.J Wind Eng Ind Aer，1983，13:139-152.

［16］Edward Casson，Stuart Coles.Simulation and extremal analysis of hurricane events［J］.Appl Statist，2000，49(2):227-245.

［17］Stuart Coles，Emil Simiu.Estimating uncertainty in the extreme value analysis of data generated by a hurricane simulation model［J］.J Eng Mech ASCE，2003:1288-1294.

［18］Kirby W H，Moss M E.Summary of flood-frequency analysis in the United States［J］.J Hydrology，1987，96:5-14.

［19］Ochi M K.Stochastic analysis and probabilistic prediction of random seas［J］.Adv Hydro-Sci，1982，13:217-315.

［20］Naffa M G，Fanos A M，Elganainy M A.Characteristics of waves off the mediterranean coast of Egypt［J］.J Coast Res，1991，7(3):665-676.

［21］Quek S T，Cheong H F.Prediction of extreme 3-sec gusts accounting for seasonal effects［J］.Structure Safety，1992，11(2):121-129.

［22］Chowdhury A G，Peng Huang，Jimmy E.Aerodynamic testing application of a full-scale facility for mitigating hurricane-induced coastal disasters［J］.Far East Journal of Ocean Research，2009，2(1):1-27.

［23］刘德辅，史宏达，庞 亮，等. 中国沿海台风灾害区划、防台风标准应急制定、防台风应急评估标准制定［R］. 青岛:中国海洋大学，2008.