海洋立管试验支座设计及其对涡激振动影响研究

李 莹，杨新华，郭海燕，李 朋

(中国海洋大学 工程学院，山东 青岛 266100)

海洋深水立管是海洋油气田开发中一个重要的组成部分，它是连接海上平台和位于海床海底设施的通道。处于海洋环境中的海洋立管所承受的荷载有风、浪、流、冰等。当海流流经立管时，在一定的流速下会产生漩涡脱落，当漩涡脱落频率与结构自振频率接近时，漩涡脱落频率锁定在结构自振频率附近，发生频率锁定现象，引起管道振动加强，从而加快立管的疲劳破坏。

对于海洋立管涡激振动的试验研究，国内外学者做了大量的工作。Chaplin et al［1］在水槽中进行了顶张力立管涡激振动试验研究，试验测得了最高为8 阶模态的涡激振动以及多个模态参与的振动。Trim et al［2］在水池中做了一38 m 长立管的模型拖曳试验，研究了立管的高模态动力响应特性以及不同形式、不同覆盖率的导流板对立管涡激振动的抑振效果。Lie et al［3］在港口海上对顶张力立管模型进行了涡激振动试验，试验的主要目的是测量高长细比下的立管响应模态，试验同时测量了顺流向和横向的涡激振动。国内郭海燕等［4］考虑了管内流体流动，在水槽中做了一个长1.2 m 有内流的立管涡激振动试验，得到内部流体对立管涡激振动的影响规律。张建侨等［5］对28.04 m 柔性立管进行模型拖曳试验，发现较高质量比的立管涡激振动响应频率处于立管自振频率和漩涡脱落频率之间。李琳、付世晓等［6］基于模态分析理论，对柔性立管模型进行了涡激振动试验测试技术研究，验证了用光纤光栅技术进行柔性立管涡激振动试验的可行性及可靠性。

综上所述，对于海洋立管的涡激振动，国内外进行了大量的试验研究。但是同时考虑顶部张力、管道内外流的作用进行两种不同边界条件的立管涡激振动试验研究还未见报道，为了研究不同边界条件对立管涡激振动的影响，设计了铰接、固接两种边界条件下的立管支座，并采用ANSYS 软件对两种支座进行数值模拟及受力分析，最后用于海洋立管的涡激振动试验。试验中，通过变化不同顶部张力、内外流速，对不同边界条件立管的涡激振动规律进行了研究和探讨。

1 试验支座设计及受力分析

1.1 试验支座设计

为了验证铰接和固接不同边界条件下海洋立管的涡激振动规律，设计了铰接和固接两种支座形式。在设计铰接支座中，为满足立管在避免轴向转动的情况下实现顺流向和横向的自由振动，设计中选用深沟球轴承;考虑轴承的基本额定动载荷满足试验载荷的要求，选定合适的轴承，根据轴承的尺寸设计轴承座和轴，两轴之间采取过盈配合;之后设计底座，底座的上端通过螺钉与轴承座连接，下端连接立管，一侧连接软管以便施加内流。铰接支座的顶端是与轴承座连接的上底板，中间留有圆孔用于固定铰接支座和施加顶张力。铰接支座各组成部分装配后如图1 所示。

在设计固接边界条件中，为避免立管的转动，根据铰接支座中的底座的尺寸，设计夹板通过螺钉与底座连接固定，立管的连接及内流的施加与铰接支座相同，夹板的顶端也留有圆孔用于固定固接支座和施加顶张力。固接支座设计各部分装配后如图2 所示。

图1 铰接支座示意Fig.1 Hinged support

图2 固接支座示意Fig.2 Fixed support

1.2 应力与动力特性分析

为了使铰接和固接支座满足试验要求，根据前期设计，在加工之前利用ANSYS 软件对主要受力零件轴和轴承座进行局部应力分析，对铰接支座进行整体应力分析。

1.2.1 局部应力分析

首先进行轴承座的应力分析，用绘图软件Unigraphics NX(简称UG)绘制三维模型图，将UG 三维模型导入ANSYS workbench 后，使用Mechanical 模块，选取材料为结构钢，建立轴承座的ANSYS 有限元模型，建模时简化处理了倒角，对应力集中的部位采用较精细的网格精度。假定底端固定，在轴承座与轴承配合面施加垂直于底面方向大小为250 N 的力(试验预加的最大顶张力)，如图3 所示;通过计算得出轴承座应力分布如图4 所示。由应力图可知，轴承座与轴承配合面处应力较轴承座其它部位大，配合面顶端和与底面平行的断面尤为突出，最大应力处是与底面平行的断面处，应力值为18.2 MPa，远远小于结构钢的屈服极限250 MPa，轴承座的设计符合要求。

图3 轴承座三维模型Fig.3 3D model of bearing block

图4 轴承座应力分布Fig.4 Stress distribution of bearing block

其次进行互相配合的两根轴的应力分析，其中轴A 与轴B 的孔属过盈配合，建立ANSYS 模型，在两根轴端部与轴承配合的端面分别施加反方向大小为250 N 的力，如图5 所示;通过计算得出配合两轴的应力分布如图6 所示。由应力图可知，轴A 的应力分布为由中间与轴B 配合处向两端先逐渐变小，然后在与轴承配合处变大;轴B 的应力分布与轴A 相似。配合两轴最大应力处发生在轴A 上，位于轴A 与轴B 配合面的边缘处，值为123 MPa，小于结构钢的屈服极限250 MPa，可见相互配合两根轴的设计符合要求。

图5 配合轴三维模型Fig.5 3D model of two match-up shafts

图6 配合轴应力分布Fig.6 Stress distribution of two match-up shafts

1.2.2 整体应力分析

在试验中，为了满足试验装置的强度，铰接支座中轴承座与底座的连接处、轴承座与上底板的连接处以及固接装置中夹板与底座的连接处可以采用焊接加强连接强度，所以在分析中去掉底座和底板对整个铰接装置进行应力分析，建立ANSYS 模型，在两对垂直的轴承座底端上分别施加反方向大小为250 N 的力，如图7 所示;通过计算得出铰接装置的应力分布如图8 所示。由应力图可知，铰接装置的最大应力发生在轴A 与轴B 配合面的边缘处，值为118 MPa，小于结构钢的屈服极限250 MPa，因此装配后铰接支座的设计符合要求。

图7 铰接支座三维模型Fig.7 3D model of hinged support

图8 铰接支座应力分布Fig.8 Stress distribution of hinged support

1.2.3 动力特性分析

为了分析支座是否会对立管的动力特性产生较大的影响，分别对有支座和无支座的立管建立ANSYS 模型，其中有支座立管模型中的支座简化为块体采用solid95 单元、材料为钢;立管采用pipe59 单元、材料为铜;无支座立管模型中立管采用pipe59 单元、材料为铜，如图9 和图10 所示。之后在管内外充水、顶张力大小为53.3 N 的情况下，进行模态分析，得出立管一阶、二阶的自振频率如表1 所示。

图9 有支座立管模型Fig.9 Model of riser with a support

图10 无支座立管模型Fig.10 Model of riser without a support

表1 立管自振频率Tab.1 Natural frequency of vibration of risers

由表1 可得，有支座铰接立管比无支座铰接立管的一阶、二阶自振频率大0.001 Hz，有支座固接立管比无支座固接立管的一阶自振频率大0.019 Hz、二阶自振频率大0.05 Hz，说明试验支座对立管自振频率的影响很小，所以支座的设计符合试验要求。

应力分析和动力特性分析符合试验要求之后，按照设计的加工工艺进行机械加工，图11和图12 是加工完成的铰接支座和固接支座。

图11 铰接支座实物照片Fig.11 Finished hinged support

图12 固接支座实物照片Fig.12 Finished fixed support

2 涡激振动试验

本次试验在平面随机波流耦合水池内完成，该水池为60 m×36 m×1.5 m(长×宽×深)，其中有深水井两处，尺寸分别为6 m×6 m×3 m(长×宽×深)和30 m×10 m×5 m(长×宽×深)，本次试验在该大型平面水池的5 m 深井内进行，试验水池改造后可以实现最大流速1.2 m/s，图13 为试验水池。由于试验水池的条件所限，需要设计支撑立管的试验支架，为立管模型提供可靠的支撑，所以设计加工了钢结构支架，支座一端连接立管，另一端连接钢结构支架上，上端通过跨过滑轮的钢丝绳和砝码施加顶张力，通过改变砝码的质量调整顶张力的大小。

试验中采用高压自吸水泵给立管注入内流，采用多谱勒测速仪来测量外流速，试验外流速从0.1 m/s ～1.2 m/s，共变化22 级。试验立管模型采用铜材料，外径为20 mm，壁厚1.5 mm，相关参数如表2 所示。

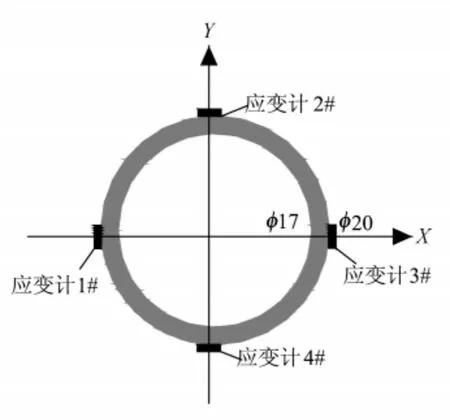
本次试验采用光纤光栅传感器及光信号解调系统来采集数据，如图14 所示，沿立管长度布置12 组应变计，每组4 个，成90°布置，横截面如图15 所示，在X 轴上的两个应变计用来测量顺流向应变，Y 轴上的两个应变计用来测量横向应变，应变计粘贴完毕后涂抹防水胶。

试验外流为均匀流，为防止外流不稳定对立管动态响应的影响，在每级外流速稳定后才开始采样，采样时间为40 s，测量得到随时间变化的应变信号，经数据处理后可以得出立管振动的时程曲线和频谱曲线。

图13 试验水池Fig.13 Experimental pool

表2 立管试验相关参数Tab.2 Related parameters of the risers

3 试验结果分析

为了对比两种不同边界条件对立管涡激振动规律的影响，将顶张力大小为53.3 N、内流流速为0.4 m/s、外流流速分别为0.3 m/s 和0.4 m/s 的两端固定和铰接支座立管8#测点横向振动的时程曲线和频谱曲线绘成图16，由于在这两种流速下固接立管振动功率谱密度远小于铰接立管，为了更直观表达两种边界条件下立管振动频率的不同，图16 中固接立管的功率谱曲线是放大10 倍后的结果。由图可见，当外流速为0.3 m/s 时，铰接立管振动幅值为50 个微应变，振动频率约为3.1 Hz，固接立管振动幅值为20 个微应变，振动频率约为3.62 Hz。铰接立管的振动幅值大于固接立管。当外流流速为0.4 m/s 时，铰接立管的振幅发生了突变，增大到220 个微应变，固接立管则增大到50 个微应变，此时铰接立管的振动频率约为3.25 Hz，接近其二阶自振频率(3.242 Hz)，固接立管的振动频率约为3.64 Hz，铰接立管振幅发生突变的原因是其漩涡脱落频率接近二阶自振频率，发生了锁振现象。

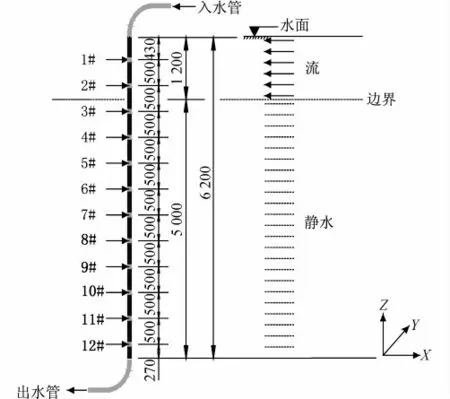
图14 立管试验模型示意Fig.14 Experimental model of risers

将顶张力大小为53.3 N、内流为零、外流流速分别为0.3 m/s 和0.4 m/s 的情况下固定和铰接支座立管沿长度横向位移最大值及均方根值绘成图17。由图可见，当外流流速为0.3 m/s 时，铰接立管进入二阶模态，振动位移的最大值为0.23 D(D 为立管直径)，固接立管仍以一阶模态振动，振动位移的最大值仅为0.11 D，小于铰接立管。当外流流速为0.4 m/s 时，铰接立管以二阶模态振动，振动位移最大值增大为1.05 D，固接立管开始进入二阶模态，振动位移最大值增大为0.32 D，小于铰接立管。

图16 8#测点不同外流速的应变时程和频谱过程Fig.16 Variation of time histories and frequency spectrogram of 8# gauging point with different velocities

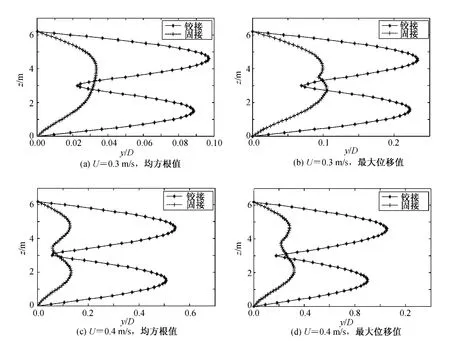
图17 不同边界条件、不同外流时沿立管长度横向位移最大值及均方根值对比曲线Fig.17 Variation of the maximum displacement/diameter and the RMS displacement/diameter of riser with different boundary conditions and velocities

由试验数据分析可以得出，在外流流速为0.3 m/s 时，铰接立管的振幅大于固接立管。当外流速为0.4 m/s时，铰接立管的振幅发生突变，率先出现锁振现象，铰接立管的振幅大于固接立管。此时，铰接立管的二阶振动为主导，振动频率约为3.25 Hz，固接立管的主导振动频率为3.62 Hz。由表1ANSYS 模态分析中铰接立管和固接立管的二阶自振频率分别为3.13 Hz、4.95 Hz，对比可知，试验分析得到铰接立管的振动频率比模态分析的振动频率大0.12 Hz，二者相差较小，说明流速为0.4 m/s 时铰接立管二阶自振频率与漩涡脱落频率相近，已经进入二阶锁振状态。固接立管的振动频率比模态分析的振动频率小1.33 Hz，二者相差较大，说明固接立管尚未完全进入二阶锁振状态。

4 结 语

设计了用于顶张力立管内外流共同作用涡激振动试验的两种支座-铰接支座和固接支座，在两种不同边界条件下进行海洋立管涡激振动规律的试验研究，从数值模拟和试验数据分析中，可以得到以下结论:

1)铰接支座和固接支座符合试验要求，并且能较好的反映铰接和固接两种不同边界条件。

2)顶张力、内流速、外流速相同的情况下两端铰接立管的振动幅值大于两端固接立管;顶张力、内流速相同的情况下，随着外流速的增加，两端铰接立管比两端固接立管率先发生锁振现象，在后续试验中建议使用铰接。

［1］Chaplin J R，Bearman P W，Huera Huarte F J，et al.Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current［J］.Journal of Fluids and Structures，2005，21(1):3-24.

［2］Trim A D，Braaten H，Lie H，et al.Experimental investigation of vortex-induced vibration of long marine risers［J］.Journal of Fluids and Structures，2005，21(3):335-361.

［3］Lie H，Kaasena K E.Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow［J］.Journal of Fluids and Structures，2006，22(4):557-575.

［4］Guo H Y，Lou M.Effect of internal flow on vortex-induced vibration of risers［J］.Journal of Fluids and Structures，2008，24(4):496-504.

［5］张建侨，宋吉宁，吕 林，等.质量比对柔性立管涡激振动影响试验研究［J］.海洋工程，2009，27(4):38-44.

［6］李 琳，付世晓，杨建民，等.运用光纤光栅传感器的涡激振动测试技术［J］.振动、测试与诊断，2011，31(6):728-732.

［7］Vikestad K，Halse K H.Effect of variable current on vortex-induced vibrations［C］//Proc.of 10th Int.Offshore and Polar Engineering Conference.2000，3:493-498.

［8］Zhang Y B，Meng F S，Guo H Y.Experimental investigation of vortex-induced vibration responses of tension riser transporting fluid［C］//Proceedings of the ASME 28th International Conference on Ocean，Offshore and Arctic Engineering.2009.

［9］唐国强，吕 林，滕 斌，等.大长细比柔性杆件涡激振动实验［J］.海洋工程，2011，29(1):18-25.

［10］张永波.深海输液立管涡激振动预报及抑振技术研究［D］.青岛:中国海洋大学，2011.