半潜式平台动力定位系统推进器失效时域模拟

孙丽萍，陈 静，吴宝昌，刘 雨

(1.哈尔滨工程大学 深海科学与技术创新引智基地，黑龙江 哈尔滨 150001;2. 江苏熔盛重工有限公司，江苏 南通 226532;3.交通部上海打捞局海洋工程部，上海 200090)

动力定位系统的诞生与发展逐步改变了人们面对丰富的深海油气资源只能望洋兴叹的局面。由于弥补了传统锚泊系统定位方式的不足，船舶动力定位系统应运而生并得以普遍应用。动力定位系统的基本设计要求就是初步确定动力定位系统的等级和定位能力，这是对动力定位系统进行总体方案设计与技术分析的首要任务。

船体发生机械或技术故障后极有可能最终导致推进器失效并引发严重后果。为保证船舶作业的可靠性、设备和人员的安全，各大船级社对2 级或以上等级的DP 系统提出了进行故障模式和影响分析(FMEA)的要求。FMEA 的目的在于说明与动力定位系统功能有关设备的不同故障模式及其对船舶瞬态影响和剩余定位能力的影响。

各大船级社对DP 系统等级的划分较为一致，但对定位能力的评估差异颇大。DNV 采用环境规则指数(ERN)，LR 选择了能力实现等级(PCR)，而BV 推荐环境位置保持指数(ESKI)对DP 系统附加标志进行增补。以上技术指标均是对DP 系统定位能力的静态分析和验证，而对平台运动进行时域模拟的优点在于，能顾及到更多的环境因素和限制条件，以更接近实际情况的条件下，获得某时间段内平台的位移、速度、推进器功率等有价值的信息［1］。目前对推进器失效的研究集中于失效后的稳态系统定位能力分析，而这里编制的模拟仿真程序更多地关注推进器失效后的平台瞬时响应。

1 水平运动方程

建立完整而合理的平台运动数学模型是进行平台响应分析的先决条件。平台在复杂的环境载荷和DP系统的联合作用下，时刻处于位置的偏离与纠正的反复循环中。这里选取的研究对象为一座配备八个全方位推进器的半潜式深水钻井平台，平台的水下部分外形及推进器布置见图1。将平台看成是一个具有一定质量和质量分布的刚体，利用动力学理论推导浮体在随船坐标系中的运动方程。为了简化运动方程，在研究平台运动时，把船体坐标系的原点设在浮体重心处，如此可得到某时刻i 的运动方程如下［2］:

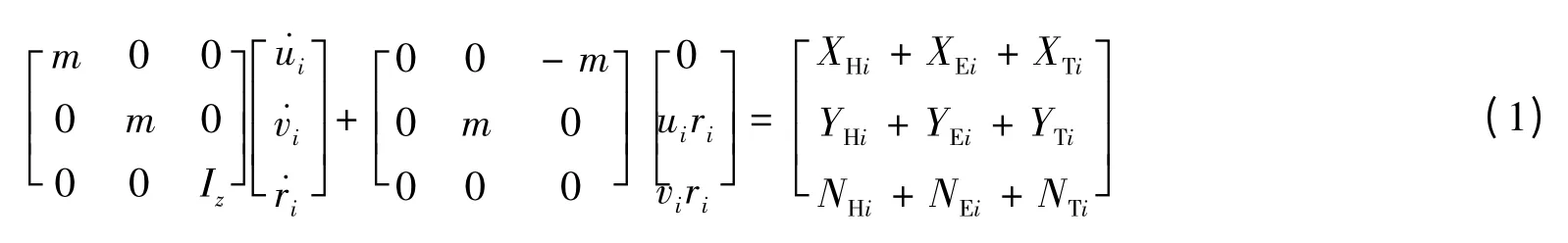
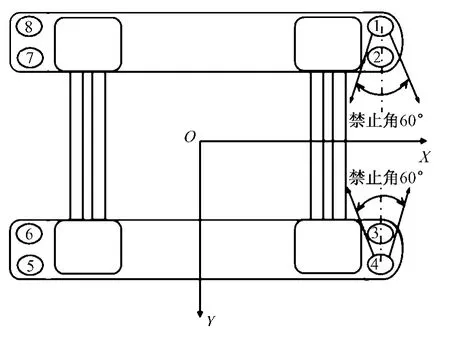
图1 平台水下部分外形及推进器布置示意Fig.1 Schematic of underwater part of the platform and thrusters layout

式中:m 为平台质量，Iz为平台绕Z 轴旋转的转动惯量，下标H，E 和T 分别表示作用于平台的水动力、环境载荷及推进器推力。

由于垂向外力(力矩)具有量级大、周期短的特点，为减小推进器机械及燃油损耗，DP 系统往往仅对低频水平运动做出即时响应。平台的低频运动在很大程度上是受DP 系统控制的，故而在研究平台运动时，假设浮体受到外力作用后在平衡位置作小幅度运动，进而可以在平衡位置附近对平台的运动作简化处理:

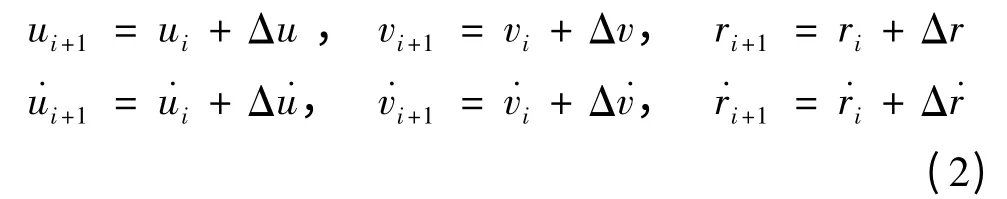
将式(2)代入式(1)，由于运动参数的增量较小，所以参数的高次幂ΔuΔv 和ΔvΔr 被认为是高阶微量，可以忽略。此外，在求解水动力时，忽略与平台速度及角速度间的交叉耦合项及它们的二次项及引起的流体惯性力(矩)，得到:

式中:Xu，Yv，Yr，Nr和Nv为水动力导数(由于平台水下部分关于XOZ 平面对称而并非完全对称于YOZ 平面，所以纵荡运动独立而横荡与首摇运动间存在弱耦合)。

2 外载荷计算

环境条件的选取是定位能力计算的重要基础。拟定平台的主要工作海域为中国南海，但为不失一般性也兼顾考虑了全球其他热点海域的海洋环境。表1 给出了风、浪、流联合一致来向下的环境条件，其中风、流的大小及方向按定常处理。表2 给出了平台的主尺度和关键参数。

表1 半潜平台在作业工况下的环境条件Tab.1 Environmental conditions under operation mode

风载荷计算采用API 推荐做法:将平台水线上各部分主要结构离散，根据受风面积及形状计算各部分的载荷并相加，即模块法。同理，流载荷也采用模块法处理:将平台水线下的浮筒和立柱离散分别求取各自的流载荷，而将连接翼作为Morison 杆处理［3］。需要指出的是，由于模块法对实际结构进行了简化，所以得到的只是精度在许可范围内的近似值。

除了考虑长周期变化的风和流载荷外，波浪载荷则只计及其中的低频部分，即波浪漂移力。波浪二阶漂移力包括二阶平均漂移力，二阶差频力及二阶和频力。二阶平均漂移力是二阶波浪力的定常部分，造成平台的稳定偏移。采用BV船级社的水动力软件HydroStar 求取二阶平均漂移力的三个水平分量(纵荡、横荡、艏摇)在0° ～180°的幅频响应算子RAO，然后采用谱分析法来求得平台的二阶平均漂移力。首先，用等间距法把海浪谱离散为N 等份，进而将不规则波转化成若干谐波叠加的形式，每一波频带对应的波频ωi，波幅为Ai。将各谐波的漂移力叠加即得到该海况下总的二阶定常力(矩):

慢漂力通过Newman 简化公式近似求得:

式中:εi为谐波的随机相位角。该方法不适用于浅水水域，且在计算中产生高频成分，可以通过滤波方法将其滤去。而水动力参数计算及时域运动模拟，均取工作水深1 000 m。

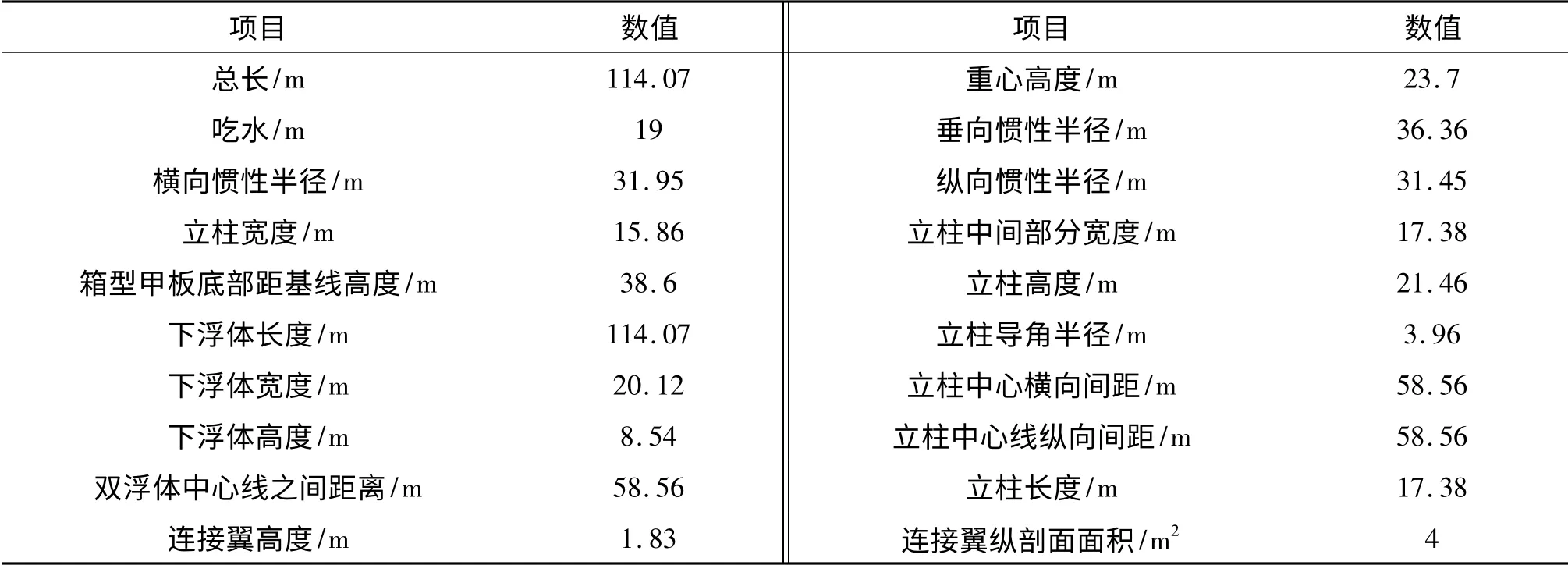
表2 平台的主尺度和关键参数Tab.2 Main dimensions and key parameters of the platform

为了验证HydroStar 软件的运算结果，特此开展了平台运动性能实验研究。实验在综合深水水池进行，水池为50 m×30 m×10 m(长×宽×深)，具有一套75 块摇板的多向造波装置。图2 为平台在不同浪向下水平面运动幅值RAO 的实验值和HydroStar 数值模拟值。由图可以看出，各水平运动分量的数值模拟结果和实验结果在总体趋势上较为吻合，实验结果验证了数值计算结果的准确性，这说明在进行平台受力和运动计算中用到的平台水动力方面的数值计算结果是较为可靠的。

此外，在平台运动时域分析中，对每一时刻计算完成的风载荷，进行前馈处理后结合流载荷和波浪漂移力作为环境载荷项代入方程(3)进行运动求解。处于设计海况下的平台，不同方向下的环境载荷见图3。

图2 不同波频下的平台运动幅值RAOFig.2 The yaw motion RAOs under different frequencies

图3 不同来向下的环境载荷大小Fig.3 The environmental loads from different directions

3 控制器选择及推力分配

深海科学与创新引智基地编制的动力定位时域模拟器DPTDS 能够对安装有DP 系统的浮体运动进行时域分析，尤其对多个不同类型的推进器先后及同时失效时浮体水平运动分量的瞬态响应进行分析。此外，模拟结果可以给出各推进器推力信息、浮体运动信息直观的时历曲线图和统计图。该模拟器采用PID 控制原理和Kalman 滤波技术对浮体进行位置和姿态控制，通过风前馈和拉格朗日优化算法并结合推进器的类型和其机械特性对推进器进行推力分配。

在时域模拟中，由控制器计算得到平台自身需要产生的总推力(矩)，而由推力分配算法结合平台推进器的布置和水动力干扰等因素将总推力合理地分解到各个推进器上，用以抗衡环境外载荷以保证一定程度的定位精度，并使推力系统在定点定位时维持较低功率运行水平以减小消耗。为了顾及实际平台测量系统，计算机控制系统等在数据测量，野点及滤波处理和数据融合方面造成的延迟，模拟中对推力进行分配时，将推力系统发挥效用的时间延迟2 ～4 s，以此来近似模拟动态分配［4］。此外，为了避免全方位推进器尾流的相互干扰，每一个推进器的旋转角度都有一个限制，即禁止角［5］(见图1 所示)。

此处的推进器禁止角根据Nienhuis［4］等人由实验研究结果归纳得出的经验公式得到。Nienhuis 指出位于平板下的推进器，由于平板的存在，推进器尾流会偏向平板，偏离下游推进器进流中心，减弱了对下游推进器的冲击。此时推力损失:

式中:t 为推力损失率;T 为后面推进器的推力;T0为敞水时的系柱推力;x 为两个推进器之间的距离;D 为推进器的直径。显然，对于全回转推进器，可以借助推进器之间的距离和夹角的设置来实现通过控制尾流方向达到减小推力损失的目的。Nienhuis 给出了该情况下的推力损失公式:

式中:φ 为是两桨轴线的夹角(deg);t 为φ=0 时的推力减额因数，可通过式(6)计算;tφ为当夹角为φ 时的推力减额因数。通过式(7)可知，在该推进器布置方案下，当其中一个推进器偏离相邻另一个推进器的角度达到30°时，推力衰减为5%左右，在可接受的范围内。

推力分配是一个多变量有约束的最优化问题。基于优化方法的分配算法将控制分配问题转化为包括目标函数，等式约束和不等式约束的非线性约束优化数学模型，然后利用优化算法对其进行求解。由于平台采用的是全方位推进器，在船体坐标系中，在任何方向αi上(与X 轴的夹角)产生横向力tx，i和纵向力ty，i分量。显然，αi，tx，i和ty，i之间存在以下关系:

为简化问题，将最小总推力等同于最小总功率消耗并建立目标函数:

式中:N 为当前有效推进器的个数。该函数的等式约束:

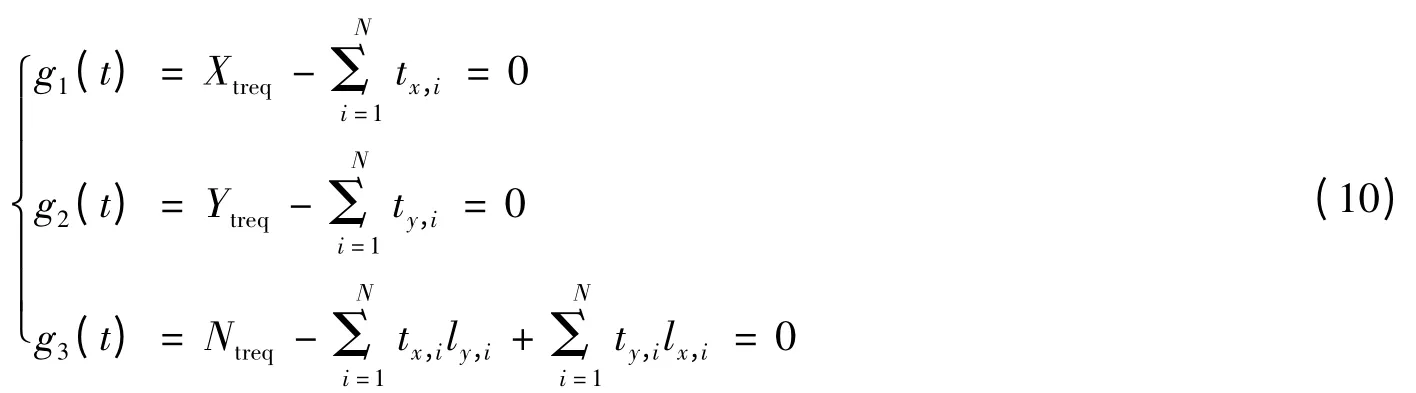
即，由各推进器分量合成的总推力(矩)应与控制器要求的总推力(矩)对等。不等式约束有:

也即，每个推进器的推力不应超过其最大推力。此处的最大推力Tmax，i为考虑了推进器之间、推进器与船体之间干扰的保守值，通常取为推进器最大系柱推力的90%。

禁止角由下述不等式约束实现:

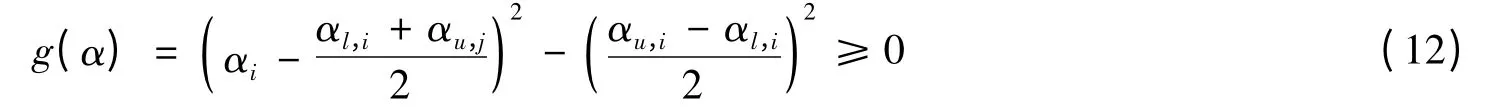
式中:αl，i，αu，i分别为禁止角度区域的下限和上限。

此外，根据推进器的机械特性，在每个时间步内对最大推力变化率以及全方位推进器方向角的转动变化率均作了限制:

当时域模拟时间达到指定的推进器失效时间时，提取变量空间中的瞬时损失的推力分量tx，i和ty，i，将它们归并到下一时间步内推力系统需产生的推力项Xtreq、Ytreq和Ntreq中去，再次进行推力分配。推进器参数详见表3。

表3 全方位推进器参数Tab.3 The parameters of azimuth thrusters

根据以上等式和不等式约束条件，可以成功地将推力分配问题转化为关于自变量t 和目标函数f 的最优化数学问题。

4 时域模拟结果及分析

在模拟的初始时刻，设定平台在地球北东坐标系水平面内有位置和角度偏移(10，10，30°)，并要求平台在随后的模拟中务必保持在离坐标原点(0，0，0°)一定的范围内，以考察平台的位姿回复能力和定点定位能力。限于篇幅，仅就平台在45°斜浪下，1 号和8 号推进器在500 s 和1 000 s 时先后失效后(为最严重的失效模式)的数值模拟结果加以分析讨论。

如图4，模拟的结果显示平台在1 号推进器失效后，8 号推进器失效前并无明显的运动变化，平台能稳定定位于点(－2，－7.7);8 号失效后依然保持一定的水平定位能力，但稳定性明显变差。由图5 给出的平台位移与速度信息来看，进一步验证了:1 号推进器的失效并未引起平台运动的稳定性问题;而8 号推进器在1 000 s 时失效后，各向稳定性都大为降低。在图6 和图7 给出的推进器信息中，可以明显地看到1 号和8 号推进器分别在500 s 和1 000 s 先后失效后，它们将不再启用;其他推进器在1 号和8 号推进器失效后，曲线的波动变大，推力负荷接近饱和。

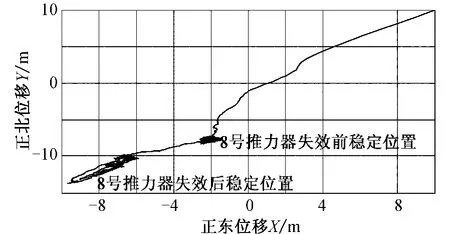
图4 平台的水平运动轨迹Fig.4 The horizontal trajectory of the platform

对模拟程序变量空间内的平台运动和推进器功率变量在200 ～500 s，700 ～1 000 s 和1 200 ～1 500 s内的数值进行统计整理得到表4。从表中的数值上看，1 号推进器失效后虽然使得总功率消耗有较小的增幅但并未导致平台位置的大幅变化，该点与图4 和图5 反映的情况相一致;而在8号推进器也相继失效后，平台的位置发生了较大偏移，而且推进器总功率消耗开始巨幅增加。

图5 平台位移及速度时历曲线Fig.5 Time series of displacement and velocity

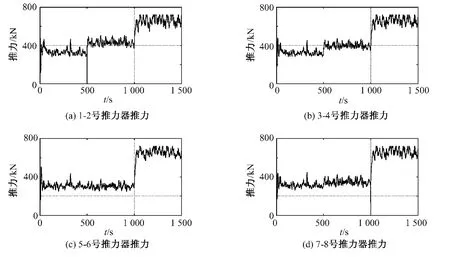
图6 推进器推力时历曲线Fig.6 Thrust time series of all thrusters

图7 推力方向时历曲线Fig.7 Direction time series of all thrusters

表4 平台在不同推进器状态下的运动和功率消耗统计表Tab.4 Statistics of motion and power consumption of the platform under different thruster conditions

5 结 语

从模拟结果看，采用的PID 控制策略能保证部分推进器在指定时间失效后其模拟结果依然具有较好的稳定性、收敛性和快速性。模拟中对推进器推力大小和方向的控制较为契合实际，但对失效后的推进器水动力特性及其对平台运动的影响处理不足，尚待深入研究。此外，该模拟结果也说明了在动力定位过程中，应尽可能让所有的推进器处于低功率水平工作，减小燃油消耗，使动力定位系统具有较好的经济性。

［1］刘 雨. 深水半潜式钻井平台动力定位系统研究［D］. 哈尔滨:哈尔滨工程大学，2010.

［2］API Recommended Practice 2SK，Design and Analysis of Station keeping Systems for Floating Structures［S］.2005:30-36.

［3］Faltinsen O M.Sea Loads on Ships and Offshore Structures［M］.Cambridge:Cambridge University Press.

［4］Nienhuis U.Analysis of thruster effectivity for dynamic positioning and low speed manoeuvring［D］.Delft:Dissertation of Technical University of Delft，1992.

［5］Huijsmans R H M，Bosland R，Dijk J M.Numerical prediction of thruster-thruster interaction［C］//the 28th International Conference on Ocean Offshore Mechanics and Arctic Engineering.2009:OMAE 2009-79744.