涡激致顶张力立管双频参量共振研究
肖 飞,杨和振,卢其进,张黎邦
(1. 上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室,上海 200240;2. Mediterranean Shipping Company Kenny,Houston,TX77084,USA)
海流绕流立管时产生漩涡脱落,会对立管产生涡激力[6,7]。由于涡激力的作用,立管发生横向运动,从而导致轴向张力的不断波动,当张力波动的频率与立管横向振动的固有频率比值满足一定关系时,立管就发生了参量共振(图1 为涡激力引起顶张力立管参量共振的示意图)。由于发生参量共振的马修不稳定性区域是一个个连续的参量区间,因而在深水条件下,立管的横向振动固有频率很可能落入不稳定区域[8,9]。一旦发生参量共振,可导致立管因出现极限应力或显著疲劳而发生破坏,引起管道破裂和流体泄露,造成重大经济损失以及环境污染[14]。因此,避开这类共振是深海立管结构安全设计中的重要要求。

图1 涡激引起顶张力立管参量共振原理Fig.1 Schematic diagram of TTR's parametric resonance by vortex-induced vibration
最初是在模型试验中观察到涡激引起了顶张力立管(Top Tensioned Riser,以下简作TTR)张力波动极值。1998年Huse[1]在空旷海域进行了长90 m、缩尺比约1∶15 的钢制立管模型试验,试验发现涡激引起了大幅轴向张力波动。在随后的理论研究中Huse 指出,如果涡激的频率等于轴向振动一阶模态频率的一半时,会出现极大的轴向应力。1999年Huse[2]经过进一步研究,得到了预测涡激引起深海立管轴向振动更详细的依据,特别是轴向极值响应现象。
API 规范[3]中指出,对于具有张紧器的立管,其遭受相对于平均张力而言相当大的张力波动,由此导致横向刚度明显改变,并且对于这类立管的分析必须考虑轴向张力和横向刚度的耦合。张[4]由TTR 轴向和横向非线性耦合的梁柱方程推导出马修方程,然后基于马修不稳定性理论,研究和解释涡激振动引起TTR张力以两倍于涡激频率波动这一现象,指出深海立管易处于马修不稳定性区域。张[5]还指出在立管设计过程中,如果不考虑涡激振动引起马修不稳定性,这一现象反过来又会增大立管轴向应力和疲劳破坏。故研究涡激致参量共振对立管安全设计意义重大。
目前深海结构参量共振的研究得到众多研究人员关注,但国内外研究大都基于单频激励。张[9]采用希尔无穷行列式法研究了波浪力作用于张力腿平台的TTR 参量共振问题。Chandrasekaran[10]进一步探讨了张力腿平台设计外形和吃水变化,引起立管张力幅值变化的马修不稳定性。近期,卢[11]对有缆遥控潜水器的脐带缆母船垂荡现象进行了探讨,研究表明一定条件下类似的大幅横向振动也会发生。Koo[12]探究了由spar 平台大幅深沉运动引起平台纵倾恢复力臂周期性变化导致的参量共振现象,并针对许多不同的情形对一个实际平台进行了系统的模拟和比较,指出阻尼对抑制参量不稳定性非常重要。在傅[13]对深海钢悬链立管触地点进行动力响应分析之后,杨[14]进一步对参量激励下深海立管不稳定性进行了评估,探讨了阻尼影响,给出了不稳定性抑制的若干建议。苏[15]则具体就深海浮式结构物锚泊阻尼的影响参数展开了研究。上述涉及马修不稳定性的研究都是基于单频激励开展,而海流绕流立管时产生漩涡脱落,进而产生对立管的涡激力作用,在实际海洋环境下此作用具有随机性,依赖于立管周围流体动力特性和结构本身的运动[16]。因此,提出多频叠加预测此激励过程,并着重探讨双频激励研究涡激导致TTR 参量共振机理。建立了TTR 横向和轴向运动非线性耦合的梁柱方程,并推导出TTR 系统相应多频激励马修方程,通过布勃诺夫-伽辽金法计算得到双频激励马修稳定性图,并对比分析了单频和双频激励分别预测TTR 参量稳定性所具有的特性,最后结合工程算例探讨了双频激励参量不稳定分析方法在顶张力立管设计过程的应用。
1 基本理论
1.1 顶张力立管的振动方程
顶张力立管(TTR)在海底通过接头与基础相连,海底约束条件取简支,上部与平台连接,设为简支,作如下假设:
1)因为张力大于TTR 自身重量,所以忽略张力沿高度方向的变化;
2)假定波流传播沿同一方向,且流速沿水深的变化为线性;
3)TTR 的刚度和材料性能沿高度方向不变。
根据非线性应变-位移关系,由基尔霍夫假设,可以得到TTR 梁-柱横向运动静力学学方程,在静力方程中引入内力,即得到TTR 梁-柱动力学方程:

式中:M 为单位长度质量,D 为立管外径,h 为立管厚度,ρs为立管密度,ρw为水密度,ρ 为内部液体密度,Ai为立管横截面积。
在海流中,垂直于水流方向的流体力可分为两部分:一个是升力涡激力,一个是TTR 横向运动时受到的拖曳力,其合力如下:

式(3)右边前者为升力涡激力,后者为拖曳力,Cl为升力系数,Cd为水动力拖曳系数,V 是流速。
将T 代入式(1)得到:
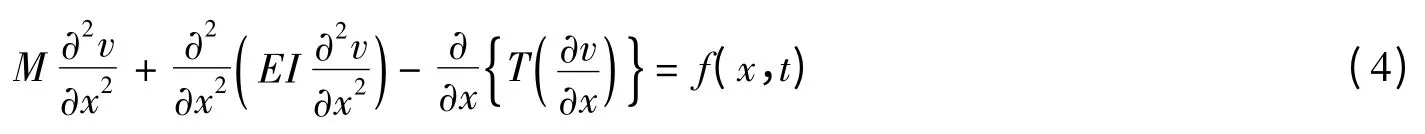

假设张力波动满足如下关系:T=T0+▽Tσ(t),T0为平均张力,▽T 为张力波动幅值。
实际工程问题中,顶张力立管张力波动函数一般并非简单的规则函数,而是多频叠加的不规则函数,即为傅里叶展开的一系列简单函数的叠加:以下将重点研究双频激励最具有代表性的情形,即双频激励情形σ(t)= a2cos2ωt + a4cos4ωt。
1.2 含阻尼项马修方程
假设顶张力立管两端铰接,其n 阶模态解为:
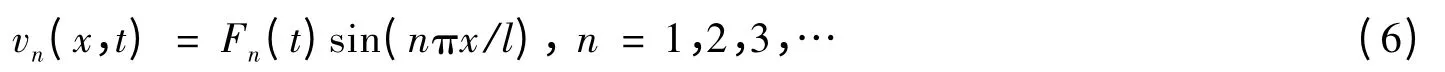
在解φ(t)附近取φ(t)+δφ,带入式(6)得到式(7),通过判断式(7)解的有界性来判断解φ(t)的稳定性。

即得到有阻尼的马修方程:

2 单频和双频参量稳定性对比研究
通过前面对单频与双频激励的实质分析可知,考虑实际外激励,选择双频激励研究涡激引起的顶张力管(TTR)参量共振更为合理。下面对比分析在单频和双频分别激励下TTR 马修稳定性和相应运动响应。
单频:

双频:

式(9)、式(10)分别为单频和双频激励下系统相应的马修方程。图2 是单频/双频激励下稳定性图。

表1 单/双频马修稳定性图中有代表性点特性Tab.1 Property of representative dots in single/bi-frequency Mathieu stability diagram
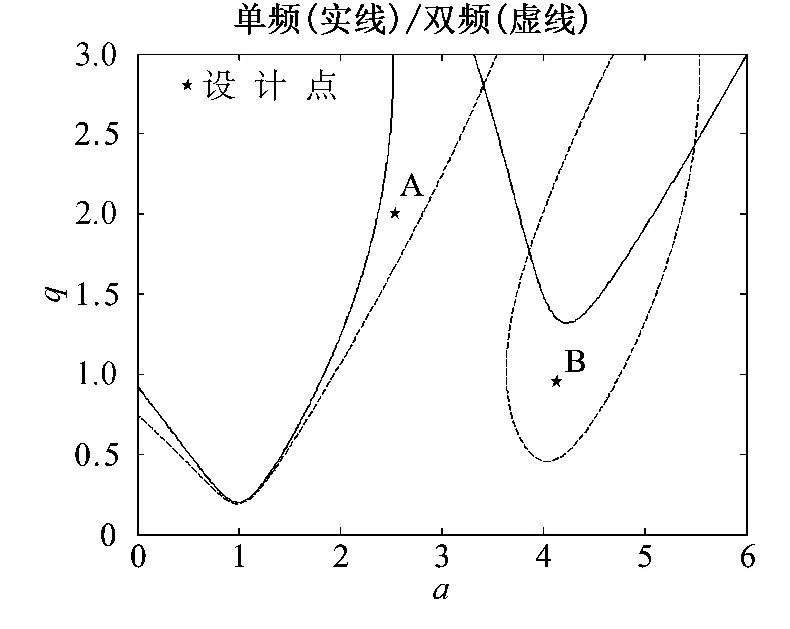
图2 单/双频分别激励下系统马修稳定性Fig.2 Mathieu stability diagram of single/bifrequency induced system
下面以系统动力响应为基础进行分析,在上述区域中选择典型设计点A 和B,具体特性如表1。图3和图4 分别为单频和双频激励下设计点A 对应系统在0 ~500 s 时间内的动力响应特性。图3 单频激励预测TTR 系统不发生参量共振;而图4 双频激励预测TTR 系统发生参量共振,设计点A 对应TTR 系统在短短500 s 内运动幅值增大到1066量级,立管系统将因发生不稳定性破坏而失去正常工作性能。

图3 单频激励下设计点A 运动响应Fig.3 Single-frequency dynamic response at design point A

图4 双频激励下设计点A 运动响应Fig.4 Bi-frequency dynamic response at design point A
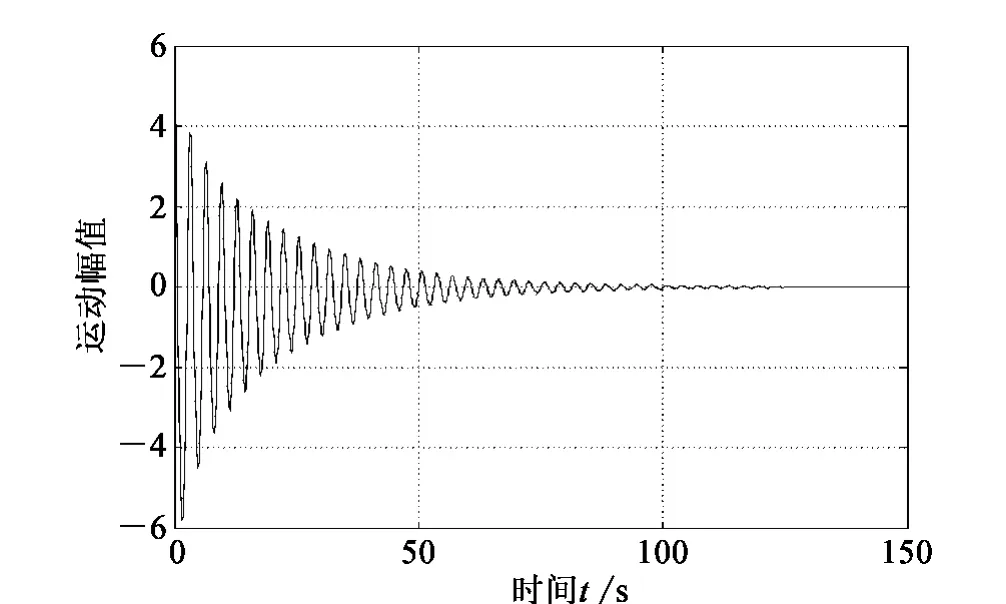
图5 单频激励下设计点B 运动响应Fig.5 Single-frequency dynamic response at design point B

图6 双频激励下设计点B 运动响应Fig.6 Bi-frequency dynamic response at design point B
图5 和图6 分别为单频和双频激励下设计点B 对应系统在0 ~500 s 时间内的动力响应特性。图5 单频激励预测TTR 系统不发生参量共振;而图6 双频激励预测TTR 系统发生参量共振,在短短500 s 内B 点运动幅值增大到1016量级,立管系统同样将因发生不稳定性破坏而失去正常工作性能。上述情形较危险,为避免发生参量共振,实际设计时应选择双频激励函数描述真实外激励,而后根据双频激励预测的系统马修稳定性图,指导设计、调整海洋结构物参数,使得TTR 系统处于双频激励下稳定区域或者通过增大系统阻尼避开不稳定区域。
通过以上研究可以发现,单频激励稳定性图中处于稳定性区域的设计点,在双频激励下有可能处于不稳定性区域。因此,实际指导海洋结构物设计时,采用单频激励对系统马修不稳定性进行预测存在一定危险性;多频激励是对实际随机环境的合理性反映,可用于对实际系统稳定性的预测。
3 算例分析
以工作于墨西哥湾的一个顶张力立管(TTR)为例,系统参数见表2。采用布勃诺夫-伽辽金法求解有阻尼马修不稳定性方程。通过计算得到双频激励马修稳定性图,由此探讨双频激励研究参量不稳定性的特性,最终实现对双频激励下涡激导致顶张力立管参量共振的探讨。

表2 张力腿平台及顶张力立管参数Tab.2 Characteristics of tension leg platform and top tensioned riser
通过对双频激励预测参量稳定性所具有特性的研究发现,激励函数σ(t)=cos2t+dcos4T 中参数d 符号取正、负不同值时,预测的系统稳定性特性有很大差异。因此下面以d= -0.6 和d=0.6 对应的情形为例进行探讨,两种情形下激励函数所对应的时域图形相似,相位相隔π。
此时系统对应的双频激励马修方程为:x″+2cx' +(a+2q(cos2t+dcos4t))=0
立管横向运动最大速度Vmax=1 m/s ,轴向张力变化幅值▽T=1 000 kN,流体阻尼系数Cd=0.6。
3.1 双频激励下立管稳定性
要判定TTR 系统稳定性特性,需要计算系统在n 阶振动模态下马修方程中参数ωn、a、q、c 值,并观察设计点在稳定性图中的位置,如果系统不稳定需要采取应对措施,具体流程如图10。
根据前面给出的TTR 设计参数,计算立管前12 阶振动模态下系统各参数值ωn、a、q、c,具体见表3。根据表3 得到的阻尼系数,求解d= -0.6 及d=0.6 对应的双频激励马修方程,得到相应稳定性图;为直接观察分析系统此时稳定性,将表3 中系统前12 阶振动模态对应的设计点显示在d= -0.6 和d=0.6 对应的稳定性参量平面,得到图8、图9。图8 为双频激励在d= -0.6 时预测的TTR 系统稳定性图,系统前12 阶振动模态对应的设计点全部处于稳定性区域;阻尼对二阶不稳定区域受影响不显著,故12 个设计点离稳定性过渡曲线较近。图9 为双频激励在d=0.6 时预测的TTR 系统稳定性图,系统前12 阶振动模态对应的设计点也全部处于稳定性区域,阻尼对二阶不稳定性区域的抑制作用较明显,故12 个设计点离稳定性过渡曲线较远。

表3 工程算例马修方程系数表Tab.3 Coefficients of the Mathieu equation of the numerical case

图7 双频激励参量稳定性分析流程Fig.7 Process for analysis of bi-frequency parametric stability
图8 和图9 对TTR 系统参量稳定性的预测,反映出了双频激励研究参量稳定性在d <0 和d >0 两种情形下所具有的特性,即d <0 和d >0 对应的双频激励反映的稳定性有较大区别,尤其在二阶不稳定区域。当d >0 时,阻尼使二阶不稳定区域大幅衰减,而d <0时衰减效果相对较弱。符号相反绝对值相等的两个参数d,其激励函数时域图形相似、相位相隔π,而它们对同一系统稳定性的预测却有较大差异。因此,实际立管设计分析,预测外激励的激励函数选取很重要。
3.2 系统阻尼设计
当系统参数设计落在参量平面不稳定性区域时,引入额外阻尼可以抑制不稳定性而避免发生参量共振。因此在顶张力立管(TTR)设计时,如何选择系统参数确定系统阻尼,使得立管能够经受一定的极限情形而不致出现不稳定性,是一个很重要的问题。具体分析对应于立管轴向张力波动的几个极限情形下系统阻尼的设置:给出▽T =5 000、7 000、9 000 kN三种极限情形(在这三种情形下TTR 系统在自身设计阻尼下都是不稳定的),同样在d= -0.6 和d=0.6 对应的两种激励函数情形下,研究系统稳定所需最小阻尼,以使所设计立管避开不稳定区域。具体比较数据见表4。

图8 算例在双频激励下的稳定性(d= -0.6)Fig.8 Bi-frequency Mathieu stability diagram for the engineering case (d= -0.6)

表4 三种极限状态下系统稳定所需最小阻尼Tab.4 The smallest damping of the system for keeping stable under three extreme cases
参数d 符号相反绝对值相等时,其对应的双频激励对系统稳定性预测的差异性,在上一小节做了定性分析;这一小节对此差异性从阻尼选取角度做定量分析。分析表4 可知,在TTR 轴向张力变化三种极限状态下,d= -0.6 预测的维持系统稳定所需的最小阻尼都比d=0.6 的情形大,而且二者在数值上相差很多。
在工程实际的立管设计中,选择d <0 对应的激励函数来预测系统所需要的阻尼,更偏于保守和安全。而工程设计中,增加额外阻尼会相应增大系统设计成本。因此,预测外激励的激励函数选取很重要;实际指导立管设计时,应合理且慎重地考虑双频激励函数形式的选择,以确定相对合理的设计方案。
4 结 语
根据顶张力立管(TTR)的结构特性及海洋环境下的动力特性,建立了TTR 轴向和横向非线性耦合运动的梁柱模型,推导出马修不稳定方程探讨涡激致TTR 参量共振的激励。通过与单频激励研究TTR 参量稳定性分析,探讨了双频激励预测TTR 系统参量稳定性问题的合理性,最后结合工程算例讨论了双频激励应用。研究发现:
1)单频和双频激励分别预测TTR 系统的参量共振,二者得到的系统马修稳定性有很大差异;单频激励稳定性图的稳定区域,在双频图中可能处于不稳定区域;如果选择单频激励下的稳定区域指导TTR 设计,而此选择又处于双频下不稳定区域,将导致立管发生参量共振,使系统发生剧烈不稳定性响应而导致破坏。
2)实际指导工程设计时,预测真实外激励的激励函数选取很重要,其函数形式决定了系统参量稳定性特性以及系统阻尼设计,由此影响到系统设计成本问题。
[1]Huse E,MARINTEK,Kleiven G,et al.Large scale model testing of deep sea risers[C]∥Proc.of 1998 Offshore Technology Conference.Houston:[s.n.],1998:189-198.
[2]Huse E,MARINTEK,Kleiven G,et al.VIV-induced axial vibrations in deep sea risers[C]∥Proc.of 1998 Offshore Technology Conference.Houston:[s.n.],1999:978-986.
[3]American Petroleum Institute.Design of Risers for Floating Production Systems (FPSs)and Tension-Leg Platforms(TLPs)[M].Washington:American Petroleum Institute,2006.
[4]Zhang L B,Eltaher A,Jukes P.Mathieu instability of TTR tension fluctuation due to VIV[C]∥Proc.of the 5th International Offshore Pipeline Forum.Houston:[s.n.],2010:IOPF 2010-2002.
[5]Zhang L B,Eltaher A,Jukes P.Engineering application of riser mathieu instability and axial stress fatigue due to VIV[C]∥Proc.of the 6th International Offshore Pipeline Forum.Houston:[s.n.],2011:IOPF 2011-4001.
[6]Mestanzade N,Yilmaz L.Vortex sheddings on the instability at subsea suspended pipeline[C]∥Proc.of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril:[s.n.],2008:15-25.
[7]Rao Z B,Fu S X,Yang J M.Votex-induced vibration analysis of steel catenary riser[J].Journal of Ship Mechanics,2011,15(3):245-258.
[8]周纪卿,朱因远.非线性振动[M].西安:西安交通大学出版社,1998.
[9]Zhang L B,Zou J,Huang E W.Mathieu instability evaluation for DDCV/SPAR and TLP tendon design[C]∥Proc.of the 11th Offshore Symposium.Houston:[s.n.],2002:41-49.
[10]Chandrasekaran S,Chandak N R,Anupam Gupta.Stability analysis of TLP tethers[J].Ocean Engineering,2006,33(3-4):471-482.
[11]卢其进,杨和振.母船垂荡导致ROV 脐带缆参量共振的研究[J].海洋技术,2011,30(3):77-82.
[12]Koo B J,Kim M H,Randall R E.Mathieu instability of a spar platform with mooring and risers[J].Ocean Engineering,2004,31(17-18):2175-2208.
[13]傅俊杰,杨和振.深海钢悬链立管触地点动力响应分析[J].海洋工程,2009,27(2):36-40.
[14]Yang H Z,Li H J.Instability assessment of deep-sea risers under parametric excitation[J].China Ocean Engineering,2009,23(4):603-612.
[15]苏志勇,陈 刚,杨建民,等.深海浮式结构物锚泊阻尼参数研究[J].海洋工程,2009,27(2):21-28.
[16]Chen W M,Li M,Zheng Z Q,et al.Dynamic characteristics and VIV of deepwater riser with axially varying structural properties[J].Ocean Engineering,2012,42:7-12.

