斜坡堤波浪爬高和越浪数值模拟
杨锦凌,孙大鹏,吴 浩,李玉成
(1. 海军工程设计研究局 工程综合试验研究中心,山东 青岛 266100;2. 大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116023)
斜坡堤是保护沿海地区免受波浪袭击的重要工程设施,斜坡堤上的波浪爬高和越浪一直是各国学者研究的热点。而影响斜坡堤上波浪爬高和越浪的因素比较复杂,主要包括平台宽度、平台超高、堤顶超高、波陡、斜坡堤坡度和相对水深等因素。近几十年来,国内外学者对斜波堤的越浪已经做了大量的研究工作,Saville[1]进行了规则波在斜坡堤上的越浪量模拟实验;贺朝敖等[2]通过在实验室的物模试验基础上总结了一些斜波堤越浪的规律。另外一些学者如王永学[3]采用N-S 方程和VOF 方法实现了无反射数值波浪水槽;王本龙和刘桦[4]建立的数值波浪水槽发展了一种解析-松弛造波、消波方法;周勤俊[5]、刘亚男[6]以及王鹏[7]等通过建立数值波浪水槽,开展了斜波堤爬高和越浪方面的数模研究工作。
基于FLUENT 软件平台[8],采用N-S 方程的k-ε 湍流模型和有限体积法,从造波、消波出发,通过在动量方程中添加不同的源函数,增置了源函数造波方式下的无反射造波模块,实现了适用于VOF 方法的无反射数值造波以及水槽末端的消波,并验证了数值波浪水槽的消波有效性。建立的数值波浪水槽,奠定了斜坡堤上波浪爬高和越浪等后续深入研究工作的基础,同时亦可供斜坡堤工程设计参考所应用。
1 数值波浪水槽
控制方程包括连续性方程和动量方程:
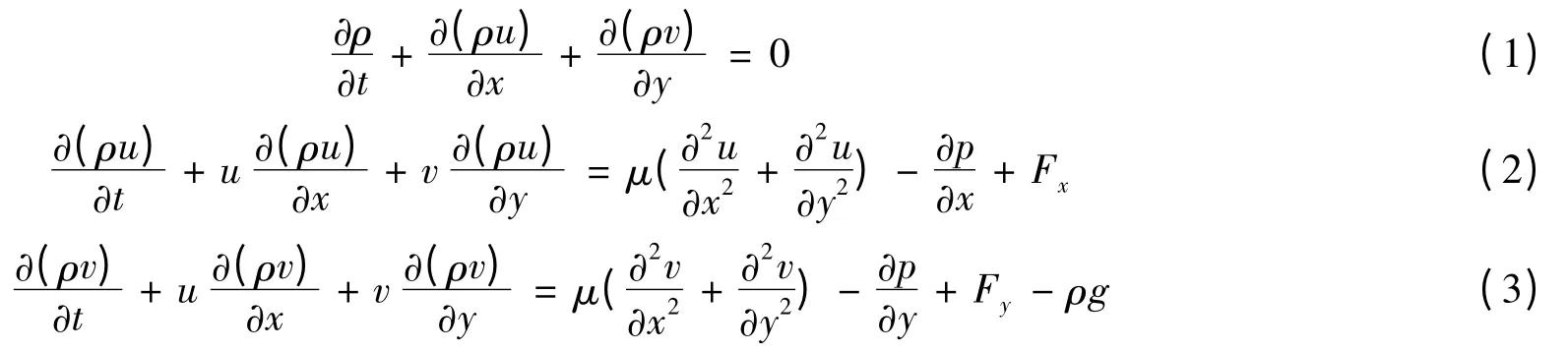
式中:u 为x 方向速度,v 为y 方向速度,μ 为动力粘性系数,p 为压强,g 为重力加速度,Fx和Fy分别是x 和y方向的附加动量源项。

图1 数值波浪水槽Fig.1 Numerical wave sink
数值波浪水槽如图1 所示,水槽从左至右依次为造波区、前端消波区、工作区以及末端消波区等功能设置区。以下标m、l、j 分别代表离散值、来波值和计算值,下标xmin 和xmax 分别为各区域左边和右边坐标值。C=C(x)为与空间位置有关的光滑过渡函数,则:
在造波区: um=cul;vm=cvl;pm=cpl;其中[c]xmin=0;[c]xmax=1。
在前端消波区: um=cuj+(1 -c)uj;vm=cvj+(1 -c)vl;pm=cpj+(1 -c)pl
其中:[c]xmax=0;[c]xmax=1。
在尾端消波区: um=cuj;vm=cvj;pm=cpj。其中:[c]xmax=1;[c]xmax=0。
将以上各区域的速度和压力表达式代入连续性方程(1)和动量方程(2)和(3)后,得到水槽中各功能设置区内的动量源项为:
造波区:

前端消波区:

末端消波区:

将以上各区域的源项式(4)~式(9)用C 语言编译,通过FLUENT 软件的UDF 接口分别代入到动量方程式(2)~式(3)中,压力项采用SIMPLE 算法,自由面采用几何重构法,进而实现水槽中各功能设置区的造波、消波。
2 数值水槽消波的实现及有效性的验证
为探讨数值水槽的造波稳定性和消波的有效性,采用波高为0.3 m、周期为2 s 的试验波要素,设定一种数值水槽长度为220 m,水深为1 m,后文简称“数值水槽1”;设定另一种数值水槽长度为52.4 m,水深为1 m,后文简称“数值水槽2”。
1)以往建立的数值波浪水槽大多是通过加大水槽试验段的长度,在波浪遇建筑物形成的反射波再次到达造波边界之前停止计算来达到避免水槽中二次反射波的目的。利用此方法虽然规避了二次反射波,但是由于加大了水槽试验段长度,一方面增加了计算时间,另一方面也会因水槽加长而导致波浪沿程衰减现象的加剧,图2 为“数值水槽1”中距造波区右边界不同位置处的波形图。由图2 可知距造波源处越远,波浪衰减越明显。因此,依据此方法而建立的数值波浪水槽无法实现长序列波数值模拟的高效性和精确性。
2)水槽末端消波有效性的验证:依据本方法在“数值水槽2”的末端消波区中添加消波源项,当水槽末端实施消波时,在水槽中间20 及40 m 处监测波面,同线性波理论解相比如图3 所示。与图2 相比,依据本方法建立的能够造波、消波的数值波浪水槽,由于减小了水槽试验段的长度,波浪的沿程损失随之减小,并得到了长历时的稳定波浪。
3)验证水槽造波端消波的有效性:将“数值水槽2”右边界设为直立墙边界时,在前端消波区中添加消波源项,遇直墙后入射波与反射波相叠加,在水槽中将会形成驻波,如图4(a)为在不同时刻水槽内的波面空间过程线,图4(b)为水槽52.4 m 处(即水槽右边界)的波面时间过程线,图4(c)和4(d)分别为波腹和波节点处波面随时间变化曲线,即在反射波到达之前是入射波的波形,反射波到达之后形成了波腹和波节点所特有的波形。
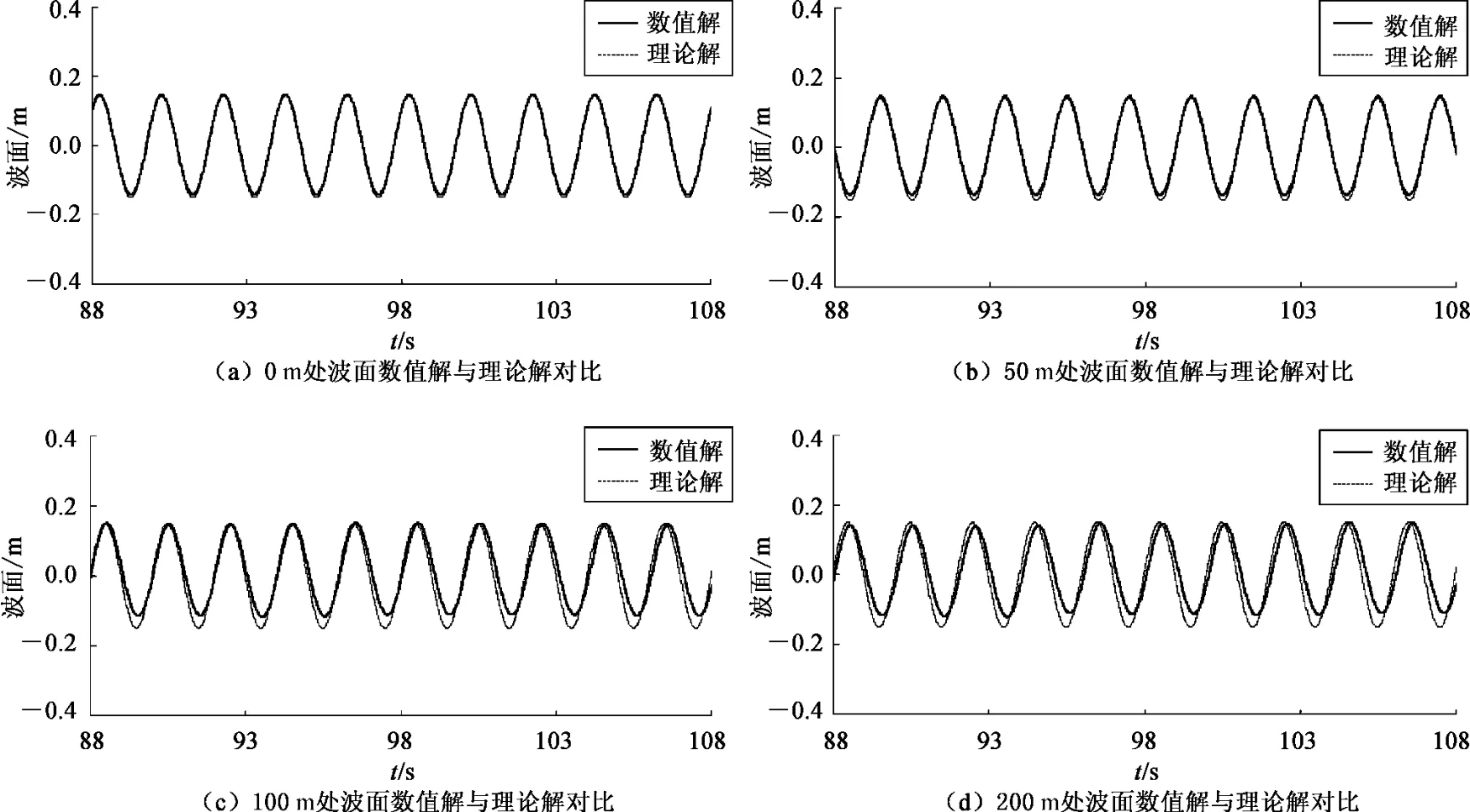
图2 不同位置处波面数值解与理论解的比较Fig.2 Comparison of numerical and theoretical waves at different locations
综上数值计算结果可知水槽末端消波区和前端消波区均能有效工作,水槽中波浪沿程衰减严重的现象得到改善,并且能够实现长序列波,因此本文建立的数值波浪水槽实现了计算的高效性和精确性。

图3 不同位置处波面数值解与理论解对比Fig.3 Comparison of numerical and theoretical waves at different locations
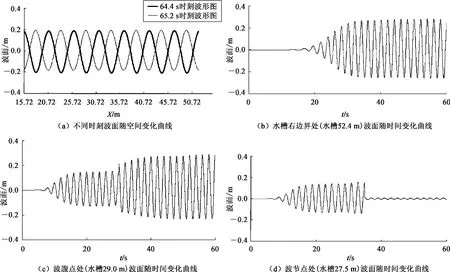
图4 水槽驻波波面示意Fig.4 Standing wave of sink at different time
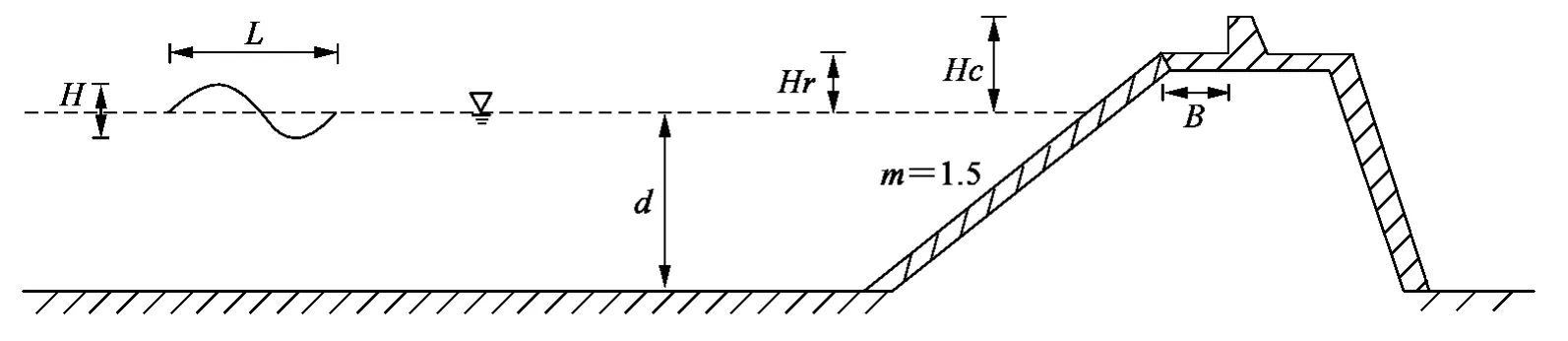
图5 斜波堤断面示意Fig.5 Sloping dike section
3 斜坡堤越浪
越浪关系到斜坡堤工程的断面稳定性,因此设计斜坡堤时需要考虑越浪量对斜坡堤的影响。贺朝敖[2]做了平台宽度B、平台超高Hr、堤顶超高Hc、波陡H/L、坡比m 和相对水深d/H 等因素影响下的斜坡堤越浪实验,总结了在各因素影响下越浪量的变化规律,其所采用的斜坡堤断面如图5 所示。本文依据文献[2]的物模实验模型,对平台宽度以及平台超高对带胸墙斜坡堤越浪的影响进行了数值模拟,并与文献[2]结果做了对比。
3.1 平台宽度对越浪量的影响
文献[2]的斜坡堤护面块体为二层扭工字块,查《海港水文规范》[9]得糙渗系数K△=0.38,当利用FLUENT 模拟斜坡堤越浪量的影响实验时,由于FLUENT 没有糙渗系数,只有惯性阻力系数,对于图5 所示斜坡铺设的护面块体,将其设置为多孔介质区域,多孔介质模型的源项表达式为:

式(10)的右端第一项为层流粘性损失部分,第二项为惯性阻力损失部分,其中1/α 为粘性阻力系数,C2为惯性阻力系数。忽略粘性阻力,将惯性阻力部分作为多孔介质模型的动量耗散源项[7],模拟不同惯性阻力系数C2下的爬高历时曲线,由爬高值分析得出惯性阻力系数C2和糙渗系数K△之间的关系,进而达到模拟铺设护面块体的斜坡堤越浪的目的。
针对不同平台宽度下的斜坡堤越浪量,依照文献[2]所采用波要素(H=0.32 m,T=2.33 s)模拟出各爬高值r 与光滑斜坡护面的预报爬高值R 比值,即r/R 为糙渗系数K△,不同惯性阻力系数下波浪爬高历时曲线如图6 所示,通过数据分析,发现糙渗系数K△与惯性阻力系数C2呈二次曲线关系,绘制曲线如图7 所示,由曲线读取惯性阻力系数C2=1.32。进而在H/L =1/20、Hr/H =0、d/H =3.1、m =1.5 以及惯性阻力系数C2=1.32 的条件下,采用本文的数值水槽计算了斜坡堤不同平台宽度(B/L=0,0.05,0.11)越浪量随时间的过程曲线如图8 所示,本文计算结果与文献[2]物模实验结果如表1 所示,将表1 数据绘制在图9 的坐标中。
由表1 和图9 可知:数模计算值与物模实验值的规律性一致且接近,即随着平台宽度加大,越浪量减小;随着堤顶超高增高,越浪量减小,说明基于FLUENT 平台开发的具有消除二次反射波功能的数值水槽能够保持很高精度模拟不同平台宽度下斜坡堤的越浪量。
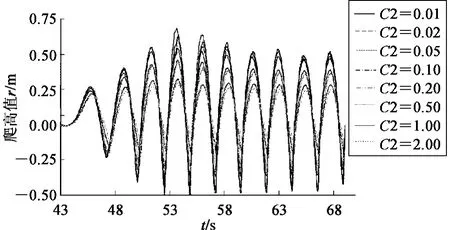
图6 不同C2 值下的爬高历时曲线Fig.6 Duration curve of run-up in different C2

图7 惯性阻力系数的对数C2 与糙渗系数K△的关系Fig.7 The relationship between C2 and K△
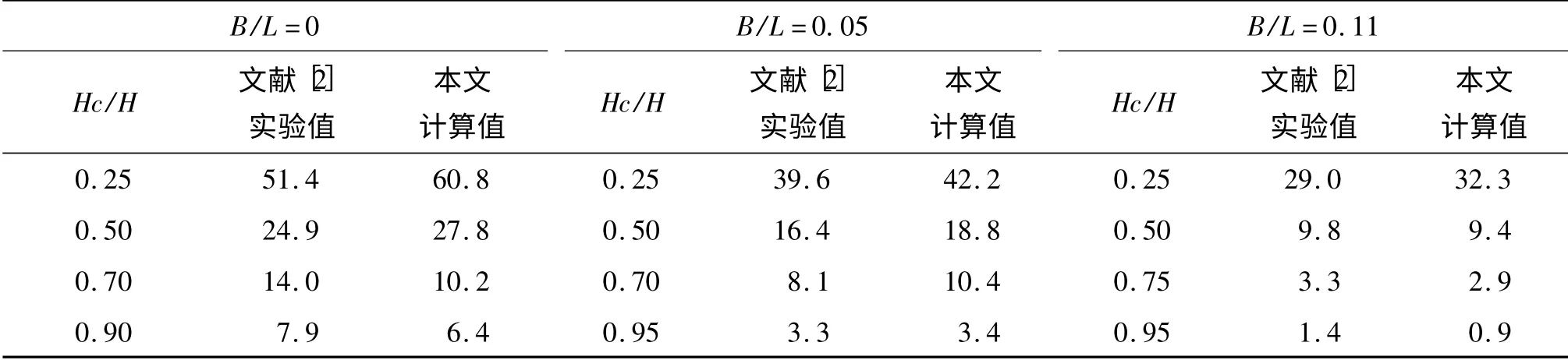
表1 不同平台宽度下文献[2]及本文越浪量 10 -3 m3/(m·s)Tab.1 Wave overtopping flux under different platform widths 10 -3 m3/(m·s)
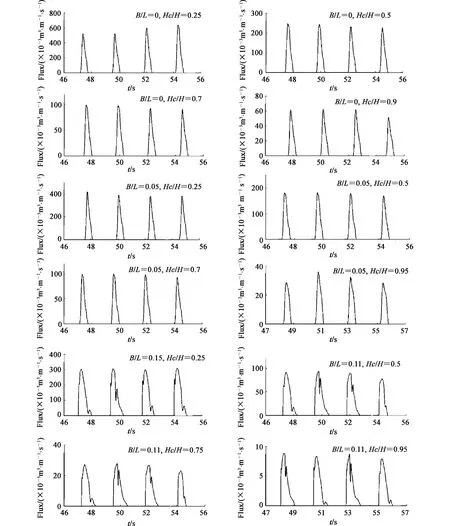
图8 不同平台宽度的越浪量历时曲线Fig.8 Duration curve of overtopping flux under different platform widths
对图9 所示的越浪量进行拟合,得出无量纲公式为:
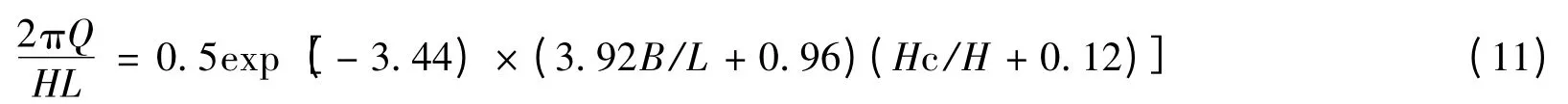
式(11)反映出越浪量随着平台宽度B/L 的增大而减小,随着堤顶超高Hc/H 的增加而减小。
3.2 平台超高对越浪量的影响
为探讨平台超高对越浪量的影响,依据文献[2]所采用的模型及波要素(H =0.32 m,T =2.33 s),在H/L=1/20、B/L=0.05、d/H=3.1、m=1.5 的条件下,采用本文的数值水槽模拟带胸墙斜坡堤的越浪,由于本次计算所采用的波要素与不同平台宽度对带胸墙斜坡堤越浪影响时的波要素相同,因此要模拟的斜坡面惯性阻力系数同样为C2=1.32。分别采用两种平台超高(Hr/H=0,0.5),模拟得到不同平台超高下斜坡堤越浪随时间的过程曲线如图10 所示。
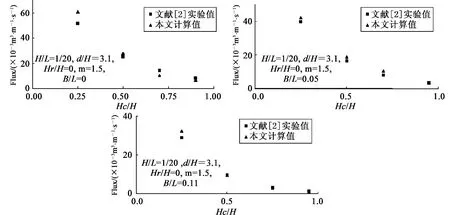
图9 不同平台宽度下本文与文献[2]越浪量比较Fig.9 Comparison of wave overtopping flux under different platform widths
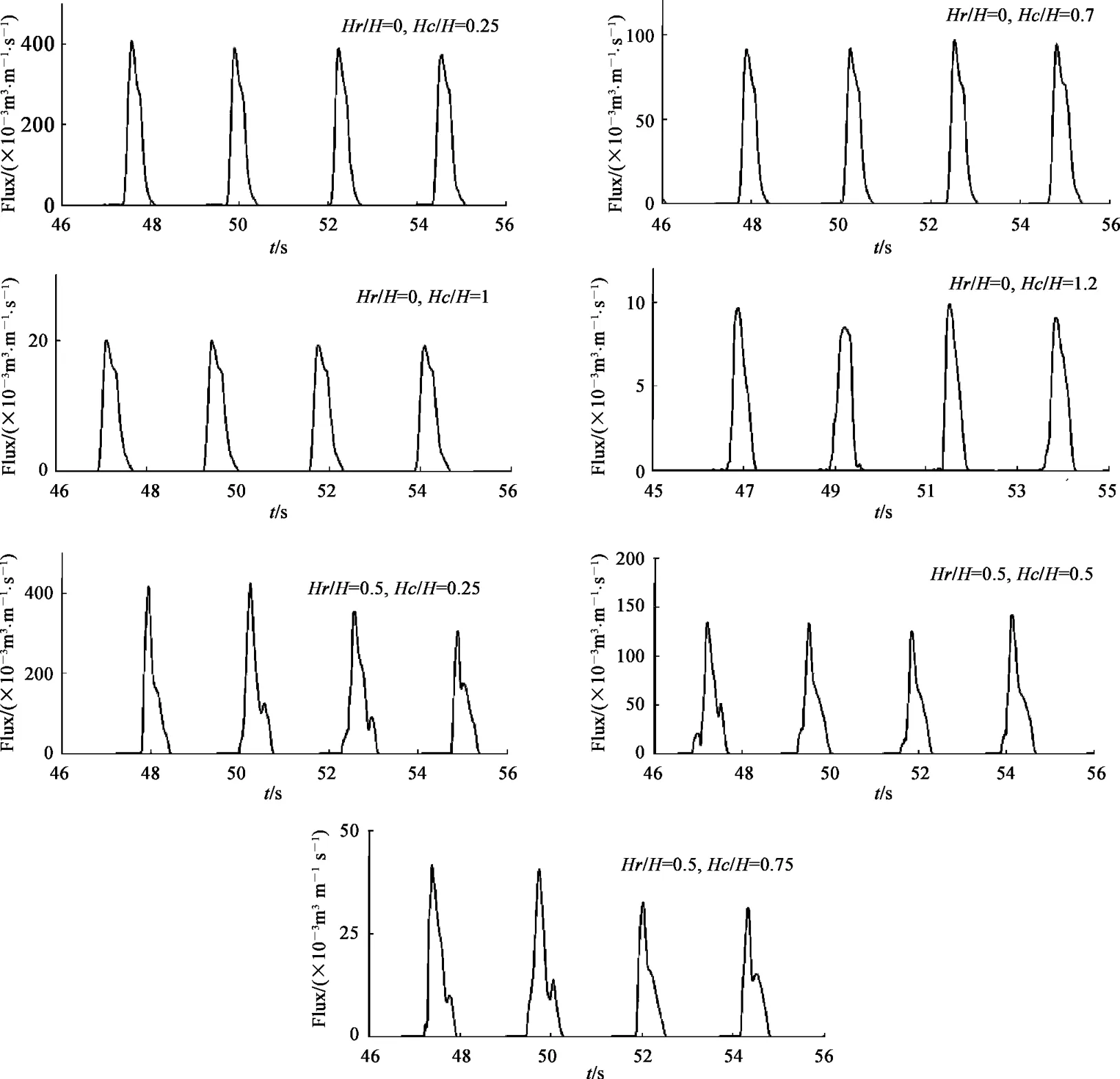
图10 不同平台超高下越浪量历时曲线Fig.10 Duration curve of overtopping flux under different platform heights
本文计算越浪量与文献[2]物模实验结果列于表2 中,将表2 数据绘制于如图11 所示的坐标中。由表2 和图11 可知:数模计算值与物模实验值的规律性一致且接近,即随着平台超高加大,越浪量减小,消波效果更好;随着堤顶超高增高,越浪量减小,说明基于FLUENT 平台开发的具有消除二次反射波功能的数值水槽能够保持很高精度来模拟不同平台超高下斜坡堤的越浪量。

表2 不同平台超高下文献[2]及本文越浪量 10 -3 m3/(m·s)Tab.2 Wave overtopping flux under different platform heights 10 -3 m3/(m·s)

图11 不同平台超高下本文与文献[2]越浪量比较Fig.11 Comparison of wave overtopping flux under different platform heights
对图11 所示的越浪量进行拟合得出无量纲公式如下:
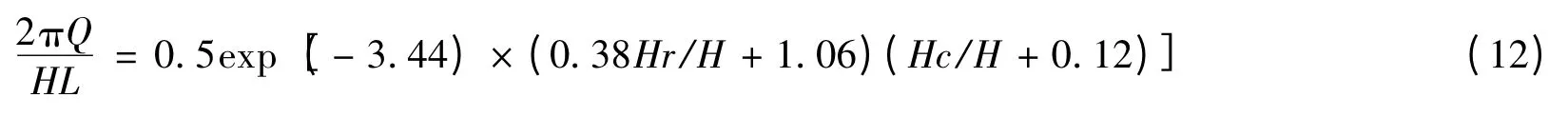
式(12)反映出越浪量随着平台超高Hr/H 的增加而减小,且随着堤顶超高Hc/H 的增加而减小。
4 结 语
依据连续性方程和动量方程给出了源项表达式,基于FLUENT 平台的二次开发为数值水槽添加了无反射造波和末端消波模块,建立的数值波浪水槽一方面消除了二次反射波的影响,提高了计算的精确性;另一方面消除了以往由于增加水槽长度而带来的波浪沿程损失的影响,提高了水槽的计算效率。在对数值波浪水槽造波以及消除二次反射波验证之后,模拟了带胸墙斜坡堤的爬高和越浪,并与文献[2]的物模实验结果进行了对比,对比显示本文计算值与文献[2]物模实验结果规律性一致,吻合良好,表明本文建立的数值波浪水槽能够较精确地模拟斜坡堤爬高和越浪。同时,基于FLUENT 平台开发的无反射数值波浪水槽能够实现计算的精确性和高效性,为长序列的不规则波等研究工作奠定了基础。
[1]T Saville.Laboratory data on wave run-up and overtopping[M].Lake Okeechobee levee sections,U.S.Army,Corps of Engineers,Beach Erosion Board,Washington,D.C.,1955.
[2]贺朝敖,任佐皋.带胸墙斜坡堤越浪量的实验研究[J].海洋工程,1995,13(2):62-71.
[3]王永学.无反射造波数值波浪水槽[J].水动力研究与进展:A 辑,1994,9(2):205-214.
[4]王本龙,刘 桦.一种适用于非均匀地形的高阶Boussinesq 水波模型[J].应用数学与力学,2005,26(6):1-6.
[5]周勤俊,王本龙.海堤越浪数值模拟[J].力学季刊,2005,26(4):629-633.
[6]刘亚男,郭晓宇.基于RANS 方程的海堤越浪数值模拟[J].水动力学研究与进展:A 辑,2007,22(6):682-688.
[7]王 鹏,孙大鹏,吴 浩.海堤上波浪爬高与越浪计算分析[J].海洋工程,2011,29(4):97-102.
[8]FLUENT 6.0 UDF Manual[M].FLUENT Inc.,2001.
[9]JTJ 213-98,海港水文规范[S].北京:人民交通出版社,1999.

