并列双圆柱涡激振动的经验性模型研究
秦 伟,康 庄,孙丽萍,宋儒鑫
(哈尔滨工程大学 船舶工程学院深海工程技术研究中心,黑龙江 哈尔滨 150001)
由于圆柱体之间的相互影响,双圆柱体的涡激振动机理及现象相对于单圆柱体而言更加复杂。目前,国内外的研究者对双圆柱体的涡激振动机理和现象进行了一定的研究,发现了影响串列或并列排列双圆柱涡激振动特性的主要参数,比如两圆柱体的中心间距、雷诺数以及两个圆柱体的约束方式等。
Zdravkovich[1]对双圆柱的涡激振动受力特性以及尾流形式做了综述性的介绍,同时指出:对于双圆柱体,由于两个圆柱周围流场的相互影响作用,在同一雷诺数下,也会表现出和单个孤立圆柱体不同的振动特性和旋涡脱落现象,而且随着横向和流向间距比的不同,两个圆柱体的尾涡特性和受力特性也会有较大的不同。姚熊亮[2]对均匀流中并列刚性和弹性圆柱的流场进行了分类,同时认为脉动升力和阻力系数与柱的振幅、约化阻尼及两柱间距有关,对柱型结构而言,合理的响应预报模型取决于流体载荷的系统分析。Williamson[3]对并列双圆柱体的尾流特性做了深入的研究,发现两个圆柱体在T/D >2.2 的特定间距比条件下,并列双圆柱体下游的尾涡域内存在平行涡街同步的现象,即两个平行涡街表现为反相位(in anti-phase)或者是同相位(in phase)这两种形式。Sumner[4]也对并列双圆柱体尾涡进行了研究,发现其尾涡模态可能存在3 种形式,分别为单一涡街(Single-bluff-body behaviors)、偏向流动(Biased flow pattern)和平行双卡门涡街(Parallel vortex streets)形式。具体每个影响区域的中心间距会随着雷诺数、实验条件和固定方式等的不同而发生一定的变化。Wang[5]发现当并列排列的两个圆柱体之间的中心间距比为1 <T/D <1.1 ~1.2 时,两个圆柱体可以基本看成一个圆柱体,出现单个卡门涡街。Sumner[4]研究发现在雷诺数Re=1 000 ~3 000,中心间距比T/D=1.5 时,出现了偏向流动的现象,圆柱体出现不对称的尾流运动和高频率的旋涡脱落模态,其中一侧的尾涡脱落频率是另一侧的脱落频率的倍数关系,同时Sumner 还指出在T/D =2.5 和T/D =4.5 时发现了并排双卡门涡街现象,此条件下两个圆柱体相互影响比较小,同时两圆柱体的旋涡脱落频率相当。
由于涡致双圆柱振动的过程比单圆柱情况更加复杂,公开发表的有关预报双圆柱涡激振动响应的经验性模型十分有限。Facchinetti 等[6]采用尾流振子模型对串列排列的双圆柱涡激振动进行描述,得到的计算结果能够在定性和定量上与实验和数值模拟结果保持一致。
本文主要研究二维并列双圆柱的涡激振动,同时建立一个能够预测结构涡激振动响应的经验性模型:由于特定间距比条件下的旋涡脱落频率出现分支,因此假设用两个具有不同固有频率(即斯特劳哈尔频率)的尾流振子来描述流体对结构的非线性动力作用,同时两个流体振子均满足van der Pol 方程,进而得到了结构振子和流体振子的耦合方程组,联立组成并列双圆柱涡激振动的尾流振子模型。采用实例基本数据,对经验性模型进行了数值求解,并与实验测量值进行对比分析,结果表明模型预报的响应能够很好地预计并列双圆柱涡激振动的结构振动特性和一般规律。
1 并列圆柱尾流振子模型
1.1 结构振动方程

图1 横向并列圆柱布置Fig.1 A schematic layout of two side-by-side cylinders in a cross-flow
二维并列双圆柱系统的布置如图1 所示。两个圆柱的直径均为D,圆心之间的间距为T,同时考虑在流速为U∞的均匀来流作用下,圆柱沿垂直流向的横向(Y 轴)运动。Facchinetti 等[7]给出了孤立弹性支承刚性圆柱的结构振动方程,对其进行拓展可以得到双圆柱系统的结构振动方程为:

式中:m=(ms+ma),ms为结构的质量,ma为流体的附加质量表示无粘流体的惯性作用力;ma=CaπD2ρ/4,Ca为流体的附加质量系数;r =(rs+rf),为结构粘性阻尼;rf为流体附加阻尼,表示流体的粘性作用力;k 为结构的刚度;Y1和Y2分别表示圆柱1 和圆柱2 的横向位置坐标,分别为结构横向运动速度和加速度;FVY1和FVY2分别表示脱落的旋涡对圆柱1 和圆柱2 的脉动升力,通常将升力定义为无量纲的升力系数形式,即FVY1=ρU2DCL1/2 和FVY2=ρU2DCL2/2。
1.2 尾流振子方程
尾流振子方程将结构近壁的尾涡动力特性通过非线性振子来模拟,例如采用van der Pol 方程或者Rayleigh 方程来描述其自激自限的谐振动过程,并与结构振子联立构成方程组,共同预测流固耦合系统的响应。Bishop 和Hassan[8]首先提出采用一个非线性自激的振子来表示作用在圆柱体上的升力。Hartlen 和Currie[9]以升力系数作为van der Pol 方程的状态变量,给出了尾流振子方程的数学表达式。国内外诸多学者补充并推广该方法,主要应用于研究孤立圆柱体,海洋立管和管道的涡激振动,如郭海燕[10]。
根据尾流振子模型建立的基本方法,引入无量纲参数q =2CL/CL0(其中的CL0为参考脉动升力系数[6])为尾流振子方程变量,同时满足受强迫激励的van der Pol 方程,其中强迫项表示结构对流体振子的耦合作用。与单圆柱情况不同,并列圆柱的间距比对斯特劳哈尔数可能存在影响,图2 给出了斯特劳哈尔数随间距比变化的函数关系,可以看到尾涡模态为偏向流动情况下,可能存在两个不同的主斯特劳哈尔频率。因此,假设在特定的T/D 范围内,流场中存在两个具有不同固有频率的尾流振子,其表达为:
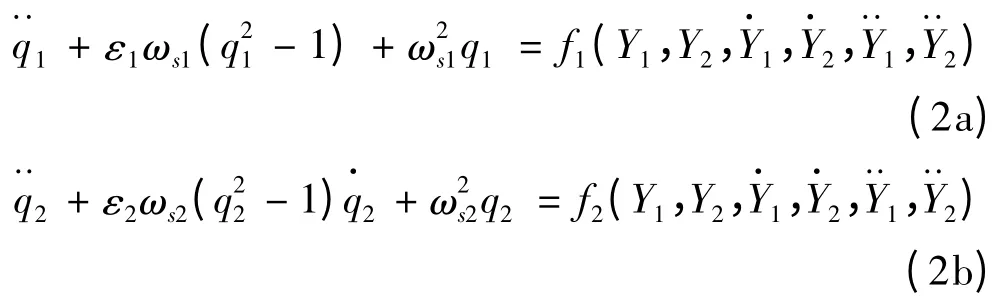
式中:ε 为van der Pol 方程参数;q1和q2分别表示圆柱1 和圆柱2 的尾流振子变量;ωs1和ωs2分别为圆柱1和圆柱2 相对应的旋涡脱落频率,同时也是流体振子的固有频率,其与斯特劳哈尔数的关系表达为ωs1,2=分别为耦合项。
Facchinetti 等[7]充分研究了单圆柱情况下结构与流体振子的耦合作用,分别对位移、速度、加速度三种耦合形式进行了对比和讨论。研究表明强迫项采用结构的加速度形式最为理想,能够反映共振特性,因此本文中采用的形式写为:
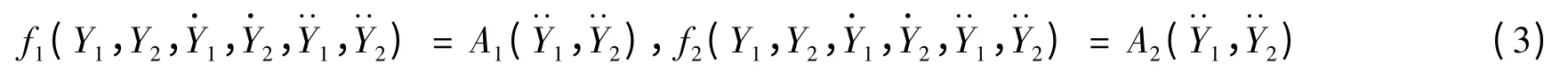
其中:A1和A2为实验参数。
因此,脉动升力系数可以表示为:

其中:(α1,β1,α2,β2)为模型的经验性参数,分别是间距比T/D 的函数并满足:

1.3 耦合振子模型
通过对结构振子方程式(1a)和式(1b)以及尾流振子方程式(2a)和式(2b)进行无量纲化,同时分别引入无量纲时间τ=(k/m)1/2t 和无量纲坐标y =Y/D,最终得到横向并列双圆柱的衰减阶(Reduced-Order)耦合振子模型为:
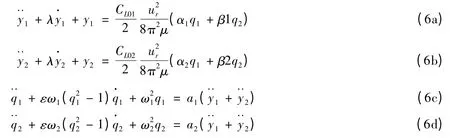
其中:此处的导数理解为对无量纲时间τ 求导;(α1,β1,α2,β2,a1,a2)为引入的无量纲参数;λ =r/(mk)为总阻尼比;ωn= (k/m)0.5为结构的固有频率;μ = m/ρD2为质量比;ur= U/fnD 为来流的约化速度;ω1,2=ωs1,2/ωn为频率比。
模型中的部分参数可以借鉴Facchinetti 等[7]尾流振子模型参数确定,本文中取a1=6,a2=6,ε =0.3。尾流振子方程中的频率ω1和ω2分别代表旋涡的脱落频率,需要根据不同尾涡模态中St随间距比的变化规律来确定。参考脉动升力系数CL01和CL02一般是在固定圆柱条件下测得的,通常与雷诺数Re 有关。模型的经验性参数(α1,β1,α2,β2)需要根据已有大量实验数据通过曲线拟合或最小二乘法确定其函数变化规律,由于现阶段可用的实验数据有限,因此这些参数在具体实验中给出。
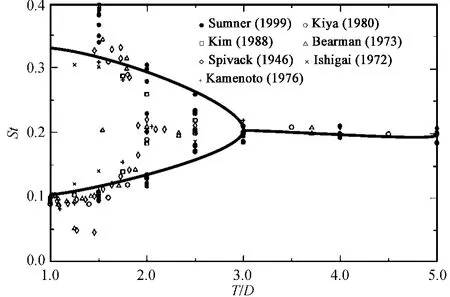
图2 斯特劳哈尔数与间距比T/D 的关系Fig.2 Strouhal number data as a function of transverse pitch ratio T/D
2 计算实例与结果分析
2.1 实例基本数据
文中对比分析的数据来源于Liu 等[11]中高质量比并列双圆柱的数值模拟实验结果和低质量比的并列排列双圆柱的模型实验测量结果。
Liu 等对不同间距比条件下的并列双圆柱进行了有限元CFD 数值模拟。分析中选取了三组不同的间距比,分别为T/D=1.8、3.0 和1.1。前两种工况的设计参数为:无量纲质量比m*=4ms/(ρπD2)=10,质量阻尼比m*ξ=0.3。而在工况T/D=1.1 条件下,两圆柱之间的距离很小,为了避免圆柱相撞需要调整结构的质量,其相应的设计参数取为无量纲质量比为m*=66,质量阻尼比为m*ξ =2.0。约化速度均控制在ur=5.0,相应的雷诺数为Re=200。
低质量比并列双圆柱的模型试验在船模拖曳水池开展。船模拖曳水池长108 m,池宽7 m,水深3.5 m。拖车车速0 ~6.5 m/s,拖车测量桥在垂直方向上的可调行程为0.4 m。实验中使用的管模型为圆柱体,采用的材料为硬聚氯乙烯(UPVC),直径10 cm,壁厚5 mm,管长1.0 m,管底部有配重,两端用水密封头密封。模型的辅助设备包括与拖车固定的框架结构和与圆柱管相连的可摆动连杆架结构组成,图3 给出了实验模型的装置图和三维仿真模拟图。实验的相应设计参数包括,无量纲质量比m*=1.4,质量阻尼比m*ξ =0.047 6。约化速度的范围在ur=4.2 ~16.8,相应的雷诺数范围为Re=2 ×104~8 ×104。

图3 并列双圆柱实验模型和实验三维仿真模拟Fig.3 The experimental model for two side-by-side cylinders and 3-D simulation
2.2 模型的数值求解
并列双圆柱的尾流振子模型即式(6a)~(6d)的数值求解使用的是自适应步长的四阶龙格-库塔方法。为了得到无量纲振幅与约化速度的关系,分别对增加流速和减小流速两种情况进行计算,其流速增量的大小取为0.01,同时需要满足后一流速条件下的初始条件取为前一流速的最终结果。时域模拟的时间控制为至少50 个振动周期,取稳定后的结果进行傅里叶分析从而得到振动的幅值与频率。
Liu 等[11]首先对不同间距比条件下的固定并列双圆柱进行了数值模拟实验,实验中可以测得参考脉动升力系数(CL0)和旋涡脱落频率,为本模型中经验性参数的确定提供参考。图4(a)和4(b)分别给出了参考升力系数和模型中的经验性参数随间距比的变化规律。
在T/D=3.0 工况下,Liu 等得到了弹性并列双圆柱的横向位移(Y/D)响应随时间的变化,如图5(a)。结果显示,两个圆柱的位移响应均为一般的简谐运动曲线,而且两者之间的振动互为反相位。根据已确定的模型参数,对本文模型的方程组(6a)~(6d)进行数值求解,图5(b)给出了经验模型的预报结果,两个圆柱的位移响应均为简谐曲线,而且相位相差半个周期,即互为反相位。对比Liu 等[11]的实验值,可以看到经验模型预测的振动频率与其吻合很好,但振动幅值偏小。

图4 参考升力系数和经验性参数随间距比的变化规律Fig.4 The reference lift coefficients and the empirical parameters versus spacing ratios
在T/D=1.8 条件下,相应的尾涡形为偏向流模式(biased flow pattern)。Liu 等的实验得到的升力和阻力时序曲线表现为强烈的不规则性,他们将产生的原因归结于尾涡的相互作用,而非转换性质(transition behavior)。同时,实验中监测出升力CL 谱存在两个主脱落频率。图5(c)给出了Liu 数值实验得到的圆柱位移响应,可以看到响应曲线表现为不规则性。与此不同,经验模型预报的圆柱振动中存在“拍”,即表明流体振子的一个频率与结构的固有频率相接近,如图5(d)所示。因此,实验中表现的强不规则性可能还包含了流-固之间的耦合作用。
当间距比取为T/D =1.1 时,两个圆柱之间的距离很近,通常圆柱的位移幅值随质量比的增加而减小,因此选用大质量比来保证两圆柱不会发生碰撞。Liu 等设m*=66,并给出了圆柱的位移响应曲线,如图5(e)。从圆柱剪切层脱落的发展旋涡存在很强的相互作用,同时还受到间隙流的影响,导致位移响应中有另一个额外峰值,位移谱也显示出存在两个主频率。图5(f)给出了经验模型的预报结果,其得到的振动频率和幅值都与实验结果一致。
2.3 低质量比响应分析
低质量比并列双圆柱涡激振动的模型实验分别对T/D=4.7,4.2,3.9,3.5,3.0 和2.6 共六种工况进行了研究和讨论。图6(a)和6(b)给出了在间距比T/D=2.6,约化速度ur=6.3 条件下圆柱1 和圆柱2 借助加速度传感器得到的结构顶部横向位移加速度结果,由于提取的信号中存在高频噪声,需要对其进行光顺滤波处理,本文采用低通与高通滤波方式对原始数据进行处理[12]。滤波后的加速度结果通过数值积分可以得到横向位移随时间的变化曲线,如图6(c)和6(d)所示。经过谱分析从而得到了响应的振幅和频率,如图6(e),以及斯特劳哈尔数随间距比的变化关系,如图6(f)所示。
低质量比涡激振动的显著特点是圆柱的位移响应幅值相对较大,因此有必要对圆柱体横向无量纲最大振幅(Y/D)进行讨论。数值求解经验模型的方程组,式(6a)~(6d),其中参考升力系数取为经验值CL01=CL02=0.3,模型的其它经验性参数的取值及其随间距比的变化规律在图6(g)中给出,对比中高质量比的经验性参数(图4),可以看到两者的变化趋势相近。
图6(h)给出了T/D=4.7 和单圆柱条件下,模型实验得到的圆柱最大振幅与约化速度的变化关系。可以看到并列双圆柱的振幅响应及峰值位置与单圆柱的测量结果接近,因此可以认为两个圆柱之间的距离较远,相互之间的影响较小。经验模型的预报结果与实验结果的趋势一致,振幅峰值都出现在约化速度ur=6.3附近,随后最大振幅逐渐减小,但是预测的峰值数值偏小。
图6(i)给出了T/D=2.6 条件下,模型实验得到的圆柱最大振幅与约化速度的关系。实验中发现圆柱的振幅响应在随约化速度变化的过程中出现了两个峰值,分别是在约化速度ur=6.3 和12.6 附近,其产生的原因可能是由于该间距比条件下结构所受的流体力存在两个主频率,随着流速的增加两个主频率分别激起结构的共振从而出现两个峰值。经验模型也预报出两个振动峰值,出现的位置和数值均小于实验的观测结果,但是最大振幅随约化速度的变化趋势与实验结果基本一致。

图5 不同间距比条件下数值模拟和经验性模型得到的Y/D 随时间的变化Fig.5 Y/D time series for numerical simulation and empirical model under different spacing ratios
3 结 语
本文主要针对并列双圆柱的涡激振动,建立了一种新的尾流振子模型,用来预测结构的涡激振动响应。现阶段的研究表明,在特定间距比条件下,旋涡的脱落频率(或斯特劳哈尔频率)出现分支,即可能存在两个主脱落频率。因此,本文提出以两个具有不同固有频率的尾流振子来共同描述结构的近壁尾涡动力特性,同时两个流体振子均满足van der Pol 方程,进一步推导出结构振子和流体振子耦合的方程组,用来模拟并列双圆柱的流固耦合现象。
本文同时给出了经验模型的数值求解方法,并结合Liu 等[11]的中高质量比数值模拟实验和低质量比模型实验提供的设计数据,对该经验模型进行了数值计算,得到的预测结果与实验结果进行了对比。分析结果表明,预测的结构位移响应和最大振动幅值等变化规律与相应的实验结果趋势一致,能够反映并列双圆柱涡激振动的结构振动特性和一般规律。
[1]Zdravkovich M M.The effects of interference between circular cylinders in cross flow[J].Journal of Fluids and Structures.1987,1(2):239-261.
[2]姚熊亮,陈起富.均匀流场中并列圆柱涡激振动的现状与预测[J].海洋工程,1995,13(3):37-47.
[3]Williamson C H K.Evolution of a single wake behind a pair of bluff bodies[J].Journal of Fluid Mechanics.1985,159:1-18.
[4]Sumner D,Wong S S T,Price S J,et al.Fluid behavior of side-by-side circular cylinders in steady cross-flow[J].Journal of Fluids and Structures.1999,13:309-338.
[5]Wang Z J,Zhou Y,Li H.Flow-visualization of a two side-by-side cylinder wake[J].Journal of Flow Visualization & Image Processing,2001,9:123-138.
[6]Facchinetti M L,Langre E,Fontaine E,et al.VIV of two cylinders in tandem arrangement:analytical and numerical modeling[C]∥Proc. of the 12th (2002)International Offshore and Polar Engineering Conference.2002:524-531.
[7]Facchinetti M L,Langre E,Biolley F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19:123-140.
[8]Bishop R E D,Hassan A Y.The lift and drag forces on a circular cylinder in a flowing fluid[C]∥Proc.of Royal Society Series A,1963,277:32-50.
[9]Hartlen R T,Currie I G.Lift-oscillator model of vortex-induced vibration[J].Journal of the Engineering Mechanics,1970,96:577-591.
[10]Li Xiao-min,Guo Hai-yan,Meng Fan-shun.Nonlinear coupled in-line and cross-flow vortex-induced vibration analysis of top tensioned riser[J].China Ocean Engineering,2010,24(4):749-758.
[11]Liu Y,So R M C,Lau Y L,et al.Numberical studies of two side-by-side elastic cylinders in a cross-flow[J].Journal of Fluids and Structures.2001,15:1009-1030.
[12]张建侨,宋吉宁,吕林,等.柔性立管涡激振动实验的数据分析[J].中国海洋平台,2009,24(4):26-32.

