自动焦度计定量计算式的研究

谢银月， 李湘宁

（1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海医疗器械高等专科学校 基础教学部，上海 200093）

顶焦度（vertex power）是眼镜镜片最重要的光学参数.对常见的眼镜镜片而言，后焦距的倒数就是眼镜镜片的顶焦度［1］.顶焦度的单位名称为屈光度，单位符号为D.在不同文献资料中，关于眼镜镜片的术语和参数名称不尽相同，本文的相关表述主要依据现行使用的《中华人民共和国国家计量检定规程》（焦度计）JJG 580－2005 和《中华人民共和国国家标准》（眼镜镜片，第1部分：单光和多焦点镜片眼镜镜片）GB10810.1－2005.

焦度计是眼镜行业最重要的计量仪器，主要用于测量眼镜镜片的球镜顶焦度、柱镜顶焦度和柱镜轴位等.自动焦度计问世时间不长，国外产品占据大部分市场份额［2］.自主研制自动焦度计的一个关键内容是对光学系统测量原理的充分理解.作者查阅了大量文献资料，并没有查阅到关键的定量计算式，还发现，有些文献对测量原理的分析不够细致，甚至出现错误，这不利于自主研制自动焦度计.作者对带孔光阑为4个小孔的光学系统测量原理进行深入研究，用棱镜效应理论推导出被测镜片的球镜顶焦度、柱镜顶焦度和柱镜轴位的计算式，并用Zemax软件仿真测量，证明了这个计算式的可靠性.

1 光学系统

图1是测量镜片顶焦度的光学系统示意图，u为带孔光阑到观察屏的距离，F′为后焦点.点光源位于准直物镜的物方焦点上，经准直物镜后发出平行光，平行光线经被测镜片后发生偏折，再经过光阑到达观察屏［3］.

图1 测量镜片顶焦度的光学系统示意图Fig.1 Optical system for measurement of ophthalmic lenses’vertex power

带孔光阑上有4个小孔，小孔位置如图2所示，各小孔 坐 标 为A（0，h），B（0，－h），C（－h，0），D（h，0）.对特定系统而言，小孔在观察屏上的落点位置与被测镜片的顶焦度之间存在确定的函数关系，光学系统测量原理的关键内容是建立这个函数关系式.对球镜镜片而言，上述函数关系式很易推出，但若被测镜片是散光镜片，则情况比较复杂.

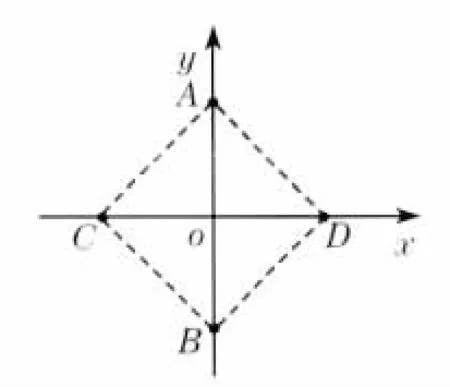
图2 光阑上4个小孔的分布图Fig.2 Positions of four holes on diaphragm

散光镜片可等效为球镜镜片和柱镜镜片的叠加［4］，表示为“FSDS／FCDC×θ”，其中，FS，FC和θ分别代表该散光镜片的球镜顶焦度、柱镜顶焦度和柱镜轴位.测量散光镜片应包含FS，FC和θ这3个特征量的测量.球镜镜片是柱镜顶焦度为零的特殊的散光镜片.

2 眼镜镜片的棱镜效应与棱镜度

光线经过棱镜后，总是向棱镜底的方向偏折，这称为棱镜效应.棱镜度用于定量描述棱镜效应，数值上等于光线通过镜片后，在每米距离上由偏折面产生的位移厘米数.眼镜镜片可看作是无数个小棱镜的叠加，因此也存在棱镜效应，镜片上某点对光的偏折力用该点的棱镜度来表示［5］.

由图3可分析出，镜片上任意一点G 的棱镜度P 与镜片顶焦度F′之间的关系满足

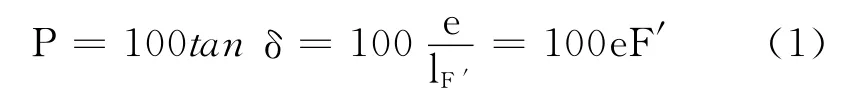
式中，δ为光线偏折角；lF′为后焦距；对球镜镜片而言，e是G 点到光心的距离；而对柱镜镜片而言，e是G 点到柱镜轴的垂直距离.

图3 眼镜镜片的棱镜度Fig.3 Prismatic power of ophthalmic lens

设G 点坐标为G （x，y），如图4 所示，镜片在xoz子午面与yoz 子午面（图4中z轴没有画出）上的顶焦度为［6］

图4 被测镜片上的光线入射点Fig.4 Incident light spot on the ophthalmic lens under test

特别应该指出，如果根据式（1）、式（2）得出，G点的棱镜度在x，y 轴两个方向上的分量为那是错误的，即式（3）是不正确的，在有些文献中就出现了这样的错误.因为对球镜镜片和柱镜镜片而言，式（1）中的距离e含义不同，故应把球镜与柱镜分开考虑，单独得出球镜棱镜度和柱镜棱镜度，然后两者相加［7］.设G 点到柱镜轴的垂直距离为e，当θ≤90°时，有

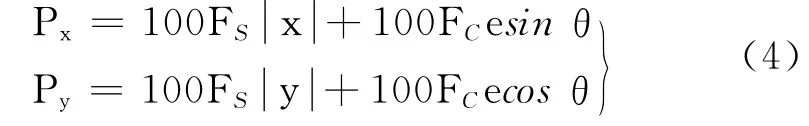
若是θ＞90°，则式（4）中cosθ应用cos（180°–θ）代替.

3 推导眼镜镜片光学参数的计算式

图1中，设带孔光阑与观察屏之间的距离为u，被测镜片后表面与光阑之间的距离远小于u，可近似为零.根据镜片的棱镜效应与小孔对称性，可以分析出观察屏上的4个落点A′，B′，C′，D′的移动规律及它们的分布特点：球镜顶焦度FS使落点对称收缩或扩张到a，b，c，d 点；当FC为正时，4个落点再垂直移向柱镜轴；当FC为负时，4个落点再垂直远离柱镜轴；并且A 与A′之间的距离等于B 与B′之间的距离，C 与C′之间的距离等于D 与D′之间的距离，A′与B′、C′与D′分别关于原点对称，如图5所示.

图5 观察屏上4个落点的位置Fig.5 Positions of four light spots on observation screen

设相对于初始位置（不放被测镜片时的光斑位置），落点A′在x轴、y轴方向的偏移量为x1，y1，落点D′的偏移量为x2，y2，规定朝x轴、y轴正方向偏移时，偏移量为正，反之为负.根据落点分布的对称性特点，无论FC为正或者为负，图5（a）和图5（b）的落点A′，B′，C′，D′的坐标都可以写成A′（Δx1，h＋Δy1），B′（－Δx1，－h－Δy1），C′（－h －Δx2，－Δy2），D′（h＋Δx2，Δy2）.由式（4），无论θ≤90°或者θ＞90°，与小孔对应的被测镜片上4个点的棱镜度都可写成

根据式（1）和偏移量的正负分析，无论FC为正或者为负，无论θ≤90°或者θ＞90°，都满足

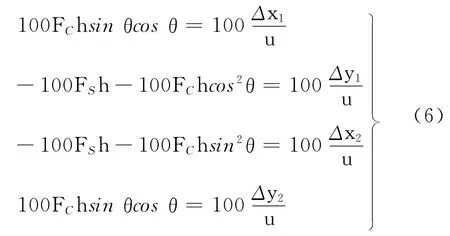
从而得到落点A′，D′在x 轴、y 轴的偏移量与FS，FC和θ 的函数关系

若实际探测到的是观察屏上落点的坐标值，由于存在对称性，只需探测A′，D′的坐标，即A′（x1，y1），D′（x2，y2），理论上y2＝x1.这样，Δx1＝x1，Δy1＝y1－h，Δx2＝x2－h，求解方程组（7），可得到FS，FC和θ 的计算式

当柱镜顶焦度FC为正时，式（8）中第一式的“∓”取负，反之取正；而第三式的“±”与FC相同.因此，只要探测到x1，y1和x2的值，就可计算得到被测镜片的球镜顶焦度FS、柱镜顶焦度FC、柱镜轴位θ.

应该特别强调，式（8）有一个适用条件，那就是图1中被测镜片的光学中心应位于光学系统的光轴上，这是光阑设计为4个对称小孔（而不是2个小孔）的重要原因.此外，若另探测到B′，C′的坐标值，则也可以利用式（8）进行计算，然后取平均值以提高测量精度.

4 Zemax仿真测量

Zemax是目前广泛应用的光学设计软件［8］，用它可方便设计出正、负2个散光镜片.在面型中选择“Paraxial XY”，选X，Y 方 向 的 光 焦 度 分 别 为＋6.000D和＋2.000D，这等效于一个正散光镜片（FS＝＋2.000D，FC＝＋4.000D，θ＝90°）；选X，Y方向的光焦度分别为－8.000D 和－2.000D，这等效于 一个 负 散 光 镜 片（FS＝－2.000 D，FC＝－6.000D，θ＝90°）.

带孔光阑用透镜阵列进行仿真模拟，考虑到设置2×2透镜阵列不能满足如图2所示的4个小孔的分布特点，因此设置3×3 透镜阵列，模拟出9个“小孔”，选择符合位置要求的4个“小孔”A，B，C，D 作为关注对象，形成4个小孔的仿真光阑，每个透镜单元的尺寸为3×3，单位为mm，波长选用0.632 8μm.

按图1所示的光学系统进行结构设计，不放入镜片时的像面点列图就是仿真带孔光阑，如图6（a）所示.分别放入正、负散光镜片后，像面点列图发生明显变化，如图6（b）和图6（c）所示.需要测量的是像面点列图中相关光斑的中心位置坐标值（x，y），这在Zemax中可方便实现.如果不是仿真测量，而是实际仪器的测量，则可利用图像处理软件得到每个光斑中心的坐标值［9－10］.

图6 仿真测量眼镜镜片的像面点列图Fig.6 Spot diagram on image surface in simulation measurement of astigmatic－power lens

仿真带孔光阑与像面的距离u＝70.000 mm，测得仿真光阑的4个小孔的平均坐标值h＝2.962 1mm，正 散 光 镜 片 的 A′，D′ 坐 标 为A′（－0.000 3，2.547 1），D′（1.739 0，0.001 6），由式（8）计算得到FS＝＋2.001 D，FC＝＋3.897 D，θ＝90.02°，FS和FC的百分误差分别为0.05%和2.58%.负散光镜片的A′，D′坐标为A′（0.000 1，3.386 3），D′（4.597 6，0.000 4），由式（8）计算得到镜片的FS＝－2.046 D，FC＝–5.842 D，θ＝90.00°，FS和FC的百分误差分别为2.30%和2.63%.测量值与理论值基本相符，点列图中光斑中心位置的确定存在偏差，这是仿真测量的误差主要来源.

5 结束语

本文推导出被测镜片的球镜顶焦度FS、柱镜顶焦度FC和柱镜轴位θ 的具体计算式，并用Zemax软件进行仿真测量，证明了这个计算式的可靠性.

在实际设计光学系统时，光阑上的小孔需要有一定的孔径，小孔在观察屏上的落点实际是光斑，式（8）中的落点坐标值实际是光斑中心位置的坐标值.光学系统与图像处理系统相结合，即可实现眼镜镜片光学参数的自动测量.

［1］刘晨.焦度计综述［J］.应用光学，2004，25（1）：55－57.

［2］廖海洋，杨并上.一种数字投影式顶焦度测量仪［J］.光电工程，2005，32（2）：52－55.

［3］刘晨，张辉，柯玉军.自动焦度计的研制［J］.光学仪器，2003，25（6）：39－44.

［4］秦琳玲，余景池.哈特曼法检测渐进多焦点镜片［J］.光学与光电技术，2008，6（5）：84－87.

［5］孟建国.视光学——眼镜光学［M］.上海：东华大学出版社，2004.

［6］王静.棱镜眼镜棱镜度和棱镜基底取向检测方法的探讨［J］.计量与测试技术，2009，36（5）：28－29.

［7］瞿佳，王勤美，高潮.眼镜学［M］.北京：中国标准出版社，1993.

［8］徐欢，李湘宁，周果.基于Zemax 软件的大齿距等厚菲涅尔透镜的设计［J］.上海理工大学学报，2007，29（1）：99－102.

［9］Salas－Peimbert D P，Trujillo－Schiaffino G，Gonzá1ez－Silva J A，et al.Simple Hartmann test data interpretation for ophthalmic lenses［J］.Review of Scientific Instruments，2006，77 （4）：0431021－0431025.

［10］周果，李湘宁，徐欢.基于摄像头采集和图像处理的机织物密度检测［J］.上海理工大学学报，2007，29（2）：171－174.