定、转子极弧可变时无轴承开关磁阻电动机的数学模型

陈小元

(1．丽水学院，浙江丽水323000;2．浙江方正电机股份有限公司，浙江丽水323000)

0 引 言

无轴承开关磁阻电动机(以下简称BSRM)是利用磁悬浮轴承与普通开关磁阻电动机(以下简称SRM)两者定子结构的相似性，在普通SRM 定子齿上增加一套悬浮绕组用于产生悬浮力，根据电机转子径向位移，通过实时调节该悬浮绕组电流改变电机气隙磁场的分布产生相应的径向悬浮力，使得电机转子径向稳定悬浮，最终同时实现电机转子的旋转和 自 悬 浮 控 制［1－12］。BSRM 不 仅 可 充 分 发 挥SRM 控制灵活、容错能力强和高速适应性强等优点，而且具有磁悬浮电机无摩擦、无润滑和长寿命等优良特性，在航空航天及超洁净等驱动领域具有潜在的应用前景。

精确的数学模型是保证BSRM 高速旋转并稳定悬浮的理论基础。目前三相12 /8 结构BSRM 的数学模型推导主要采用虚位移法［4－9］和Maxwell 张量法［10－12］，其中虚位移法通过气隙磁导分割方法求得电机绕组的电感矩阵进而得到电感的磁场储能，转矩与悬浮力表达式由对磁场储能求偏导得到。

在12 /8 结构的BSRM 现有数学模型的推导时，定、转子极弧角均为15°，且由于电机径向气隙长度相对较小，可认为定子和转子的齿宽相等［5－12］。此时定子极弧角与转子机械位置角θ 绝对值之差即为定子齿与转子齿重叠部分所占极弧度数，定子齿和转子齿重叠部分气隙磁导P1，边缘气隙磁导P2和P3均为转子位置角θ 的函数，方便积分求解，从而确保电感、转矩及悬浮力等电磁参数表达式为BSRM 结构参数的单值函数。

BSRM 实际应用中，满足径向悬浮力和转矩的输出要求是定、转子极弧选取的基本原则，这就需要在设计BSRM 时，根据不同应用场合，优化选取定、转子极弧。若定子齿与转子齿宽不相等，则定子齿和转子齿存在完全重叠区域。在此完全重叠区域内，P2和P3不再相等，P1亦为定值。此时现有BSRM 的数学模型将不能适用，需重新推导新的数学模型。因此，推导BSRM 在定、转子极弧参数可变时的数学模型具有重要意义。

本文分析了12 /8 结构的双绕组BSRM 定、转子极弧角的选取原则，计算了转矩和悬浮力随定、转子极弧的变化关系。基于BSRM 的虚位移模型的推导方法，提出了一种采用分段函数表示可适用于定、转子极弧不相等时的BSRM 新型数学模型，最后与传统数学模型以及采用FEM 计算的主绕组和悬浮绕组电感结果进行了比较。

1 定、转子极弧的选取

按照三相12 /8 结构的BSRM 相关研究文献习惯，把转子位置零度角位置定义在定转子齿与转子齿轴线重合位置，即绕组电感最大处［1－12］。BSRM通常采用单相交替工作控制策略，每相主绕组和悬浮绕组开通区间为15°机械角，即若A 相主绕组和悬浮绕组导通区间为－7．5°～7．5°范围转子位置角，则B 相和C 相分别与A 相相差15°和30°。

而对于普通SRM，为确保在顺时针和逆时针两个方向均可起动，定子极弧角βs和转子极弧角βr须满足［13－14］:

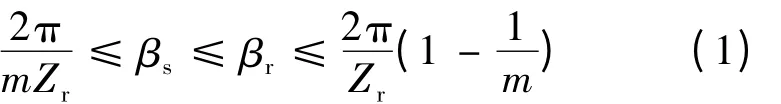
式中:m 为电机相数。由于BSRM 结构与SRM 的相似性，式(1)亦适用于BSRM。

气隙磁导磁路路径的选取及等效是基于等效磁路法推导BSRM 的数学模型过程中的关键。由于推导过程中设定由P1，P2和P3之和构成每个定子极下的总磁导，因此为确保相绕组导通区内任一位置间定子齿和转子齿之间有重叠，则βs和βr必须满足:

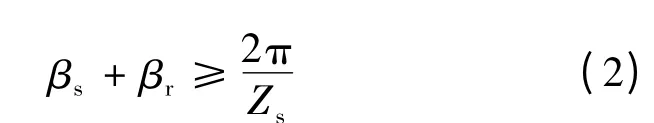
图1 为BSRM 的悬浮力及电磁转矩随βs和βr的变化关系。由图1(a)可知，当βs= 15°时，有效输出转矩宽度与幅值随βr的增大均变小;随βr递增，悬浮力亦增大，但最大悬浮力(发生在转子位置角θ=0 处)基本不变。由图1(b)可知，当βr与βs相等时，随着βr与βs增大，悬浮力随之增大，有效输出转矩宽度增加而幅值略有减小。

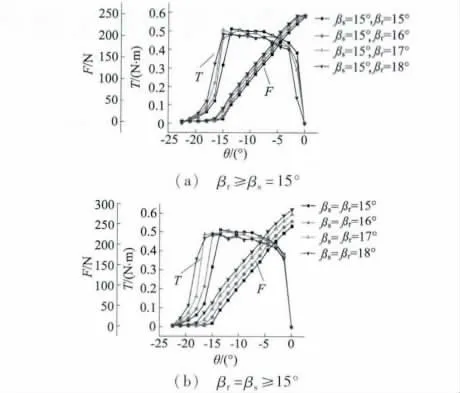
图1 BSRM 转矩、悬浮力与βs、βr 的关系

2 通用数学模型

2.1 磁导表达式

以转子极弧角大于定子极弧角的情况(即βr≥βs)，推导可适用于定、转子极弧不相等时的BSRM新型数学模型。

由于从θ = (βr－βs)/2 处即定、转子前齿尖重合位置到θ = 0 处即对齐位置的区间内，气隙磁导P1不变，所以BSRM 的数学模型可采用分段函数表示，即分别推导θ≥(βr－βs)/2 和θ ＜(βr－βr)/2 时的气隙磁导P1、P2和P3，进而得到对应的数学模型。图2(a)和图2(b)分别为两种情况下的气隙1处的磁路分割图。

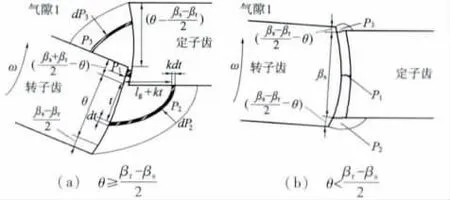
图2 两种情况下气隙1 的磁路分割图

根据文献［4－5］的BSRM 的磁导推导过程，可得磁导P2:

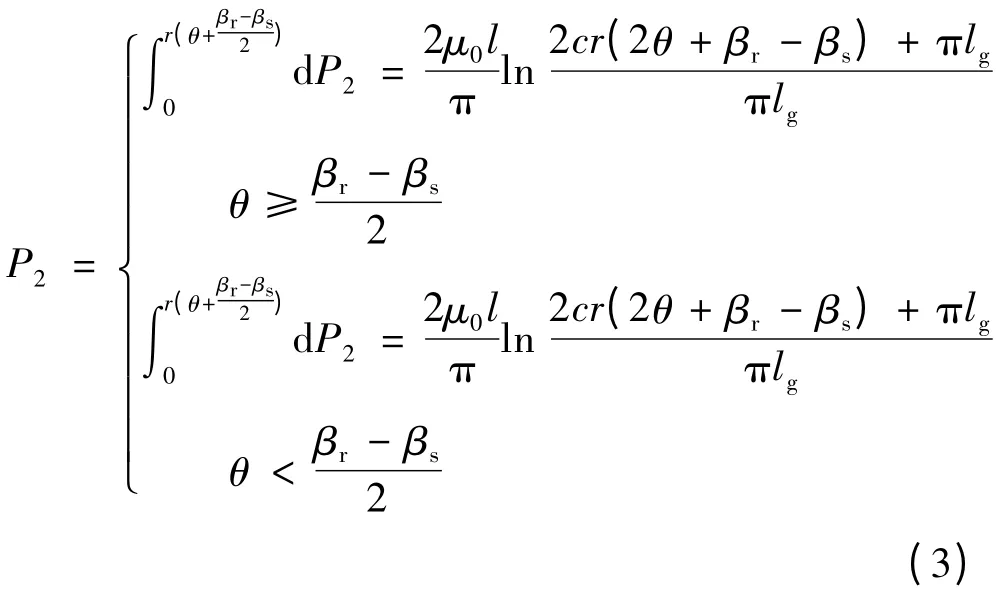
式中:θ 为位置角的绝对值;μ0为空气的磁导率;l 为电机轴向长度;lg为气隙平均长度;c 为常数，c =1. 49。

磁导P3:

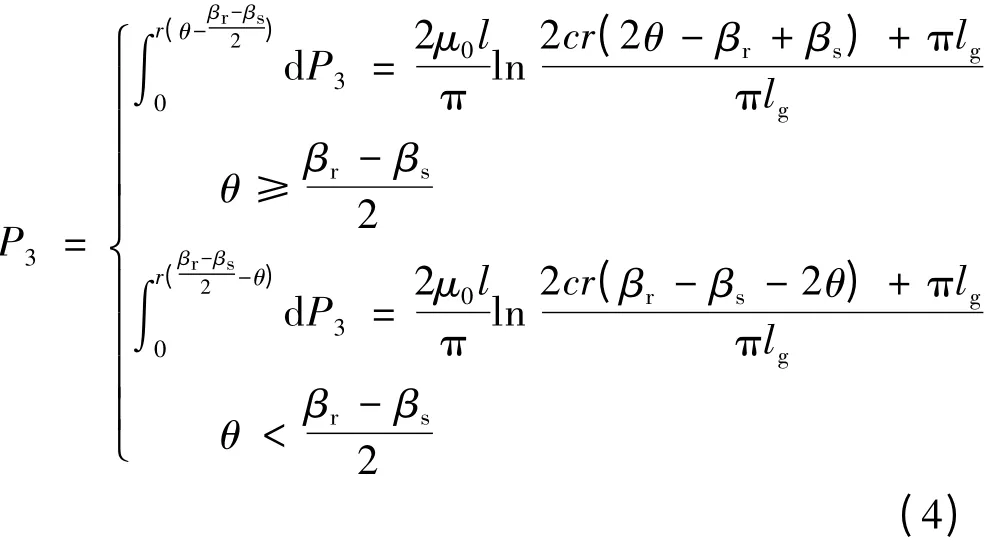
磁导P1:

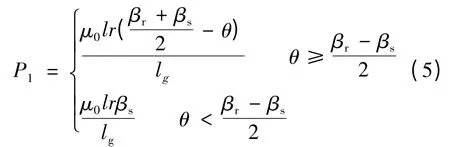
图2 的气隙1 处的磁导Pa1可通过三处磁导叠加得到:

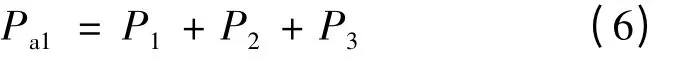
由式(3)～式(6)得一个齿极下的气隙总磁导Pa:

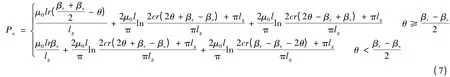
考虑转子径向α 轴和β 轴上的位移，用l0± α与l0± β 来替换式(7)中的气隙平均长度lg，其中l0为转子在中心位置时定、转子间气隙的长度，α 和β分别代表α 轴和β 轴上的径向位移量。因此，A 相4个齿极下的气隙磁导Pa1～Pa4分别为:

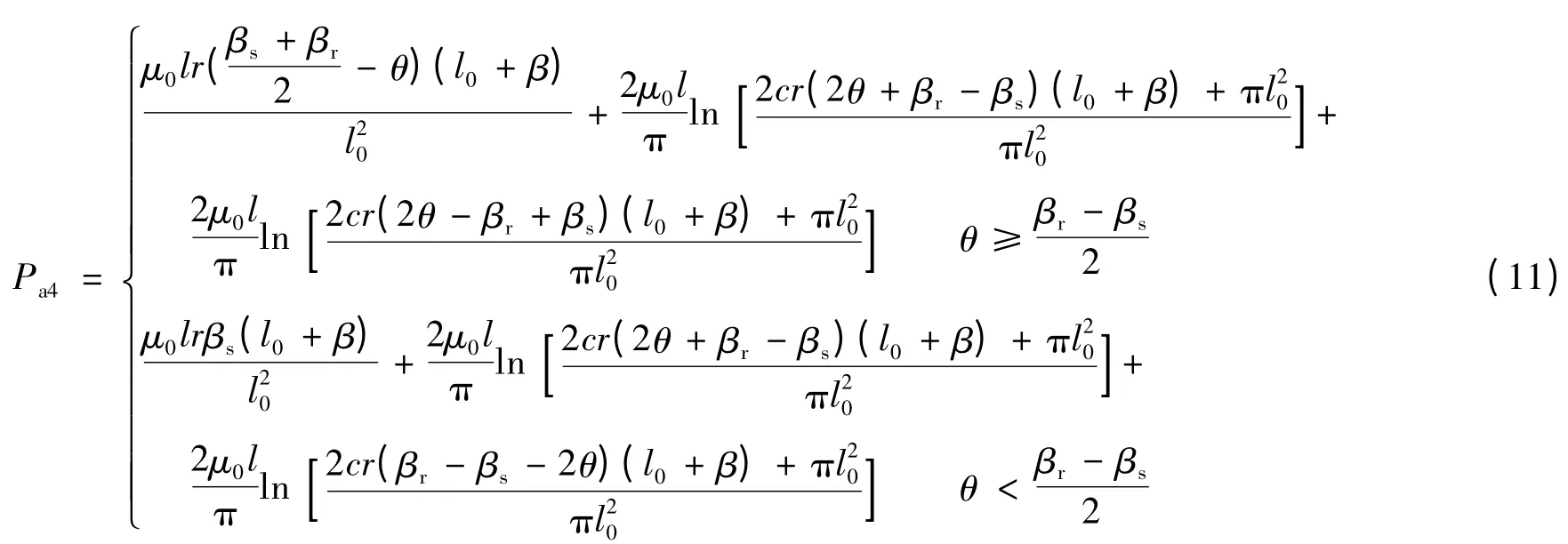
2.2 电感矩阵

把气隙磁导表达式(8)～式(11)代入文献［5］中式(1)，可分别得BSRM 的主绕组和悬浮绕组的自感及互感表达式。考虑到l0远大于转子径向位置偏移量α 和β，主绕组和悬浮绕组的自感及互感表达式中的径向位移α 和β 的高次项可忽略。即可分别得A 相主绕组的自感Lma，α 方向悬浮绕组的自感Lsa1和β 方向悬浮绕组的自感Lsa2，主绕组分别与α 方向悬浮绕组和β 方向悬浮绕组间的互感Msma1和Msma2，α 和β 方向悬浮绕组间的互感Msa12:

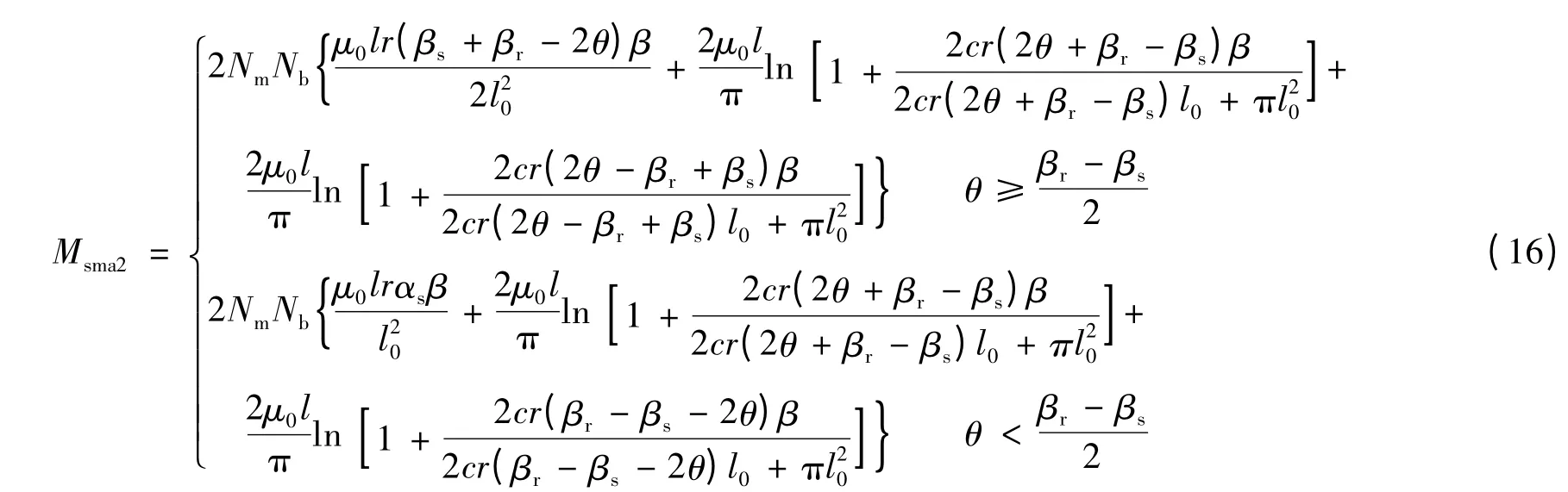
2.3 悬浮力表达式

把互感表达式(15)和式(16)代入文献［6］中式(22)和式(23)，可得作用在转子上的径向悬浮力Fα、Fβ悬浮力表达式分别为:

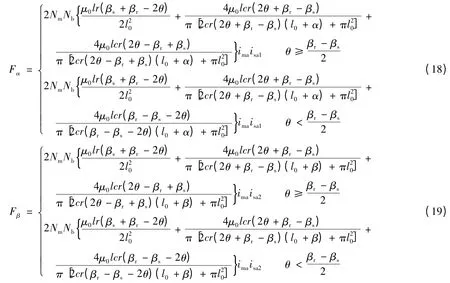
式(18)和式(19)方括号内的第2 项及第3 项在数值上远小于第1 项，即忽略第2 项及第3 项中的转子径向位移量对数学模型的精度影响不大。因此，可得悬浮力系数Kf(θ)为［5－6，9－10］:

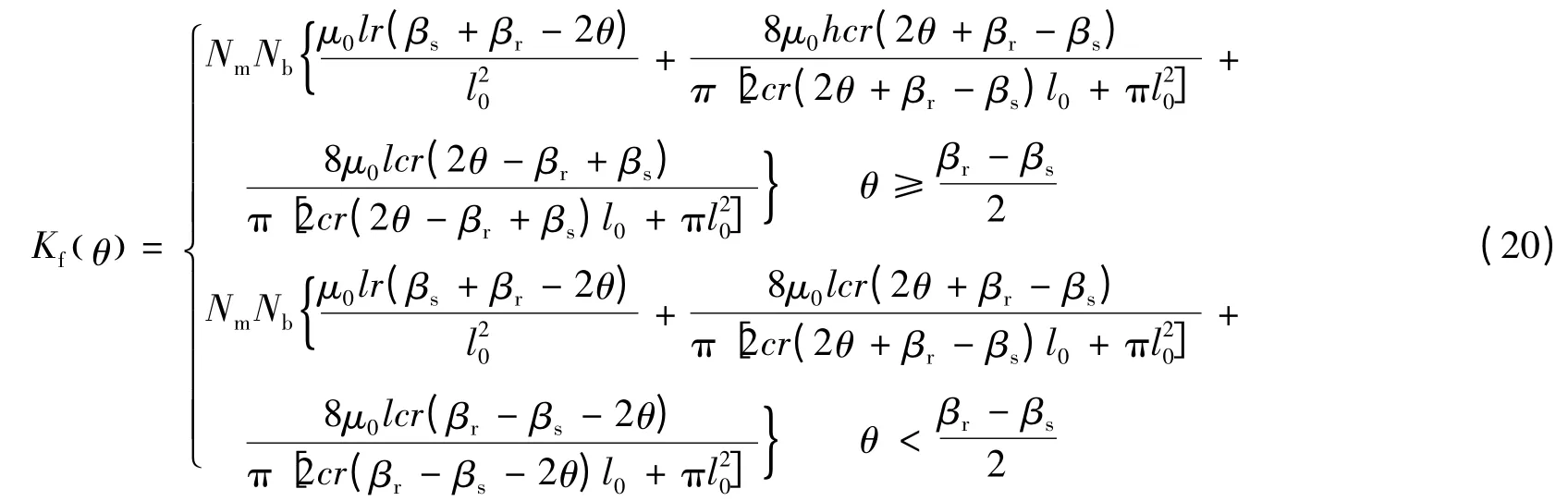
2.4 转矩表达式

A 相绕组导通时的瞬时电磁转矩:

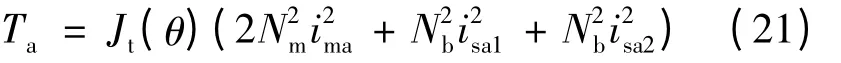
式中:Jt(θ)为转矩系数［5－6，9－10］，在电感上升和下降区间分别:

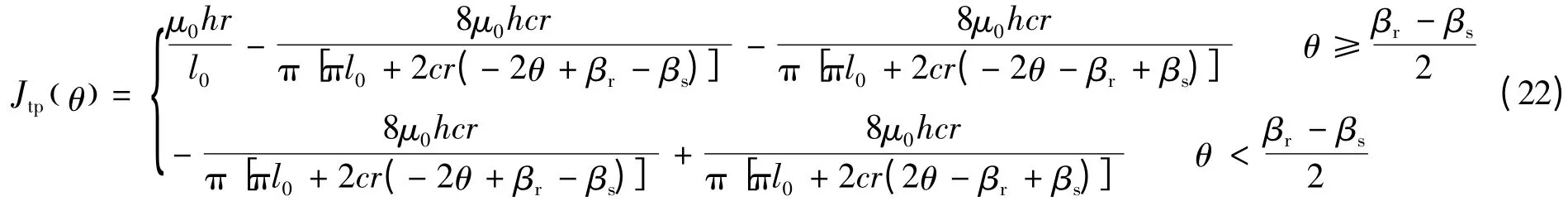
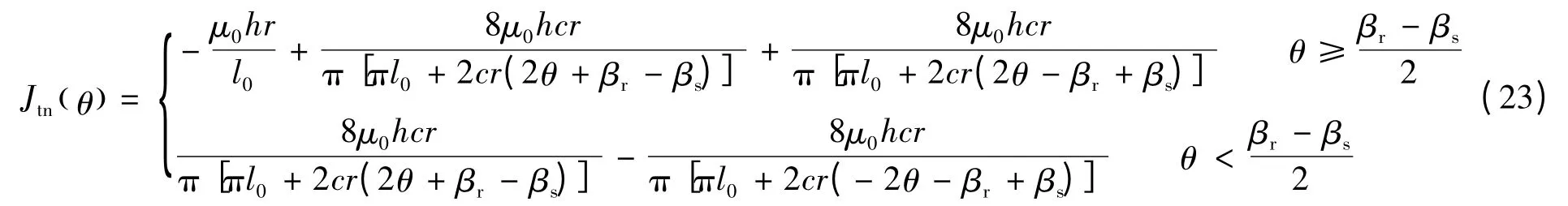
3 数学模型分析

由于本文的BSRM 新型数学模型的电感、转矩和悬浮力等参数的表达式中增加了定子极弧角βs与转子极弧角βr变量，因此该模型适用于定、转子极弧角不等的情况。

图3 为βs= 15°及βr= 17°时，新型数学模型、文献［4］中的原MM 及采用FEM 计算的主绕组和悬浮绕组电感计算结果。相对于文献［4］中的原数学模型，新型数学模型计算得到的主、悬浮绕组自感与FEM 计算的结果更为接近，表明了新型数学模型的准确性。

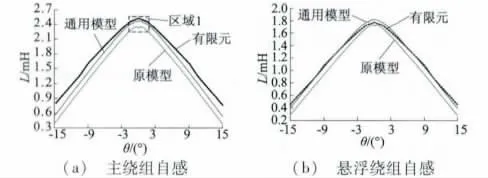
图3 绕组自感计算结果对比(βs = 15°、βr = 17°)

图3(a)中的主绕组自感区域1 的放大图如图4所示，BSRM 新型数学模型分别在转子位置角θ = －(βr－βs)/2 及(βr－βs)/2 处出现两个凹陷，而原数学模型的自感曲线在转子位置角θ = 0 处出现一个凹陷［5－6］。但计算结果表明新型数学模型的两个凹陷深度小于原MM 的凹陷深度，且过度相对圆滑。

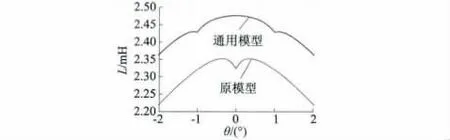
图4 主绕组自感区域1 的放大图

4 结 语

本文分析了12 /8 结构的双绕组BSRM 定、转子极弧角的选取原则，计算了转矩和悬浮力随定、转子极弧的变化关系。针对BSRM 的传统数学模型只适用于固定定、转子极弧的局限性，提出了一种适用于定、转子极弧可变的BSRM 的新型数学模型。基于BSRM 传统虚位移模型的推导方法，推导了利用分段函数表示的包括定、转子极弧两个变量的新型数学模型解析表达式，并将新型数学模型、传统数学模型以及FEM 计算的主绕组和悬浮绕组电感结果进行了比较。结果表明，新型数学模型的电感计算结果准确。且新型数学模型中的转矩和悬浮力方程包括定、转子极弧这两个变量，对定、转子极弧没有限制，拓宽了电机定、转子极弧的选取，为BSRM 的优化设计奠定了理论基础。

［1］ Takemoto M，Shimada K，Chiba A，et al．A design and characteristics of switched reluctance type bearingless motors［C］/ /Proceedinds of the 4th International Symposium on Magnetic Suspension Technology(NASA/CP－1998－207654)．NASA，1998:49－63．

［2］ Takemoto M，Suzuki H，Chiba A et al．Improved analysis of a bearingless switched motor［J］．IEEE Trans．on Industry Application，2001，37(1):26－34．

［3］ 杨钢，邓智泉，张媛，等．无轴承开关磁阻电机实验平台的设计与实现［J］．中国电机工程学报，2006，26(22):97－103．

［4］ Takemoto M，Chiba A，Akagi H et al．Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation［J］．IEEE Trans．on Industry Application，2004，40(1):103－112．

［5］ 邓智泉，杨钢，张媛，等．一种新型的无轴承开关磁阻电机数学模型［J］．中国电机工程学报，2005，25(9):139－146．

［6］ 曹鑫，邓智泉，杨钢，等．新型无轴承开关磁阻电机双相导通数学模型［J］．电工技术学报，2006，21(4):50－56．

［7］ 孙玉珅，吴建兵，项倩雯．基于有限元法的磁悬浮开关磁阻电机数学模型［J］．中国电机工程学报，2007，27(12):33－40．

［8］ 孙玉坤，刘羡飞，王德明，等．基于有限元分析的磁悬浮开关磁阻电机数学模型的全角度扩展［J］．电工技术学报，2007，22(9):34－39．

［9］ 刘泽远．无轴承开关磁阻电机的电磁基础研究［D］．南京:南京航空航天大学，2010．

［10］ 曹鑫，邓智泉，杨钢，等．无轴承开关磁阻电机麦克斯韦应力法数学模型［J］．中国电机工程学报，2009，29(3):78－83．

［11］ 曹鑫．12 /8 极无轴承开关磁阻电机的研究［D］．南京:南京航空航天大学，2010．

［12］ 杨艳，邓智泉，曹鑫，等．无轴承开关磁阻电机径向电磁力模型［J］．电机与控制学报，2009，13(3):377－382．

［13］ 陈昊．开关磁阻调速电动机的原理·设计·应用［M］．徐州:中国矿业大学出版社，2000:70－72．

［14］ 吴建华．开关磁阻电机设计与应用［M］．北京:机械工业出版社，2000:119－124．