考虑转子磁场谐波的永磁同步电动机仿真
刘仕钊,宋 琼,舒 杨,陈文颖
(中国工程物理研究院总体工程研究所,四川绵阳621900)
0 引 言
永磁同步电动机(以下简称PMSM)由于具有调速范围宽、能量密度高、过载能力强、效率高等特点,在大功率、高性能场合得到了广泛的应用。
PMSM 的运行特性受转子磁场谐波影响较大,尤其是在大功率、高精度的PMSM 应用场合[2-3]。电机模型作为研究控制系统运行特性的基础,人们通常希望在研究控制系统运行特性时,将影响电机运行特性的各种因素都考虑到模型中,特别是在研究大功率、高精度控制系统时。
常用的PMSM 模型通常是在气隙磁场为理想正弦分布的前提下建立的线性模型。这与真实电机相差较大,因而其仿真精度不高,降低了对实际控制系统的指导作用。
本文考虑转子磁场谐波的影响,建立了d、q 坐标系下的电机数学模型,并采用MATLAB /Simulink仿真系统,构建了考虑转子磁场谐波的永磁电动机模型。利用该模型,对某PMSM 进行了仿真,并对电机的转矩、转速特性与永磁同步电动机线性模型仿真结果进行了对比分析。分析结果证明了所建模型的正确性和有效性。
1 考虑转子磁场谐波的数学模型
1.1 PMSM 线性数学模型
d、q 轴电压平衡方程:
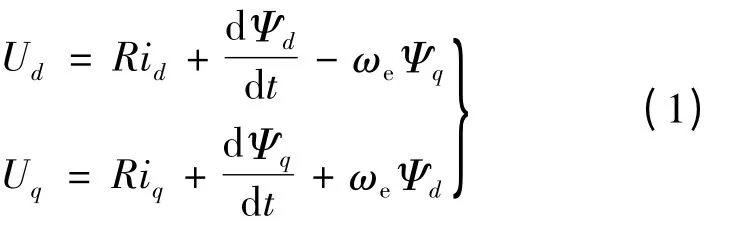
d、q 轴磁链方程:
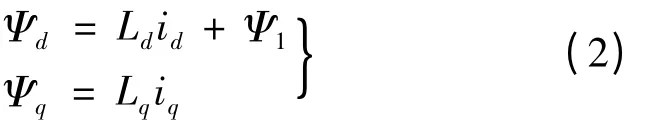
电磁转矩方程:
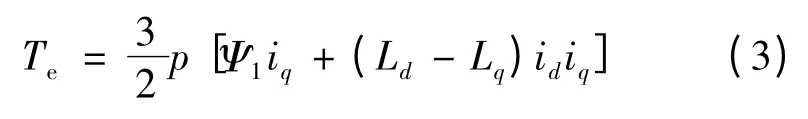
式中:Ψ1为永磁体基波磁链;Ld、Lq分别为d、q 电感。
1 .2 转子磁场谐波对PMSM 的影响
在PMSM 线性模型中,为了简化模型,将PMSM的转子磁场在气隙中的分布近似为正弦分布。但在电机的制造过程中,由于制造工艺的限制,永磁体产生的磁场含有大量的谐波成分,使得PMSM 的转子磁场在气隙中的分布并非理想的正弦分布[4]。可采用傅里叶变换将转子磁场分解得到:
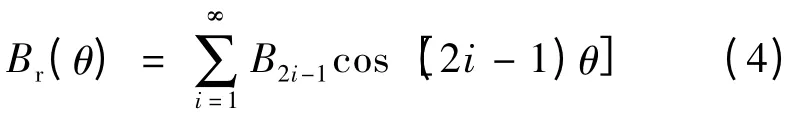
式中:θ 为d 轴与A 相轴线间的电角度。
因此,永磁体在一相定子绕组中产生的磁链可表示:
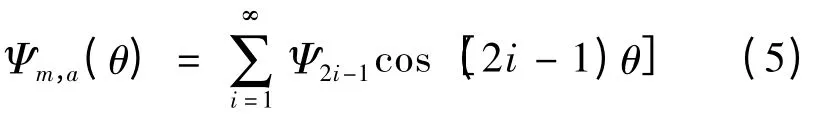
在d、q 坐标系下,d、q 轴磁链方程可表示:

从式(6)不难发现,出现了6 次谐波磁链[5]。d、q 轴电压平衡可表示:
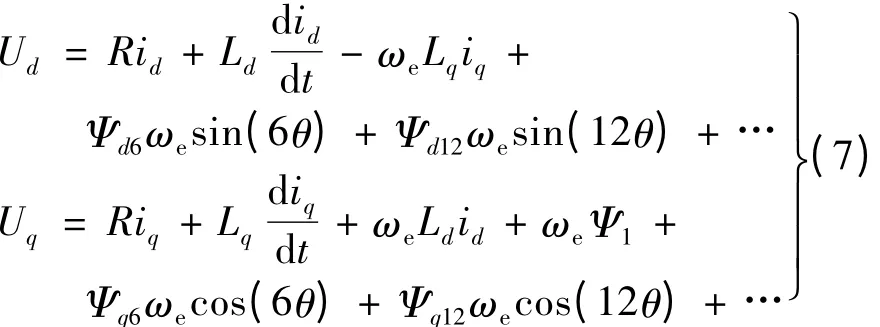
电磁转矩方程可表示:
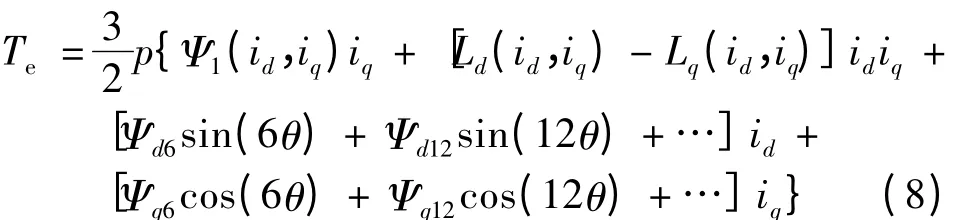
2 PMSM 建模
根据PMSM 考虑转子磁场谐波影响的数学模型,在MATLAB/Simulink 仿真环境下,建立仿真模型。
2.1 d、q 轴磁链方程和电压平衡方程建模
根据式(6)、式(7),输入变量为Ud、Uq、ωe,输出变量为id、iq。PMSM 电压、转速和电流关系模型如图1 所示。
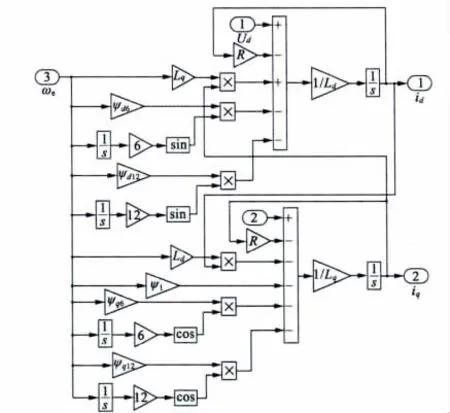
图1 PMSM 电压、转速和电流关系模型
2.2 电磁转矩方程建模
根据式(8),输入变量为id、iq、ωe,输出变量为Te,电磁转矩关系模型如图2 所示。
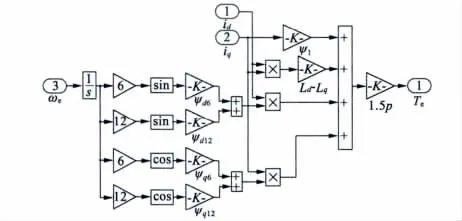
图2 电磁转矩关系模型
2.3 电机本体建模
电机本体模型除了由以上两个模块组成外,还需坐标变换模块,由于MATLAB /Simulink 中自带坐标变换模块,此处不对其进行详细叙述。电机本体模型如图3 所示。
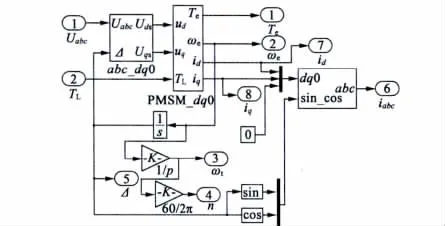
图3 电机本体模型
3 仿真分析
在MATLAB /Simulink 中,对某PMSM 分别采用线性模型和考虑转子磁场谐波的电机模型进行仿真分析。
仿真设置如下:采样时间间隔为20 μs,仿真时间为2.0 s。对电机施加理想正弦波电压,电压幅值和频率分别为380 V 和50 Hz。所仿真PMSM 参数如表1 所示。
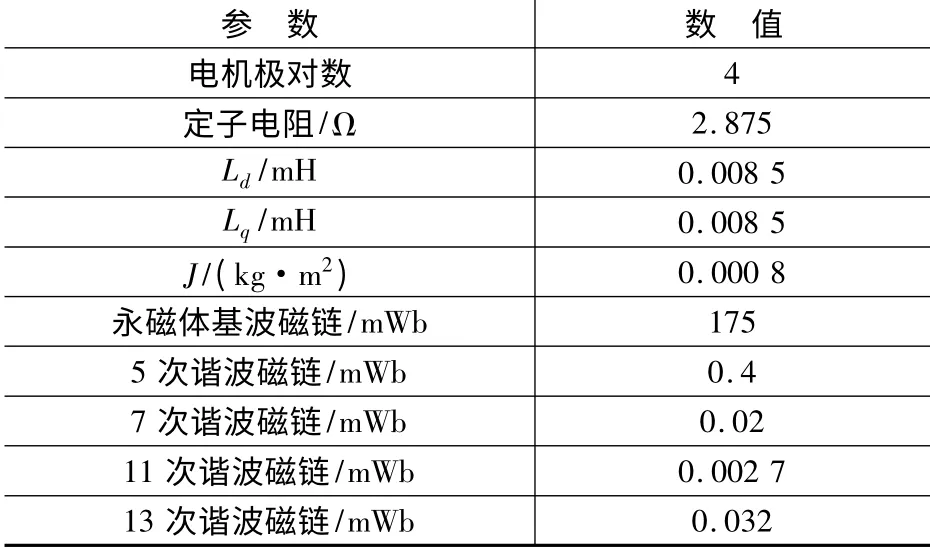
表1 PMSM 参数
图4、图5 分别为PMSM 线性模型和考虑转子磁场谐波的PMSM 模型的仿真结果。图中分别显示了PMSM 进入稳态后电动机的转矩Te和转速n曲线。
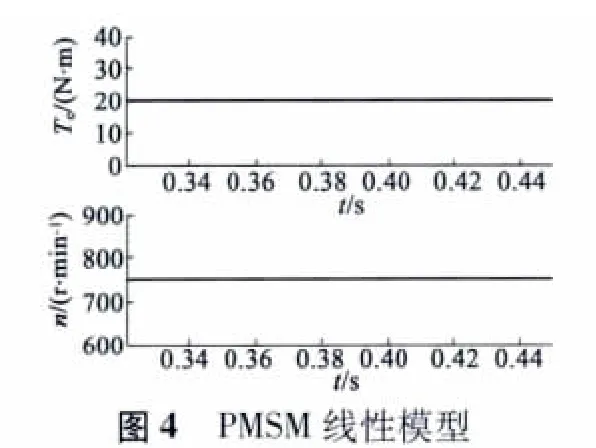

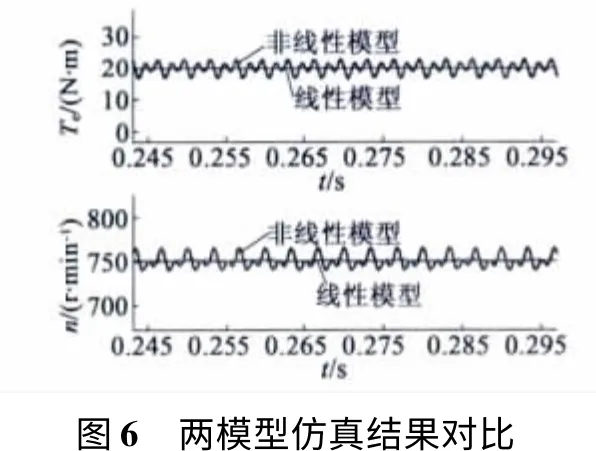
图6 对进入稳态后,两种电机模型进行了细微对比,在考虑转子磁场谐波的PMSM 模型中,转矩和转速波形均发生了明显的畸变,这正是由转子磁场中的谐波引起的。
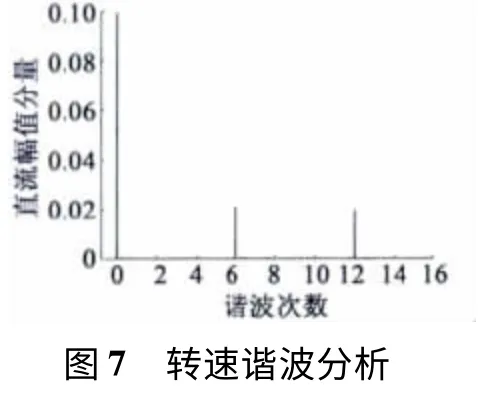
如图7 所示,对考虑磁场谐波的电机模型转速波形进行谐波分析,结果表明所含的谐波主要为基波的6k 次谐波,这是由于永磁同步电机的6k 次转矩脉动引起的6k 次转速波动。
本文中,为了简化问题,仅考虑了转子磁场中5、7、11、13 次谐波对电机电磁转矩和转速的影响。在电机模型中,考虑电机转子磁场谐波次数越多,越接近真实电机中磁场谐波对电机的影响。
4 结 语
本文对考虑转子磁场谐波的PMSM 数学模型以及MATLAB /Simulink 仿真模型的建立过程进行了详细的论述,并对同一PMSM 分别采用线性模型和考虑转子磁场谐波的非线性模型进行对比仿真。仿真结果表明,本文所建立的考虑转子磁场谐波的PMSM 模型在一定程度上反映出真实电机的转矩脉动和转速波形特性,为进一步研究PMSM 的精确控制仿真系统奠定了基础。
[1] Panda S K,Xu Jianxin,Qian Weizhe.Review of torque ripple minimization in PM synchronous motor drives[C]/ /Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century,USA,2008 IEEE.Pittsburgh,PA:IEEE,2008:1-6.
[2] 王兴华,励庆孚,王曙鸿.永磁无刷直流电机负载磁场及其电磁转矩的计算[J].中国电机工程学报,2003,23 (4):140 -144.
[3] Lee Ji-Young,Lee Sang-Ho,Lee Geun-Ho,et al.Determination of parameters considering magnetic nonlinearity in an interior permanent magnet synchronous motor[J].IEEE Trans.on Magnetic,2006,42(4):1303-1306.
[4] 唐任远.现代永磁电机理论与设计[M].1 版.北京:机械工业出版社,2005.
[5] 揭贵生,马伟明.考虑转子磁通谐波的永磁同步电机控制性能分析[J].铁道科学与工程学报,2005,2(6):92-97.

