利用密度泛函理论研究α-联噻吩体系H(C4H2S)nH的结构和电子光谱

宁 攀，赵建想

(河南大学 化学化工学院 环境和分析科学研究所，河南 开封 475004)

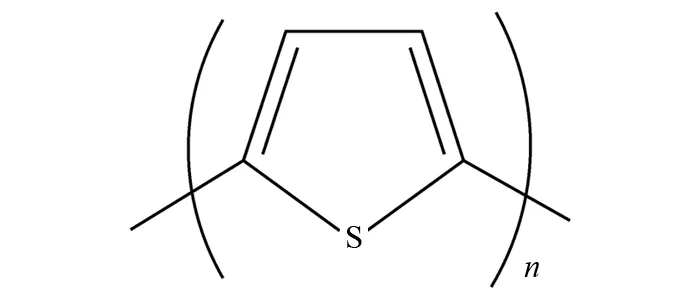
图1 α-联噻吩Fig.1 α-Oligothiophenes

在过去的几十年里，以α-位的C-C单键相连接的联噻吩(α-联噻吩)(如图1所示)由于其具有平面的或是类似线性的共轭π体系结构而被广泛研究[1-5]. 它们突出的光学、电学、氧化还原、光致发光和电荷传输等特性让它们在有机场效应晶体管[6]、发光二极管[7]以及光伏打电池[8-9]等方面表现出广泛的应用和发展前景. 早在1974年，KUHN等人[10]就报道了α-五联噻吩在Langmuir-Blodgett薄膜中的电流测量值；1999年，DENIS F等研究了α-联噻吩的晶体和薄膜结构[11]；2011年，SIEGERT等人利用光致光电子能谱法研究了在气相中将自由基阴离子接入中性α-联噻吩的最低电子激发态[12]. 但这些研究的对象都是八个噻吩环以内的α-联噻吩，对于含有八个以上噻吩环的α-联噻吩还未见报道.

为更好地了解噻吩环个数与其结构的关系，并预测较长的联噻吩体系的光谱性质，本文作者采用密度泛函理论优化了H(C4H2S)nH (n= 2～13)的基态和最低激发态的几何构型，在平衡构型的基础上进一步计算了它们的垂直激发能和垂直发射能.

1 计算方法

在B3LYP/6-31G(d)和CAM-B3LYP/ 6-31G(d)水平下优化了α-联噻吩 H(C4H2S)nH(n= 2～13)的基态几何构型，并在相同水平下计算了它们的振动频率. 采用TD-B3LYP和TD-CAM-B3LYP方法优化了它们的激发态. 用含时密度泛函理论的TD-B3LYP方法，分别结合cc-pVDZ, cc-pVTZ以及6-31G(d)基组计算了α-联噻吩H(C4H2S)nH (n= 2～13)的垂直跃迁能. 考虑到溶剂对有机分子光谱的影响，在计算的过程中使用了极化连续介质(PCM)模型[13-14]. 最后，在TD-CAM-B3LYP/cc-pVDZ和TD-CAM-B3LYP/cc-pVTZ水平下计算了它们的垂直发射能. 以上所有计算都是利用Gaussian 09程序完成的.

2 结果和讨论

2.1 基态几何构型和稳定性

本文中要讨论的α-联噻吩(以下简称α-nT，n代表噻吩环的个数)有三种构型，包括对称性为C1和C2的螺旋上升型和环型的两种顺式结构(以下分别简称cis-C1和cis-C2)以及对称性为C1的稍有弯曲的带状结构的反式构型(以下简称trans)，如图2，图3和图4所示. 利用B3LYP和CAM-B3LYP方法优化了α-nT的基态构型，这两种方法计算的结果非常接近，优化得到的C-C键的键长和二面角相差很小.

图2 α-联噻吩H(C4H2S)nH (n = 2～13) 的几何结构Fig.2 Structures of α-oligothiophenes H(C4H2S)nH (n = 2-13)

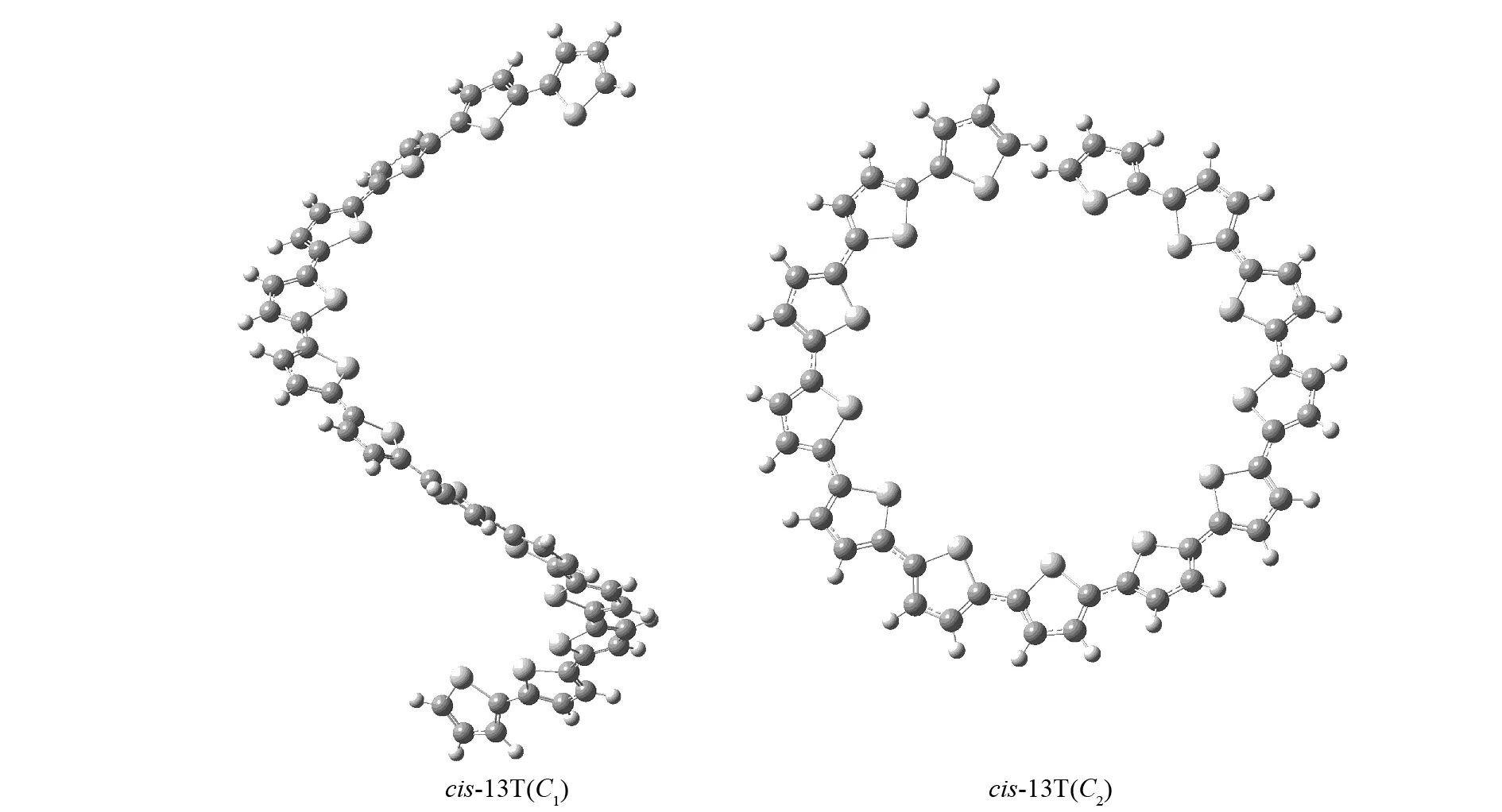
图3 B3LYP/6-31G(d) 方法下优化得到的cis-13T的基态构型Fig.3 Optimized structures of cis-13T at B3LYP/6-31G(d) level

图4 B3LYP/6-31G(d) 方法下优化得到的tran-13T的基态构型Fig.4 Optimized structures of tran-13T (S0) at B3LYP/6-31G(d) level

B3LYP和CAM-B3LYP两种方法计算得到的振动频率都是正值，说明优化得到的结构对应势能面上的能量极小点，均是稳定构型. 而且它们的最小弯曲振动频率都小于100 cm-1，可见此类化合物是“非刚性的”，而且随着n的增加，弯曲振动频率逐渐减小，化合物会越来越“软”.

2.2 基态和激发态的比较

TD-B3LYP方法优化的α-nT (n= 10)的第一激发态21A (21B)的构型绘制于图5.cis-C1和cis-C2构型由基态的螺旋上升型和环型结构变成了激发态的环状结构. 第一激发态的相邻噻吩环之间的二面角接近于0°或180°,即近似于平面；而C-C键的键长跟基态相比均变小，这种缩短是由于激发态分子的平面性增强，电子离域程度增大导致的. TD-CAM-B3LYP方法优化的结果也是如此.

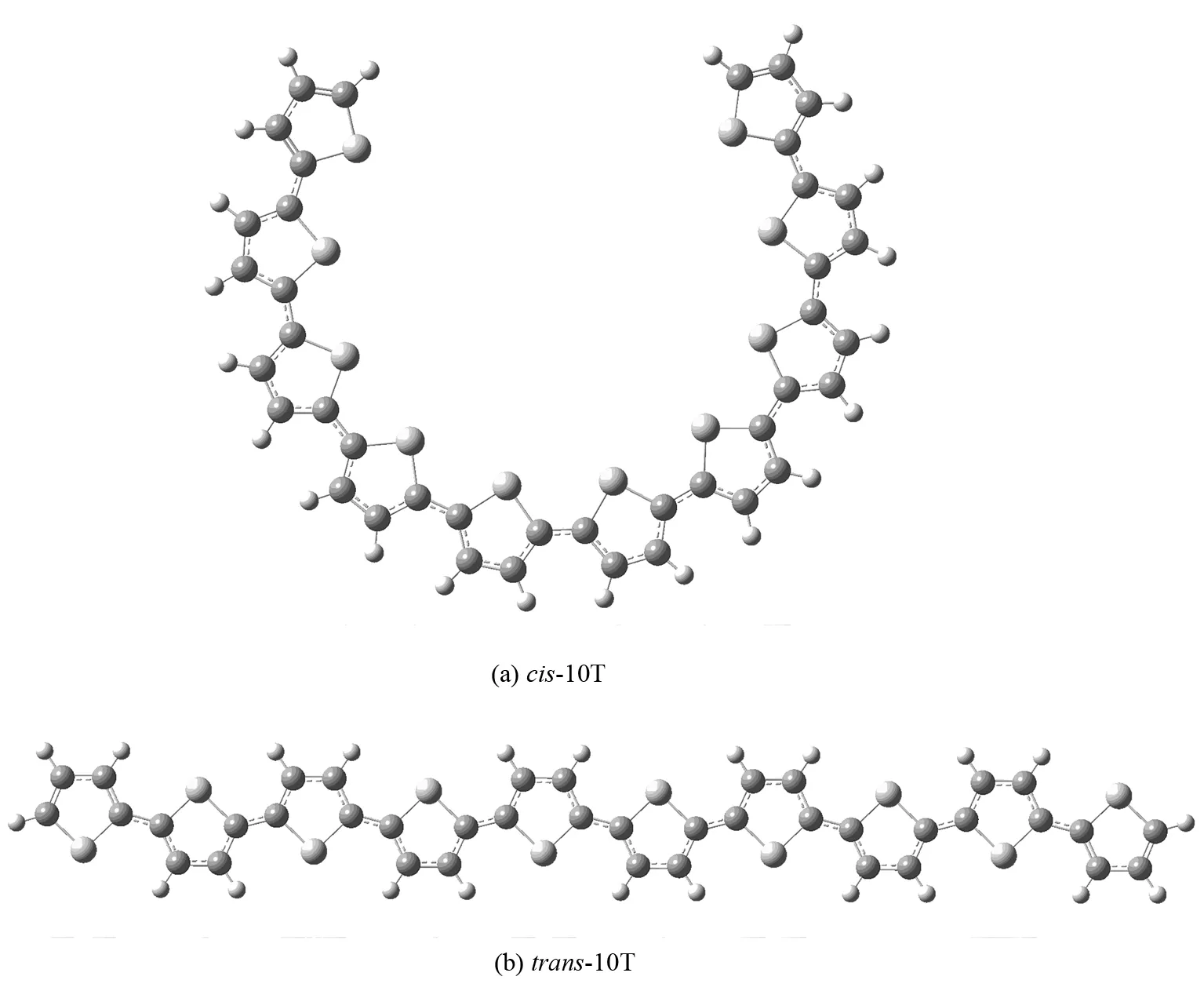
图5 TD-B3LYP方法下优化得到的α-10T的第一激发态的构型Fig.5 Optimized structures of α-10T (S1) at TD-B3LYP/6-31G(d) level

2.3 能隙

图6是体系在气相中运用B3LYP方法得到的HOMO，LUMO能量及其能隙ε与n的关系图. 从图中可以看出，随着n的增加，体系的HOMO能量逐渐升高，而LUMO能量则逐渐降低，因此LUMO与HOMO的能量差逐渐减小，我们推测是由于体系的共轭程度随着n的增大而增强，导致前线轨道的能隙ε减小，从HOMO到LUMO的电子跃迁逐渐变得容易，从而导致吸收波长增长.

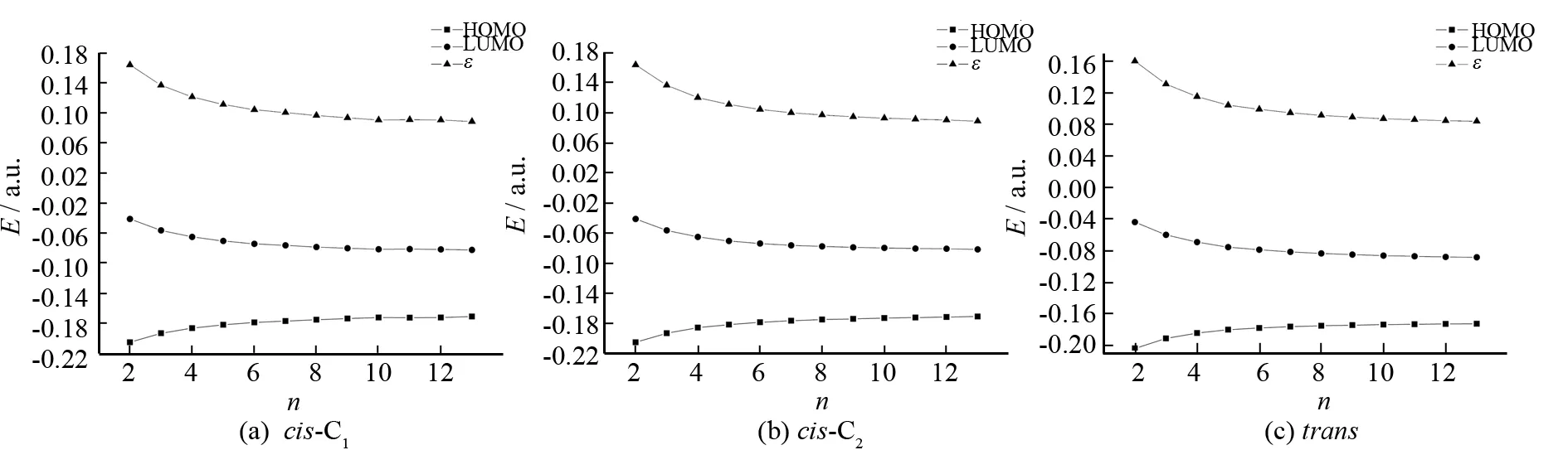
图6 B3LYP方法下得到的气相中的α-nT的HOMO能量，LUMO能量和能隙εFig.6 The energy levels of HOMO, LUMO and ε of α-nT by B3LYP method in gas phase

2.4 垂直跃迁能

表1-表3列出了TD-B3LYP方法分别结合cc-pVDZ, cc-pVTZ 以及 6-31G(d)基组计算得到的α-nT (n= 2～13)的21A (21B)←X1A电子跃迁的垂直跃迁能和相应的实验值.

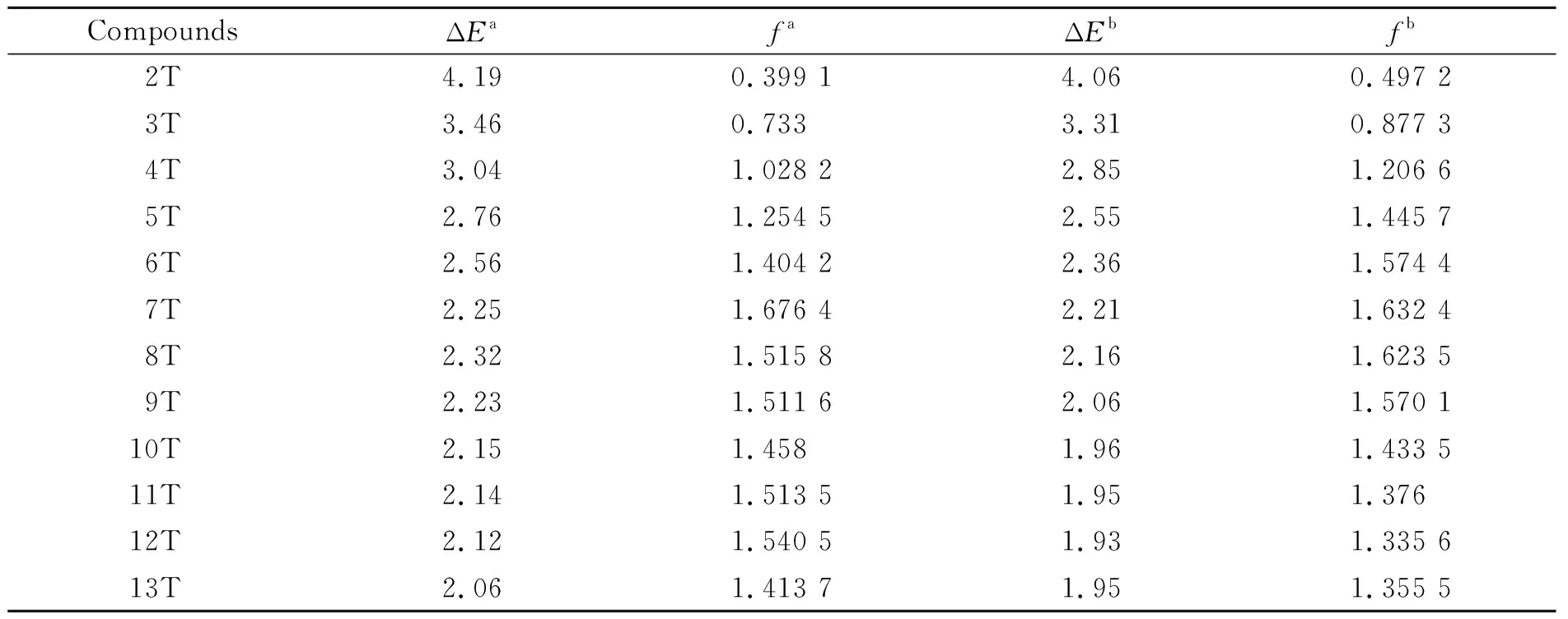
表1 cis-α-nT (C1)的S0→S1的垂直跃迁能(ΔE,eV)和振子强度(f)Table 1 The vertical transition energies (ΔE, eV) and oscillator strengths (f) of cis-α-nT (C1) of S0→S1

aBy TD-B3LYP/cc-pVDZ in gas;bBy TD-B3LYP/cc-pVDZ in dichloromethane

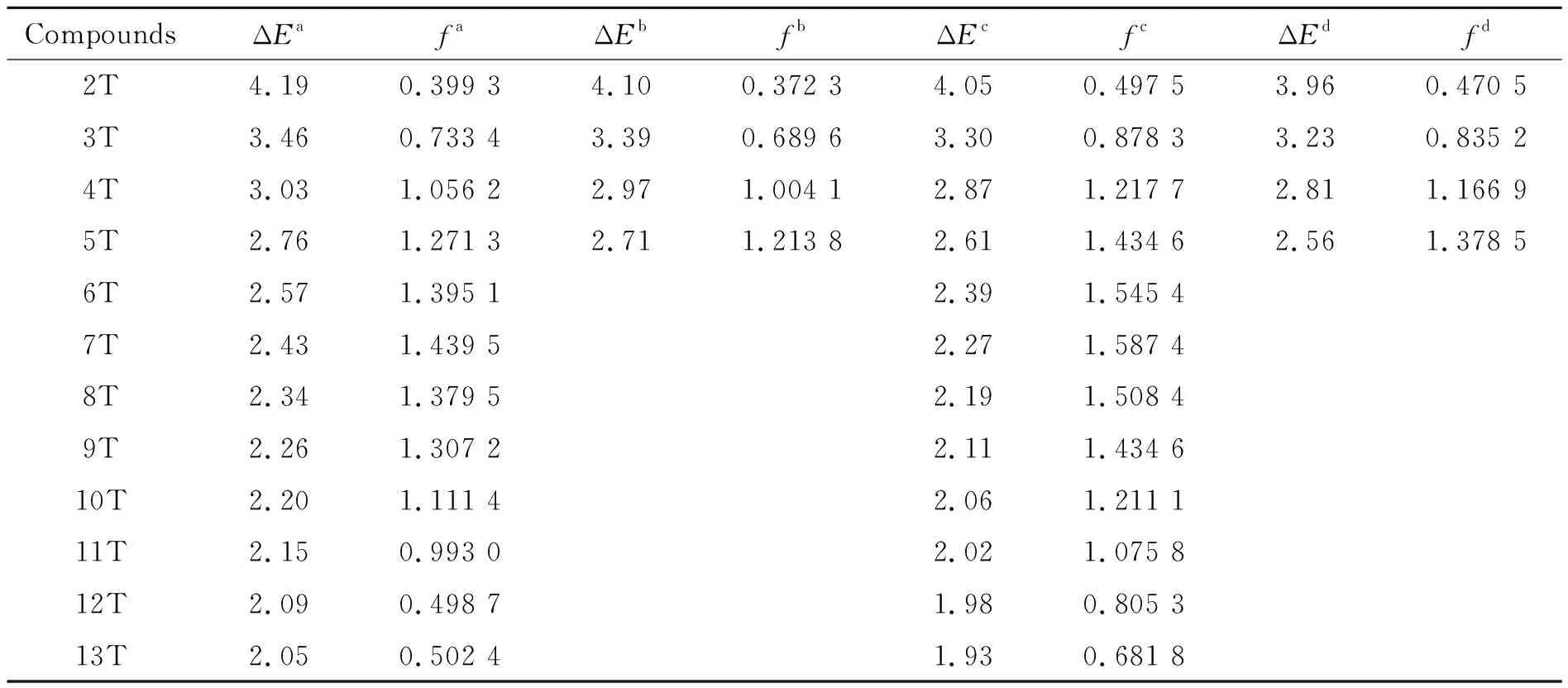
表2 cis-α-nT (C2)S0→S1的垂直跃迁能(ΔE, eV)和振子强度(f)Table 2 The vertical transition energies (ΔE, eV) and oscillator strengths (f) of cis-α-nT (C2) of S0→S1

aBy TD-B3LYP/cc-pVDZ in gas;bBy TD-B3LYP/cc-pVTZ in gas;

cBy TD-B3LYP/6-31G(d) in dichloromethane;

dBy TD-B3LYP/cc-pVTZ in dichloromethane

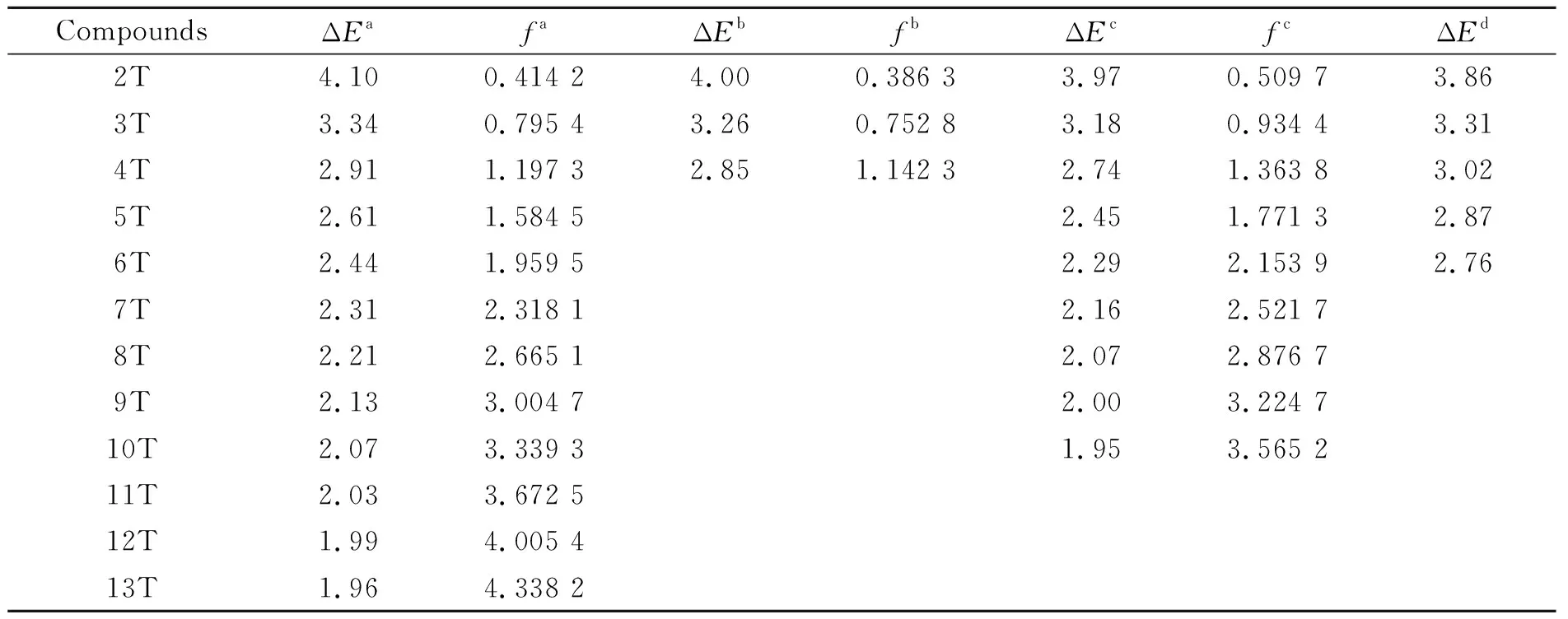
表3 trans-α-nT (n = 2～13)S0→S1的垂直跃迁能(ΔE, eV)和振子强度(f)和实验值Table 3 The vertical transition energies (ΔE, eV) and oscillator strengths (f) of trans-α-nT(n =2-13) of S0→S1 and the experimental value

aBy TD-B3LYP/cc-pVDZ in gas;bBy TD-B3LYP/cc-pVTZ in gas;

cBy TD-B3LYP/cc-pVDZ in dichloromethane;d实验值摘自参考文献[12]

2.4.1 cis-α-nT (C1)

表1列出了气相和二氯甲烷溶剂中在TD-B3LYP/cc-pVDZ水平下计算得到的cis-α-nT (C1) (n= 2～13)的21A (21B)←X1A电子跃迁的垂直跃迁能. 表中数据显示，随着n的增加，除了7T以外，垂直跃迁能逐渐减小，这表明21A (21B)←X1A电子跃迁随着n的增大变得越来越容易，图6很直观的描述了这一现象.

因为激发态21A (21B)都是由HOMO→LUMO的电子跃迁引起的，所以cis-α-nT (C1)的能隙与21A (21B)←X1A跃迁的跃迁能递减的趋势密切相关. 由图7可见，随着噻吩环个数n的增加，21A (21B)←X1A跃迁的垂直跃迁能逐渐减小，并趋于平缓，这与HOMO-LUMO能隙变化趋势是一致的.

2.4.2 cis-α-nT (C2)

在不同水平下计算的cis-α-nT (C2) (n= 2～13)的21A (21B)←X1A电子跃迁的垂直跃迁能结果列于表2中. 数据表明，不同的基组和溶剂对此体系的跃迁能影响不大.

在TD-B3LYP/cc-pVDZ方法下计算的相邻跃迁能之间的差值为：0.73, 0.43, 0.27, 0.19, 0.14, 0.09, 0.08, 0.06, 0.05, 0.06 和 0.04 eV. 从这些数据可以看出，随着n的增大，跃迁能呈现递减的趋势. 在此方法下计算的跃迁能与体系大小n的依赖关系绘于图8.

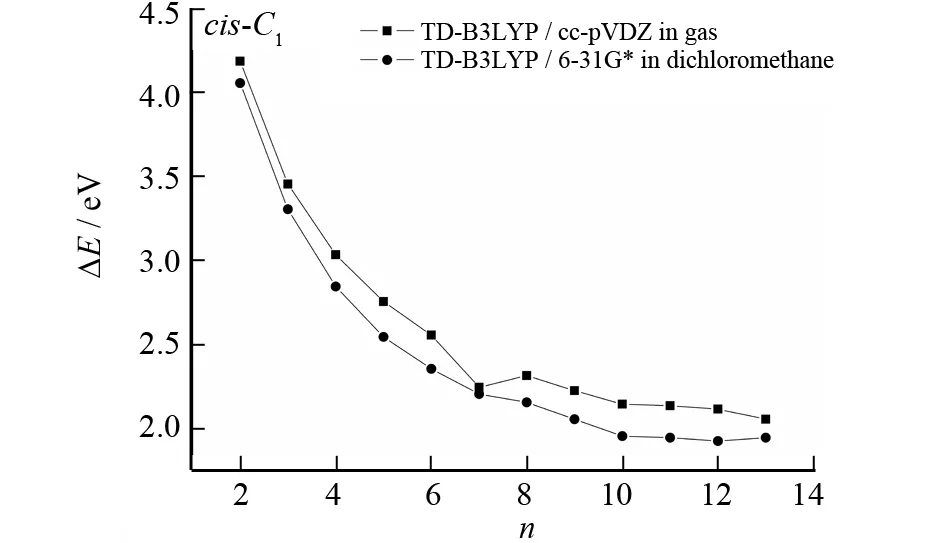
图7 cis-α-nT (C1)的21A (21B)←X1A的垂直跃迁能与n的关系曲线Fig.7 Plot of the vertical transition energies of the 21A (21B)←X1A transition for cis-α-nT (C1) vs n

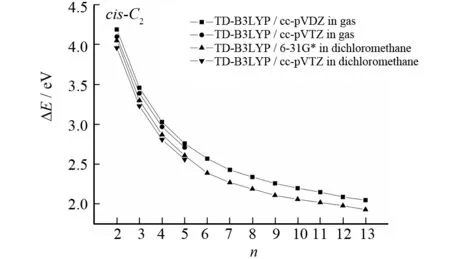
图8 cis-α-nT (C2)的21A (21B) ←X1A的垂直跃迁能与n的关系曲线Fig.8 Plot of the vertical transition energies of the 21A (21B)←X1A transition for cis-α-nT (C2) vs n

从图8中可知体系跃迁能与体系大小n呈现非线性关系. 拟合表2中在TD-B3LYP/cc-pVDZ水平下得到的跃迁能数据，得到cis-α-nT (C2) (n= 2～13)体系气相中的21A (21B)←X1A跃迁能和体系大小n的关系式：

ΔE=A+B1e-n/D1+B2e-n/D2

(1)

式中，A= 1.685 39,B1= 1.451 12,B2= 4.486 21,D1= 9.411 89, 和D2= 1.644 97. 拟合误差和相关系数分别为0.000 03 eV和 0.999 95. 用式(1)可以预测，当体系足够大时，体系的跃迁能ΔE将收敛至1.68 eV (735.57 nm). 为了更好的说明这种非线性关系，其他水平下计算的跃迁能与体系大小n的依赖关系也绘于图7中.

2.4.3 trans-α-nT

表3列出了在不同理论水平下计算得到的trans-α-nT (n= 2～13)的21A←X1A电子跃迁的垂直跃迁能(ΔE)，振子强度(f)和相应的实验值. 由表3数据可知，理论计算的2T-4T的垂直跃迁能与实验值符合得很好，但是随着链的增长误差越来越大. 表4列出了以前的理论研究和实验上得到的trans-α-nT的第一激发态的跃迁能数据以及本文中的理论值. 从表中数据可以发现，在TD-B3LYP/cc-pVDZ和TD-B3LYP/cc-pVTZ水平下计算得到的数据与先前报道的DFT/MRCI和 CASPT2 方法下计算结果都很接近. 考虑到计算成本，我们在TD-B3LYP/cc-pVTZ水平下计算了n= 2～4的联噻吩体系.

表4 气相中的第一单重激发态能量(eV)Table 4 The S1 singlet state vertical transition energies in gas phase (all energies in eV)

aBy TD-B3LYP/cc-pVDZ;bBy TD-B3LYP/cc-pVTZ;

cCASPT2// MP2, 摘自参考文献 [15-16];dtrans-α-2T气相中的LIF光谱, 摘自参考文献 [17];

eDFT/MRCI, 摘自参考文献 [12];f摘自参考文献 [12]

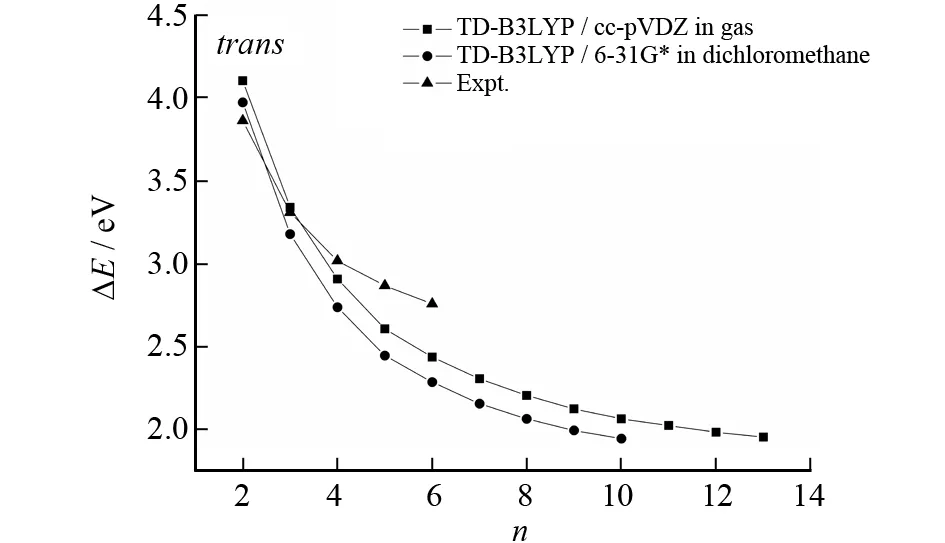
实验值摘自参考文献[12]图9 trans-α-nT的21A←X1A的垂直跃迁能与n的关系曲线Fig.9 Plot of the vertical transition energies of the 21A←X1A transition for trans-α-nT vs n

图9trans-α-nT是在TD-B3LYP/cc-pVDZ水平下气相和二氯甲烷溶剂中的21A←X1A垂直跃迁能与体系大小n的关系. 从预测的垂直跃迁能可以看出，随着n的增大能量在逐渐减小，说明随着n的增加21A←X1A电子跃迁越来越容易.

将气相和二氯甲烷溶剂中TD-B3LYP/cc-pVDZ水平下得到的垂直跃迁能数据用公式(1)进行拟合，可以得到: 在气相中，A=1.830 79,B1=1.930 39,B2=4.309 28,D1=4.800 47, 和D2=1.365 59；拟合误差和相关系数分别为0.000 05 eV和 0.999 93. 当体系足够大时，ΔE将收敛至1.83 eV (677.45 nm)；在二氯甲烷溶剂中，A=1.756 45,B1=1.917 29,B2=4.694 34,D1=4.337 55 和D2=1.297 1；拟合误差和相关系数分别为0.000 05 eV和0.999 94. 当体系足够大时，ΔE将收敛至1.75 eV (708.42 nm). 这说明溶剂对体系的垂直跃迁能有一定的影响.

从图8可以看出，不同水平下计算的垂直跃迁能在n比较小的时候与实验值符合得很好，但随着链的增长，与相应的实验结果之间的误差在增加.

2.5 垂直发射能

在TD-CAM-B3LYP方法优化的第一激发态构型的基础上，计算了α-联噻吩 H(C4H2S)nH (n= 2～10)的21A (21B)→X1A的电子发射能. 利用TD-CAM-B3LYP/cc-pVDZ 和TD-CAM-B3LYP/cc-pVTZ方法计算的发射波长λ(nm)和振子强度f以及相应的实验值列在表5中. 不同水平下计算的发射波长相互之间很接近，而且都跟实验值符合得较好，说明TD-CAM-B3LYP方法是计算发射光谱的一种行之有效的方法. 计算的发射光谱与相应的吸收光谱相比呈现明显的红移，是由于激发态弛豫造成的.

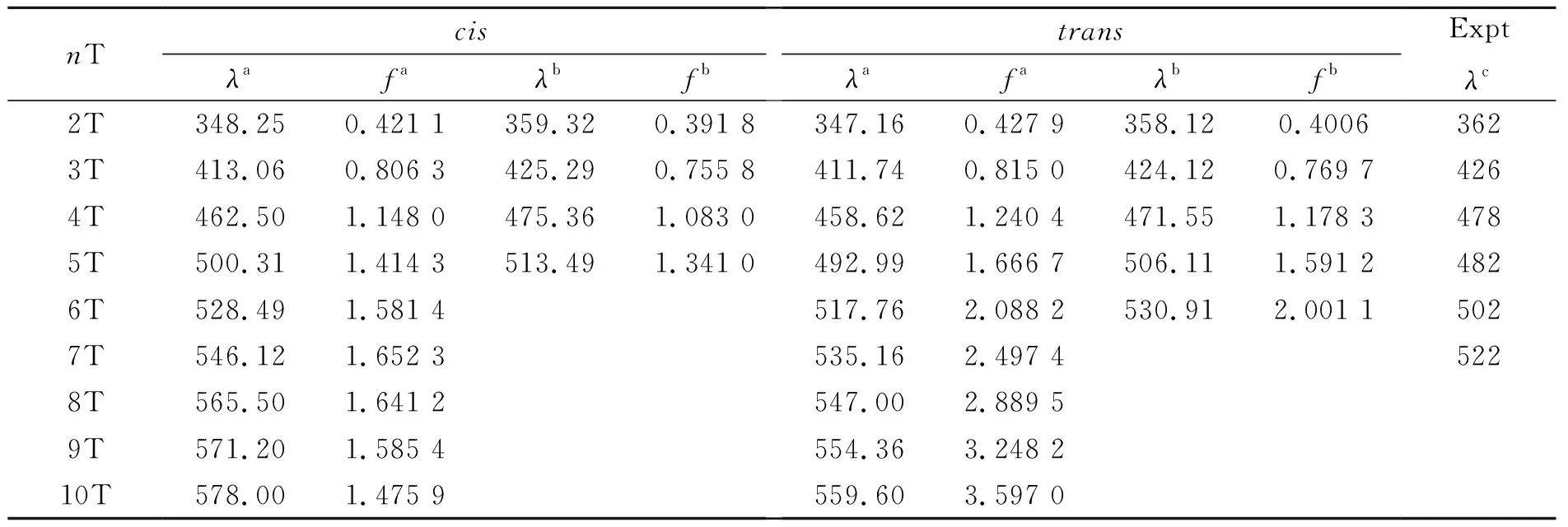
表5 TD-CAM-B3LYP计算的α-nT 的垂直发射能(nm)和振子强度以及相应的实验值Table 5 The vertical emission energies (λ in nm) and oscillator strengths (f) of α-nT at TD-CAM-B3LYP level, along with the experimental value

aBy TD-CAM-B3LYP/cc-pVDZ;bBy TD-CAM-B3LYP/cc-pVTZ;c摘自参考文献[18]

3 结论

分别运用B3LYP/6-31G(d) 和 CAM-B3LYP/6-31G(d)两种密度泛函理论优化了α-联噻吩H(C4H2S)nH (n= 2～13)的基态构型. 振动频率分析结果表明得到的三种结构都是稳定构型. 用TD-DFT方法优化了对应的第一激发态的平衡构型，与基态相比，激发态构型中C-C键的长度缩短了，这是由于激发态分子的平面性增强，电子的离域程度增大导致的.

在TD-B3LYP/cc-pVDZ、TD-B3LYP/cc-pVTZ和TD-B3LYP/6-31G(d)三种理论水平下，预测的α-联噻吩体系三种构型的21A (21B) ←X1A跃迁的垂直跃迁能都具有相似的非线性尺寸依赖. 根据计算结果，导出了这个体系的垂直跃迁能与体系大小n的解析关系式.

体系的垂直发射能是在TD-CAM-B3LYP/cc-pVDZ 和 TD-CAM-B3LYP/cc-pVTZ水平下计算得到的，预测的最大发射波长与相应的实验值符合得较好. 上述结果将为进一步研究更长的联噻吩体系的发光性质提供必要的理论信息.

参考文献：

[1] CASADO J, PAPPENFUS T M, MILLER L L, et al. Nitro-functionalized oligothiophenes as a novel type of electroactive molecular material: spectroscopic, electrochemical, and computational study[J]. J Am Chem Soc, 2003, 125(9): 2524-2534.

[2] ZHANG Xin Nian, MATZGER A J. Effect of ring fusion on the electronic absorption and emission properties of oligothiophenes[J]. J Org Chem, 2003, 68(25): 9813-9815.

[3] CARAS-QUINTERO D, BAUERLE P. Synthesis of the first enantiomerically pure and chiral, disubstituted 3,4-ethylenedioxythiophenes (EDOTs) and corresponding stereo-and regioregular PEDOTs[J]. Chem Commun, 2004 (8): 926-927.

[4] MURPHY A R, FRECHET J M J, CHANG P, et al. Organic thin film transistors from a soluble oligothiophene derivative containing thermally removable solubilizing groups[J]. J Am Chem Soc, 2004, 126(6): 1596-1597.

[5] ZHANG Xin Nian, CTÉA P, MATZGER A J. Synthesis and structure of fusedα-oligothiophenes with up to seven rings[J]. J Am Chem Soc, 2005, 127(30): 10502-10503.

[6] BRUSSO J L, HIRST O D, DADVAND A, et al. Two-dimensional structural motif in thienoacene semiconductors: synthesis, structure, and properties of tetrathienoanthracene isomers[J]. Chem Mater, 2008, 20(7): 2484-2494.

[7] PEREPICHKA I F, PEREPICHKA D F, MENG H. Light-emitting polythiophenes[J]. Adv Mater, 2005, 17(19): 2281-2305.

[8] KWON T H, ARMEL V, NATTESTAD A, et al. Dithienothiophene (DTT)-based dyes for dye-sensitized solar cells: synthesis of 2,6-dibromo-DTT[J]. J Org Chem, 2011, 76(10): 4088-4093.

[9] BOUDREAULT P L T, NAJARI A, LECLERC M. Processable low-bandgap polymers for photovoltaic applications[J]. Chem Mater, 2011, 23: 456-469.

[10] SCHOELER U, TEWS K H, KUHN H. Potential model of dye molecule from measurements of the photocurrent in monolayer assemblies[J]. J Chem Phys, 1974, 61: 5009.

[11] FICHOU D. Structural order in conjugated oligothiophenes and its implications on opto-electronic devices[J]. J Mater Chem, 2000, 10: 571-588.

[12] SIEGERT S, VOGELER F, MARIAN C M, et al. Throwing light on dark states ofα-oligothiophenes of chain lengths 2 to 6: radical anion photoelectron spectroscopy and excited-state theory[J]. Phys Chem Chem Phys, 2011, 13: 10350-10363.

[14] TOMASI J, PERSICO M. Molecular interactions in solution: an overview of methods based on continuous distributions of the solvent[J]. Chem Rev, 1994, 94(7): 2027-2094.

[15] RUBIO M, MERCHN M, POU-AMÉRIGO R, et al. The low-lying excited states of 2,2′-bithiophene: a theoretical analysis[J]. Chem Phys Chem, 2003, 4(12): 1308-1315.

[16] RUBIO M, MERCHN M, ORTI E. A theoretical study on the low-lying excited states of 2,2′:5′,2″-terthiophene and 2,2′:5′,2″:5″,2‴-quaterthiophene[J]. Chem Phys Chem, 2005, 6(7): 1357-1368.

[17] BIRNBAUM D, FICHOU D, KOHLER B E. The lowest energy singlet state of tetrathiophene, an oligomer of polythiophene[J]. J Chem Phys, 1992, 96: 165-169.

[18] BECKER R S, MACANITA A L, ELISEI F, et al. Comprehensive evaluation of the absorption, photophysical, energy transfer, structural, and theoretical properties ofα-oligothiophenes with one to seven rings[J]. J Chem Phys, 1996, 100(48): 18683-1869.