基于改进模式搜索法的毁歼概率误差参数自寻优组合
刘 恒,梅 卫,单甘霖,张小伟
(1.军械工程学院,河北 石家庄 050003,2.西安军代局驻咸阳地区军代室,陕西 咸阳 712099)
对付诸如巡航导弹、制导炸弹等低空、超低空目标,小口径高炮的着发命中是最有效的末端拦截手段[1],具有不可替代性[2]。对目标的毁歼概率指标是衡量一个高炮武器系统综合作战能力高低的核心指标[3],也是设计人员在高炮武器系统设计阶段,对各个分系统进行精度分配、参数匹配等优化设计的主要依据。通常情况下,使毁歼概率达到最大的参数组合方式,应该就是方案设计寻求的可接受解[1]。同时参考文献[4]也指出:误差参数特性存在一组最佳匹配关系,使毁歼概率达到最大。但未给出具体的方法来选择具有最佳匹配关系的误差参数组合。模式搜索法是解决优化问题的一种搜索方法,由Hooks和Jeeces(1961)提出,它并不需要任何目标函数的梯度信息[5-7],适合解决文中所提的问题。
笔者首先构建基于毁歼概率寻优的误差参数自匹配计算模型,然后,提出解算模型的寻优算法——改进模式搜索法。最后,进行数字仿真验证改进模式搜索算法的有效性。
1 毁歼概率数学模型的构建
文中考虑的是着发射击高炮系统的毁歼概率,故以参考文献[3]中提出的毁歼概率计算模型为基础,这里对此模型作简单介绍。

(1)
式中:


(2)
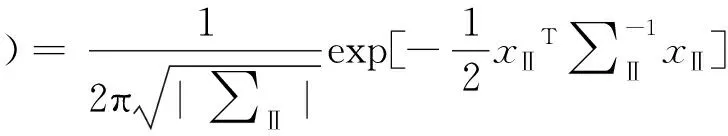
(3)
式中:m为高炮门数;p为单炮炮管数;n为每个炮管发射的弹丸数;w为毁歼目标所需的平均命中弹数;l为目标投影等效成矩形边长的一半。
2 计算模型及改进模式搜索寻优算法
毁歼概率计算模型中的误差参数包括:系统误差a、火炮点射散布误差均方差σ、火控计算机输出误差均方差σO、稳定装置误差均方差σT和火炮传动装置误差均方差σP共5种[3]。参数匹配计算步骤是:首先确定高炮系统5种误差参数的取值范围,分别记为[lbiubi],i=1,2,…,5;在该取值范围内,分别调整各个参数的值,形成不同的参数组合,然后计算每一组参数组合下的毁歼概率Pkill。经过比较,选择出使毁歼概率达到最大值的参数组合方式,即是最佳匹配的误差参数组合。建立如下数学模型:
(4)
式(4)中的目标函数根据式(1)~(3)计算。
(1)澳大利亚灯桩设计建设。澳大利亚航标结构多样化,但其海事当局在灯桩设计建设采用和推荐结构有—四桩式钢混结构平台灯桩、单桩式钢混结构灯桩。其发展的思路是性能可靠、维护简单或免于维护。
毁歼概率计算过程比较复杂,不易计算其导数等信息。模式搜索法是解决优化问题的一种搜索方法,由Hooks和Jeeces(1961)提出,它并不需要任何目标函数的梯度信息[5-7]。它由两类“移动”组成:一是“探测性”移动,另一是“模式性”移动。探测性移动是以一定的步长沿着轴向探测,目的是揭示目标函数的变化规律,探测函数的下降方向;而模式性移动是沿着有利方向直接搜索,目的是利用发现的函数变化规律寻找更好的点。计算步骤[7]如下:
Step1 选取初始数据。初始点x0,初始步长δ0>0,给定收缩因子α∈(0,1),给定允许误差ε>0,令k=0。
Step2 确定参考点。令y=xk,j=1。
Step3 正轴向探测。从点y出发,沿ej作正轴向探测:若f(y+δkej) Step4 负轴向探测。从点y出发,沿ej作负轴向探测:f(y+δkej) Step5 检验探测次数。若j Step6 进行模式移动。若f(xk+1) Step7 检查是否满足终止准则。若δk<ε,迭代终止,得近似最优解xk;否则,转Step8。 Step8 缩短步长。若xk+1=xk,令δk+1=αδk,k=k+1 ,返回Step2;否则,令xk+1=xk,δk+1=δk,k=k+1 ,返回Step2。 模式搜索法的终止迭代条件、迭代步长与算法的精度和速度都有很大关系,结合上文所构建模型的特点,提出改进的模式搜索法。以MATLAB中自带patternsearch函数为基础,作如下改进:TolX的取值为0.3;TolFun的取值为10-4;TolMesh的取值为0.2;TolCon的取值为10-2,这些值的选取是经过大量仿真,由经验得到。 为简便并不失一般性,在误差参数自匹配计算模型中,假设火控计算机输出误差均方差σO、稳定装置误差均方差σT和火炮随动系统输出误差均方差σP为固定值,仅以高炮系统误差a和火炮点射散布误差均方差σ为例,选择使毁歼概率最大的参数组合方式,研究两者之间的最佳匹配关系。 选取典型的水平匀速直线航路,高度H=1 000 m,航路捷径dj=500 m,斜距离D=1 500 m,速度v=250 m/s,参数选择的推导过程见参考文献[8],在此不再赘述。高炮系统误差a的取值范围是[2 8]mil,火炮点射散布误差均方差σ的取值范围是[2 8]mil,其余仿真条件参数见参考文献[3]中第6.2节。 仿真1:误差参数最佳组合的存在性 通过仿真方法求出误差参数最佳组合以及与之对应的毁歼概率最大值,证明存在误差参数的最佳组合,并将其作为基准值检验改进模式搜索算法等优化算法的计算精度。 仿真结果如图1所示,其中(a)图表示系统误差取[2 8]mil、弹丸散布误差均方差取[2 8]mil(记为第1组数据)时目标函数值的网眼图和等值线图;(b)图是与(a)图对应的目标函数曲面等高线图,在图中与目标函数最大值对应的横纵轴取值即为最优的误差参数组合;(c)图表示系统误差固定为3mil、弹丸散布误差均方差取[2 8]mil(记为第2组数据)时目标函数值变化规律图;(d)图表示弹丸散布误差均方差固定为4mil、系统误差取[2 8]mil(记为第3组数据)时目标函数值变化规律图。 分析图1可以看出,3种情况下均存在误差参数的最佳组合,分别是: 1)系统误差和弹丸散布误差均方差为(2.0 2.6)mil,与之对应的毁歼概率最大值为0.594 1。 2)系统误差和弹丸散布误差均方差为(3 2.7)mil,与之对应的毁歼概率最大值为0.561 1。 3)系统误差和弹丸散布误差均方差为(2 4)mil,与之对应的毁歼概率最大值为0.570 1。 仿真2:改进模式搜索法与其他优化算法性能比较 对算法的性能比较,选择计算精度和实时性两个指标,且更侧重于实时性。表1中的模拟退火算法、遗传算法和极小化极大值算法均来源于MATLAB中现成函数,仿真结果如表1所示。 表1 仿真数据 结果分析: 1)以仿真1中得到的误差参数最佳组合为基准值,检验各种算法的计算精度。可知,无论哪组仿真条件,模式搜索算法、模拟退火算法、遗传算法和极小化极大值4种算法的计算结果(包括误差参数组合和毁歼概率值)与基准值一致,精度最高。与毁歼概率最大值相比,三组仿真条件下改进模式搜索算法的计算结果与其相对误差分别是0.02%、0.07%和0,三者的平均值仅为0.03%,故可以忽略不计。这表明改进模式搜索算法的计算精度也非常高。 2)比较5种算法的计算耗时,改进模式搜索算法耗时最短,尤其是与极小化极大值算法、遗传算法和模拟退火算法相比,计算量显著减少,这说明该算法更具有实用性。 本文主要研究了高炮系统误差参数的最优匹配问题,提出了一种选择误差参数最佳组合的方法——改进模式搜索算法。通过仿真可知,改进模式搜索法在计算精度略微降低的同时,大幅度减少了计算时间,是可行有效的。 [1] 龙德和. 某自行高炮武器系统命中概率分析[D]. 南京:南京理工大学,2007. LONG De-he. Hit probability analysis of a self-propelled anti-air artillery weapon system[D]. Nanjing: Nanjing University of Science and Technology, 2007.(in Chinese) [2] 薄煜明,郭治,杜国平,等.高炮与防空导弹在近程防空反导中的互补性[J].兵工学报,2002,23(2):164-166. BO Yu-ming, GUO Zhi, DU Guo-ping, et al. Complementation of archibald and antiaircraft missile in low range air and anti-missile defence[J]. Acta Armamentarii, 2002, 23(2):164-166. ( in Chinese) [3] 肖元星,张冠杰. 地面防空武器系统效费分析[M]. 北京:国防工业出版社, 2006. XIAO Yuan-xing, ZHANG Guan-jie. Effectiveness-cost analysis on land-based air defens weapon system[M]. Beijing: National Defense Industry Press, 2006. ( in Chinese) [4] 薛德庆,赵斌,白向华. 误差特性对着发射击毁歼概率影响的仿真[J]. 四川兵工学报,2010,31(10):12-14. XUE De-qing, ZHAO Bin, BAI Xiang-hua. Simulation of influence for impact fire kill probability by error characteristic[J].Journal of Sichuan Ordnance, 2010,31(10):12-14. ( in Chinese) [5] 谢政,李建平,陈挚. 非线性最优化理论与方法[M]. 北京:高等教育出版社,2010. XIE Zheng, LI Jian-ping, CHEN Zhi. Nonlinear optimization theory and methods[M]. Beijing: Higher Education Press,2010. (in chinese) [6] WU T, SUN L P. A Filter-based pattern search me-thod for unconstrained optimization[J]. Numerical Mathematics, 2005, 15(3): 209-216. [7] 韩丽霞,王宇平,兰绍江. 基于模式搜索的类电磁算法求解约束优化问题[J]. 系统工程与电子技术,2009, 31(9):2219-2222. HAN Li-xia, WANG Yu-ping, LAN Shao-jiang. Electromagnetism-like method based on pattern search for constrained optimization problem[J]. Systems Engineering and Electronics,2009, 31(9):2219-2222. ( in Chinese) [8] 赵斌,薛德庆. 飞行目标参数对高炮武器系统着发射击毁歼概率的影响[J]. 火炮发射与控制学报,2010(1):1-3. ZHAO Bin, XUE De-qing. Influence of flight target parameter on impact fire kill probability of AA gun weapon system[J]. Journal of Gun Launch & Control, 2010(1):1-3.( in Chinese)3 仿真讨论




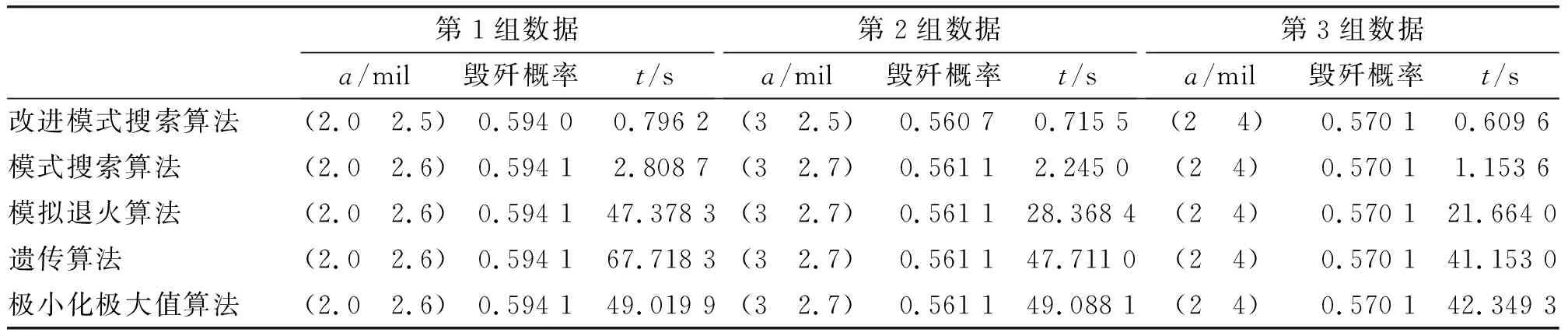
4 结 论

