可变盒子集合投影算子的研究
胡 旭,刘勇进,刘梅娇,高静茹
(1.沈阳航空航天大学 理学院,沈阳 110136;2.沈阳师范大学 教师专业发展学院,沈阳 110034)
本文研究可变盒子集合投影算子的计算方法,即,令(x,t)是IRn×IR空间中给定的向量,我们试图找到(x,t)在可变盒子集合C上投影算子ΠC(x,t)的显示表达式,其中,可变盒子集合C定义如下:
C:={(z,τ)∈IRn×IR:l≤z≤τw}
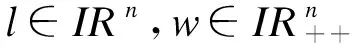
的唯一最优解。
凸锥上投影算子的性质在相关锥约束优化问题理论与算法的研究过程中起着极其重要的作用,如锥约束优化问题的稳定性分析,增广拉格朗日算法的应用与收敛性分析都需要涉及投影算子的性质。基于凸锥上投影算子在锥约束优化问题研究中的重要作用,对各类闭凸集上投影算子的研究引起众多学者的关注和兴趣,并取得了较为丰富的理论研究成果[1-9],在此我们不一一赘述。
对于给定的l,u∈IRn,∀x∈IRn,我们很容易知道盒子约束集合D:={y∈IRn:l≤y≤u}上的投影算子ΠD(x)可以表示为ΠD(x)=min{max{x,l},u},然而,对于可变盒子约束集合C上的投影算子并不是容易计算的,因为C中的τ本身是可变化的。最近,Liu,Wang,Sun[9]给出了如下凸优化问题显示解的计算
s.t.eTy≤τ
0≤y≤τe
其中e是各分量均为的向量。为了研究上述凸二次优化问题的显示解,Liu,Wang,Sun[9]讨论了F:={(y,τ)∈IRn×IR:0≤y≤τe}上投影算子的显示解。本文的目的是给出可变盒子集合C上投影算子显示解的计算方法,容易看出C包含F作为其特殊情形,因此,本文的结果是文[9]相关结果的推广,但是分析难度更大,因为C更为复杂。应当指出的是,由于问题(P)是凸二次优化问题,我们可以通过现有的求解凸二次优化问题的方法和软件对其进行求解,然而,这种方法存在两个明显的缺点,一方面,已有的求解一般凸二次优化问题的方法往往只能求得最优解的近似解;另一方面,已有的求解一般凸二次优化问题的方法计算效率偏低,且不能解决大规模问题。针对以上两个缺点,本文工作的贡献包括以下两方面:其一,通过对优化问题的KKT条件,我们得到了求解C上投影算子显示解的计算方法;其二,本文研究的计算方法能够非常高效的求解大规模问题,具体的数值结果表明,当向量维数达到100万时,只需要1.2秒左右就能得到其显示解。
本文的结构如下:第1节详细讨论了可变盒子集合C上投影算子显示解的计算方法;第2节给出了具体的数值结果,数值结果表明本文研究方法的有效性和高效性;第3节给出了本文的结束语。
1 投影算子的计算方法
在这节中,我们首先给出问题(P)的等价问题(P*),然后根据等价问题的KKT条件,给出问题(P*)最优解的具体形式。
令y=z-l,于是我们可以得到问题(P)的等价问题:
我们很容易知道,如果问题(P*)的最优解为(y*,τ*),那么问题(P)的最优解可以表示为
(z*,τ*)=(y*+l,τ*)
下面我们研究问题(P*)最优解的具体形式。
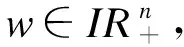
[x/w]π(1)≥[x/w]π(2)≥…≥[x/w]π(n)
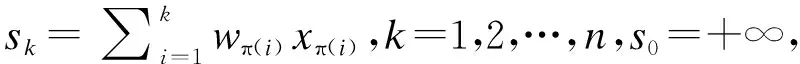
(1)
令
定义:
(2)
以及i=1,2,…,n,
(3)
为了计算在可变盒子上的投影算子,我们在下述定理中给出问题(P*)最优解的刻画,并给出详细的论证。
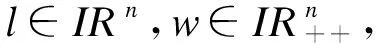
证明:我们分两种情形对本定理的结论加以证明。
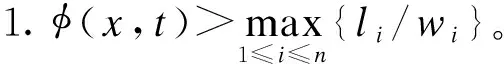
(4)
(5)
下面验证(y*,τ*,u*,v*)满足问题(P*)的KKT条件:
y-x+l-u+v=0
(6)
τ-t-vTw=0
(7)
0≤u⊥y≥0
(8)
0≤v⊥(wτ-l-y)≥0
(9)
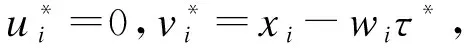
代入(7)后,经简单计算可得,τ*-t-〈v*,w〉=0。因此,(y*,τ*)是问题(P*)的最优解。
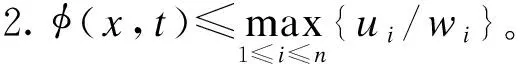
设(y,τ)是问题(P*)的任一可行解,即有0≤y≤τw-l,于是有τ≥τ*。下面证明f(y,τ)≥f(y*,τ*)。为此,我们定义下述指标集
I1(τ):={i:xi≤li},I2(τ):={i:xi≥τwi},I3(τ):={i:li 由于τ≥τ*,我们有 对于任意固定的τ,设y(τ)是下述问题的最优解 s.t. 0≤y≤τw-l (10) 容易知道,y(τ)由下式给出 由于(y,τ)是问题(10)的可行解,所以有f(y(τ),τ)≤f(y,τ)。接下来我们来计算f(y(τ),τ)的最小值。注意到 且 g(τ)≥g(τ*) 依据以上国内外研究现状,本研究认为融入行业英语(EOP)是高职公共英语教学改革的必然,EOP融入后自然会导致原教学生态失衡,提出以生态语言学为指导,改革教学内容、方法、评价及加强师资建设等生态再平衡策略,消除失衡生态中的失调现象及不良影响,使融入EOP的高职公共英语教学生态达到良性平衡。 即 f(y(τ),τ)-f(y*,τ*)≥0 因此有 f(y,τ)-f(y*,τ*)≥0 由于(y,τ)是问题(P*)的任一可行解,所以(y*,τ*)是问题(P*)的最优解。 综合情形1和情形2,根据问题(P*)目标函数的强凸性,我们完成了定理的证明。 根据定理1的结果,以及问题(P*)与问题(P)最优解的关系,对于IRn×IR空间中给定的向量(x,t),我们得到(x,t)在集合C上的投影算子ΠC(x,t)=(z*,τ*),其中 以及i=1,2,…,n, 我们使用Matlab语言对可变盒子集合投影算子的计算进行了有效实现,本节给出计算可变盒子集合投影算子具体算例的数值结果,本节的数值结果是在系统环境为Windows 7、Matlab版本为 7.12的Laptop(双核,CPU 2.8GHz,内存4GB)运行得到的。 下面给出两个例子。例1为给定的四维的具体算例,我们给出其计算详细数值结果,目的是验证我们算法的正确性;例2为随机产生的大规模具体算例,我们给出其计算时间,目的是阐述算法的有效性。 例1假定问题(P)中的x,t,l,w分别为 x=(0.8,0.6,0.3,0.4)T,t=-0.2 l=(0.1,0.1,0.5,0.5)T w=(0.5,0.5,1,1)T 通过对定理1的结果编程,得到ΠC(x,t)=(z*,τ*),其中 z*=(0.25,0.25,0.5,0.5)T,τ=0.5 例2对于给定的n=5000,104,5×104,5×105,116,5×106,107,向量x的每个分量服从[0,1]均匀分布,其Matlab命令:x=rand(n,1):t=-0.001n;向量l,w分别由下列Matlab命令产生: 1=0.3*ones(n,1) w=randi(10,n,1)/10 其中,randi(10,n,1)表示产生1至10范围内的n维随机整数向量。 表1给出了例2的数值结果。表中n表示向量x的维数,对每一个n的情形,我们随机产生10个算例,然后计算其平均时间,表中“s”表示秒。从表1我们可以看出,当n=107时,其计算平均时间约为1.2秒。 表1 例2数值结果 本文研究了可变盒子约束上投影算子显示解的计算方法,并给出了具体算例的数值结果。本文的结果可以应用到相关优化问题的研究中,例如,增广拉格朗日方法,无穷范数约束下的最小二乘问题等。今后我们将继续对投影算子的微分性质及其应用开展深入的研究。 参考文献(References): [1] HELGASON R,KENNINGTON J,LALL H.A polynomially bounded algorithm for a singly constrained quadratic program [J].Mathematical Programming,1980,18(1):338-343. [2] BRUCKER P.An O(n) algorithm for quadratic knapsack problems [J].Operations Research Letters,1984,3(3):163-166. [3] MACULAN N,PAULA G G De.A linear-time median-finding algorithm for projecting a vector on the simplex of [J].Operations Research Letters,1989,8(4):219-222. [4] PARDALOS P M,KOVOOR N.An algorithm for a singly constrained class of quadratic programs subject to upper and lower bounds [J].Mathematical Programming,1990,46(1-3):321-328. [5] MACULAN N,SANTIAGO C P,MACAMBIRA E M,et al.An O(n) algorithm for projecting a vector on the intersection of a hyperplane and a box in [J].Journal of Optimization Theory and Applications,2003,117(3):553-574. [6] KIWIEL K C.Breakpoint searching algorithms for the continuous quadratic knapsack problem [J].Mathematical Programming,2008,112(2):473-491. [7] DING C,SUN D F,TOH K-C.An introduction to a class of matrix cone programming [J].Methematical Programming,2010(12):1-39. [8] WU B,Ding C,SUN D F,et al.On the Moreau-Yoshida regularization of the vector k-norm related function [DB/OL].http://www.optimization-online.org/DB_FILE/2011/03/2978.pdf,下载时间:2013-03-26. [9] LIU Y-J,WANG S Y,SUN J-H.Finding the projection onto the intersection of a closed half-space and a variable box [J].Operations Research Letters,2013,41:259-264. [10] GRANT M,BOYD S.CVX:Matlab software for disciplined convex programming,version 2.0 beta[DB/OL].http://cvxr.com/cvx,下载时间:2012-12-09.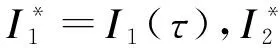
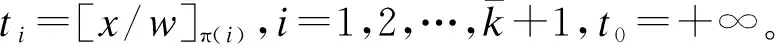
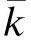
2 数值结果


3 结束语

