基于不同本构关系的夹层梁颤振分析
李国杰,杨晓东
(1.沈阳航空航天大学 航空航天工程学部,沈阳 110136;2.北京工业大学 机电工程学院,北京 100124)
振动普遍存在于各种机械结构中。振动会带来危害,比如降低仪器精度,缩短机械的使用寿命,甚至使机械产生应力疲劳直至破坏。颤振为结构的惯性力、弹性力及结构所受的气动力共同作用下产生的自激振动现象。颤振是一种大幅度的振动,机翼颤振可能会产生严重的飞行事故[1]。
粘弹性材料既具有粘性也有弹性,粘性使其能够吸收振动的能量,从而抑制振动,粘弹性材料广泛应用于结构的振动抑制上。Yang对轴向运动粘弹性梁振动固频及幅频响应做了分析[2],Erickson与Anderson对超声速流中夹层板颤振做了分析[3],Marynowski等对轴向运动夹层梁用Kelvin模型本构关系与Burgers模型本构关系做了对比颤振分析[2],尚没有人研究不同粘弹性模型材料对板结构在气动力下振动的影响,同一结构的粘弹性特性可由不同的本构关系来描述。每一种模型的粘弹性材料的粘性系数、弹性系数也各不相同。如何选择一种合适的粘弹性材料对振动结构的动力学精确描述具有重要意义[4-5]。
对于长宽比较大的矩形板结构,梁模型的计算结果与板模型非常接近[6]。因此,许多细长的工程结构可以简化为梁模型,对梁的振动方面的研究结果能够反映这些结构的振动情况。而且梁理论较为简单,所以本文选择夹层梁作为研究对象,借此反映超声速气流中的细长板结构的动力学行为。首先本文得到简支夹层梁结构模型,对其粘弹性阻尼层分别采用Kelvin模型本构关系与Maxwell模型本构关系。然后对超声速气流带来的气动力采用一阶活塞理论,推导出了夹层梁振动控制方程。最后用Galerkin截断法得到夹层梁振动控制方程的特征值,并对两种粘弹性模型本构关系做了对比分析。
1 夹层梁运动方程
研究对象为超声速气流中的对边简支自由矩形夹层板,本文将其简化为夹层梁,并对其做如下假设[7]:
(1)上下约束层为不具有粘性的各向同性弹性层。阻尼层为各向同性的粘弹性层;
(2)约束层与阻尼层具有相同横向振动位移。约束层与阻尼层之间无相对滑移;
(3)夹层梁为大跨度小厚度梁,约束层与阻尼层均只受纵向应力σx。

图1 超声速流中夹层梁示意图
对夹层梁所受气动力,本文采用一种简化的气动力理论,即一阶活塞理论。研究表明,当马赫数在1.6~5.0之间时[1,12],利用此理论计算得到的气动力可以满足工程上对数值结果精度的要求。
一阶活塞理论的气动力的表达式如下[8-9]:
(1)
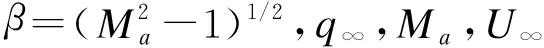
夹层梁的应变与横向振动位移间关系为:
εx=-zw′xx
(2)
夹层梁约束层应力应变间关系为:
(3)
夹层梁阻尼层应力应变间关系为:
(4)
Γ为粘弹性材料特性微分算子。
Kelvin本构关系可以表示为[10],
ΓK=Ej+ηD;
(5)
Maxwell本构关系可以表示为,
(6)

(7)
梁微元横截面所受剪力设为Q,根据梁微元所受力平衡及所受弯矩平衡可得
(8)
(9)
其中
(10)
将应变与横向振动位移关系式(2)、应力与应变关系式(3)及式(4)~(6)代入式(7)可得弯矩Mx。将所求得Mx代入式(8)、式(9)即可分别得到两种粘弹性模型的控制微分方程,如下:

(11)
(12)
其中,H为阻尼层的厚度,h为上下约束层的厚度之和。
2 颤振分析
使用Galerkin法,设横向振动位移为:
(13)
qi(t)=Cieλt
(14)
φi(x)=sin(iπx/L)
(15)
其中φi(x)表示满足简支边界条件的试函数,qi(t)表示位移函数,Ci、λ为常数,L为梁的长度。当夹层梁采用Kelvin模型本构关系,将式(13-15)代入式(11)可得
(16a)
当夹层梁采用Maxwell模型本构关系,将式(13-15)代入式(12)可得
(16b)
对式(16a)、(16b)左右两端乘以φj(x),并在[0,L]之间积分可得到:

(17)
式(17)的解可写为:

(18)
将式(18)代入式(17)得到,
(19)

|λ2M+λC+K|=0
(20)
利用数值方法求解可得特征根λ。表1和2给出了本文采用的梁参数和气动力参数。由这些参数,分别采用Kelvin模型本构关系与Maxwell模型本构关系,通过上述求解方法,得到了马赫数在1.6与5.0之间变化时振动方程的特征根λ。对于流固耦合问题,λ为复数。提取其虚部lm(λ)作纵坐标,马赫数Ma为横坐标,得到图2(a)与图3(a);提取其实部Re(λ)作纵坐标,马赫数Ma为横坐标,得到图2(Vb)与图3(b)。Kelvin 模型运算结果如图2所示,Maxwell模型运算结果如图3所示。

表1 梁模型参数

表2 气动力参数
由图2 (a)及图3 (a)看,随着气流流速的增大,夹层梁第一阶频率逐渐增大,第二阶频率逐渐减小,在马赫数Ma=3.1处发生耦合并产生内共振,共振频率随流速增大而增大。两种粘弹性模型夹层梁的振动频率以及共振点一致。振动频率、共振点受气动力影响,不受所选取的粘弹性模型影响。由图2 (b)及图3 (b)看,气流流速在马赫数Ma=3.1之前,夹层梁第一阶频率、第二阶频率对应的实部重合,随着气流流速的增大,特征根实部从-6.9470减小为-14.0204;气流流速在马赫数Ma=3.1时,前两阶特征值实部分岔为两支,第一阶特征值实部随马赫数增加而递增,在马赫数Ma=3.2处。这说明系统在该马赫数下因颤振而失稳。对比图2 (a)及图3 (a),可知系统在该马赫数下因为内共振不断地出现能量积累,最终发生颤振失稳。

图2 Kelvin模型系统特征根随马赫数变化图
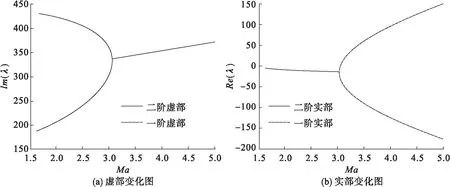
图3 Maxwell模型系统特征根随马赫数变化图

(21)
经数值计算验证,振动方程(21)的求解结果与图2、图3相同。由此可知,对中间层选取不同粘弹性模型对夹层梁的振动频率与夹层梁的振动稳定性不产生影响。
3 结论
本文研究了超声速流中粘弹性夹层梁的稳定性,使用Galerkin离散方法研究了其在超声速气流下的振动情况,主要得到了以下结论:
(1)虽然中间层的不同粘弹性模型会给夹层梁带来刚度上的变化,但中间层粘弹性材料弹性模量不足约束层的1/103,使得Kelvin模型与Maxwell模型下夹层梁中间层均对刚度贡献不足1/106,因此不能影响夹层梁的振动频率及颤振点。则在选取粘弹性材料时可忽略中间层对刚度的影响,选择刚度较大的约束层材料能推迟颤振的发生。
(2)采用Kelvin模型本构关系得到的振动方程中的阻尼项比采用Maxwell模型本构关系得到的振动方程中的略大,高出部分不足1/104,不能对颤振的抑制产生明显区别。
以上分析可知中间层粘弹性模型的选取对夹层梁的振动及颤振影响微小,在选取粘弹性材料时可忽略材料属于哪种模型;选择粘弹性值较大的材料易于提高该系统的稳定性。
参考文献(References):
[1] 杨智春,夏巍,孙浩.高速飞行器壁板颤振的分析模型和分析方法[J].应用力学学报,2006,23(4):527-542.
[2] 杨晓东.轴向运动粘弹性梁横向振动分析[D].上海:上海大学,2004.
[3] Larry L E,Melvin S A.Supersonic flutter of simply supported isotropic sandwich panels [J].NASA TN,D-3171,Langley Research Center,Langley Station,Hampton,VA,1966.
[4] Fei L,Rao M D.Vibration analysis of a multiplelayered viscoelastic structure using the biot damping model [J].AIAA J,2010,48(3):624-644
[5] Rao M D.Recent applications of viscoelastic damping for noise control in automobiles and commercial air planes [J].Journal of Sound and Vibration,2003,262(3):457-474.
[6] Marynowski K,Kapitaniak T.Kelvin-voigt versus burgers internal damping in modeling of axially moving viscoelastic web [J].Int.J Non-Linear Mech,2002,37:1147-1161.
[7] Krzysztof M.Dynamic analysis of an axially moving sandwich beam with viscoelastic core [J].Composite Structures,2012,94:2931-2936.
[8] 肖艳平,杨翊仁,叶献辉.三维粘弹壁板颤振分析[J].振动与冲击,2011,30 (1):82-86.
[9] Gabriel A O.Unified panel flutter theory with viscous damping effects [J].AIAA J,1983,21(5):767-773.
[10] Pourtakdoust S H,Fazelzadeh S H.Chaotic nonlinear viscoelastic panel flutter in supersonic flow [J].Nonlinear Dynamics,2003,32(4):387-404.
[11] 陈安福,杨晓东.超声速气流中平板的颤振分析[J].沈阳航空航天大学学报,2011,28(5):16-17.
[12] 边青峰.夹层壁板颤振复模态方法分析[D].沈阳:沈阳航空航天大学,2012.

