某重型车悬架系统静强度及疲劳耐久性分析
梁江波
(陕西重型汽车有限公司,陕西西安 710200)
平衡轴是悬架系统重要承力部件,在使用中出现局部断裂,为了进一步找出其断裂破坏原因,对悬架系统进行静强度及疲劳分析,静强度分析采用汽车行业功能强大的通用有限元分析软件Hyper-Works,疲劳分析采用FEMFAT5.0.图1、图2为整体式平衡轴断裂后的照片。
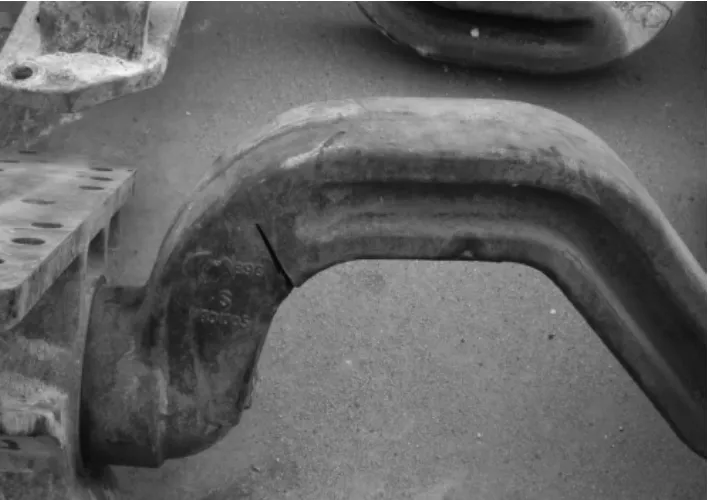
图1 整体式平衡轴断裂状态

图2 整体式平衡轴断裂局部
1 悬架系统分析有限元模型的建立
在 Hyper Mesh11.0中,选择 Radioss(Bulk Data)模板,截取部分车架总成模型,建立包括各相关零件的较为完整的分析计算模型。车架支撑板、纵梁、内衬梁等板件采用二维壳单元,单元尺寸为10 mm;铸造横梁、平衡轴支架、平衡轴采用四面体单元,单元尺寸为6 mm。平衡轴支架通过螺栓连接固定在车架上;考虑平衡轴支架与平衡轴之间有2 mm的间隙,在其接触处采用1 D里面G AP单元进行模拟。图3所示为悬架系统有限元模型。
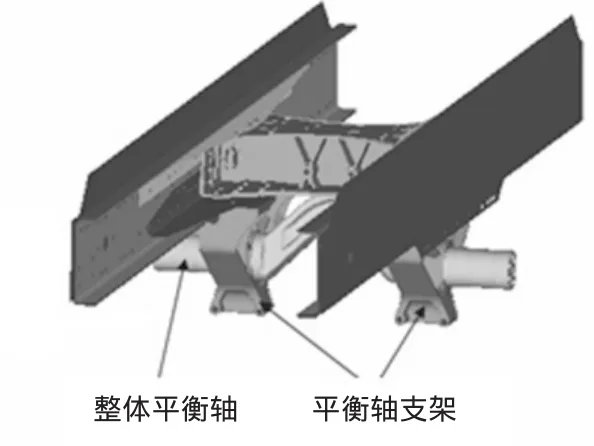
图3 悬架系统有限元模型
2 材料属性和边界条件
悬架系统各部件所对应的材料属性如表1所示。
悬架系统各部件,根据具体的螺栓连接关系,采用Rbe2+Beam进行模拟,在车架前后两端约束全自由度 1,2,3,4,5,6.平衡轴左右两端均布沿 Z 向25t均布力,平衡轴支架下端孔处沿X负方向集中力各3.375 t,重力加速度取g,如图4所示为悬架系统分析有限元模型的约束和荷载示意图。

图4 悬架系统约束和载荷示意图
3 静强度计算结果分析
从计算结果(图5~图8所示)可以看出,平衡轴支架下端处最大位移1.542,平衡轴左端轴线上翘0.207°,右端轴线上翘0.222°.平衡轴支架最大应力为481.2 MPa,安全系数为0.67;平衡轴最大应力284.3 MPa,安全系数为1.13.
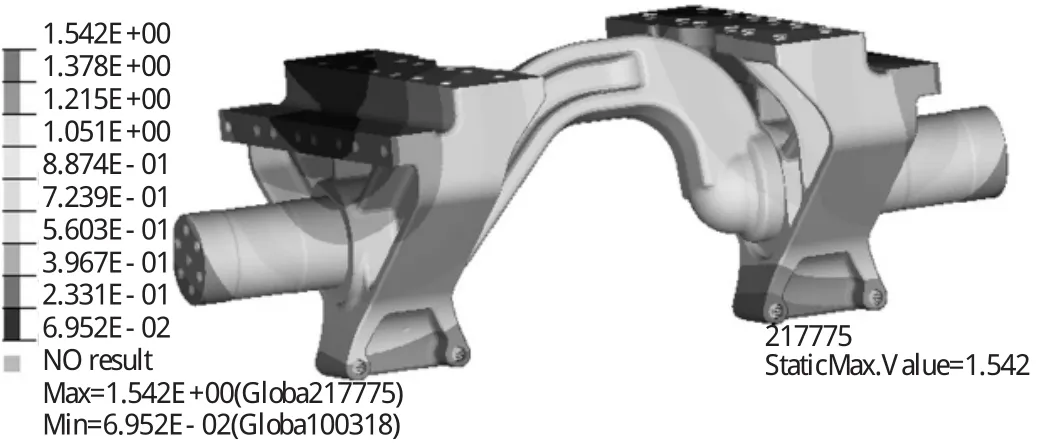
图5 平衡轴位移计算结果

图6 平衡轴轴线上翘量计算
根据实际的工程经验,对于疲劳破坏的钢结构来说,在静力工况下,当应力达到某一极限值时,结构就会发生疲劳破坏,但是,该应力极限一般要比材料的屈服应力值小。该平衡轴所用材料的屈服强度RP是320 MPa,极限拉伸强度σ是500 MPa,根据经验公式,在106次循环破坏时,对应的应力值是250 MPa.对于平衡轴这样重要的部件来说,其重要性非常高,定义这些部件的寿命为106次。如果其结构应力超过该极限值,则有疲劳破坏的危险。
平衡轴疲劳极限大小取为:0.5 σ=250 MPa.由平衡轴应力计算结果知,最大应力及次大应力均超过其疲劳极限250 MPa,有发生疲劳破坏的危险,该位置与实际断裂的位置完全相同。
在FEMFAT5.0中,以悬架系统的应力结果为疲劳应力幅值,计算对称应力循环(即R=-1)时,对悬架系统进行疲劳分析,计算平衡轴支架和平衡轴的最小疲劳安全系数及疲劳寿命,如图9~图12所示。
经过分析,平衡轴、平衡轴支架存在局部应力集中部位,最小安全系数只有0.67;结合疲劳耐久性分析计算,支架最小疲劳安全系数为0.43,疲劳寿命为1.40×102次;平衡轴最小安全系数为1.13,最小疲劳安全系数为0.43,疲劳寿命约5.67×104,低于存活率达到99.9%条件下,零部件安全系数需达到1.32的要求。

表1 材料属性
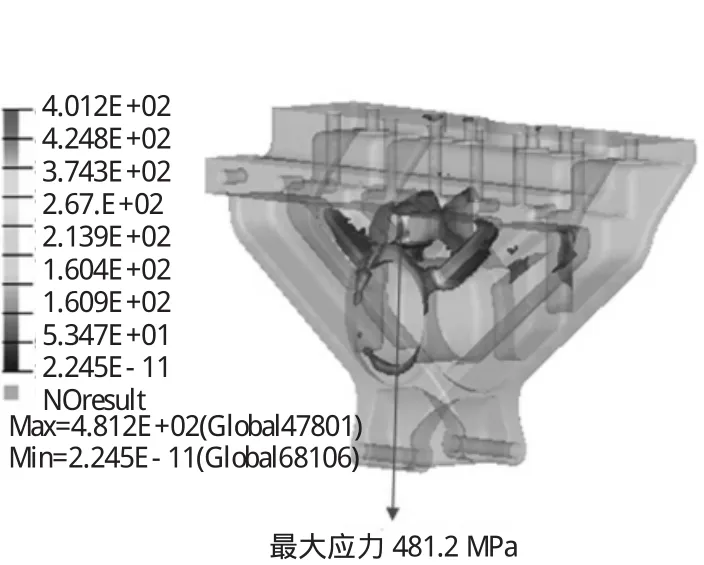
图7 平衡轴支架应力计算结果
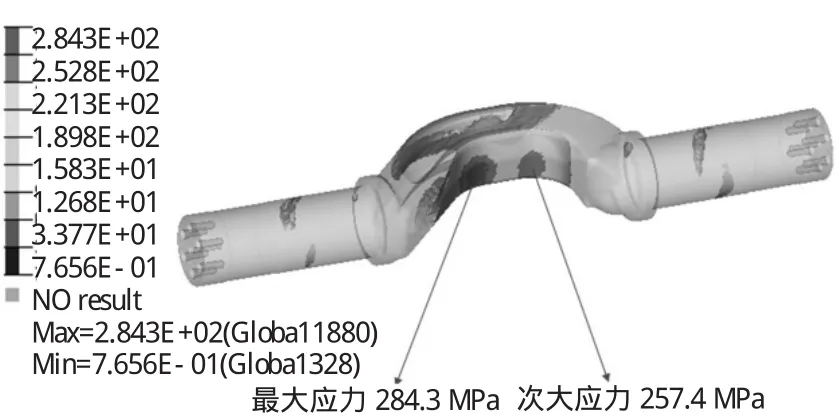
图8 平衡轴应力计算结果
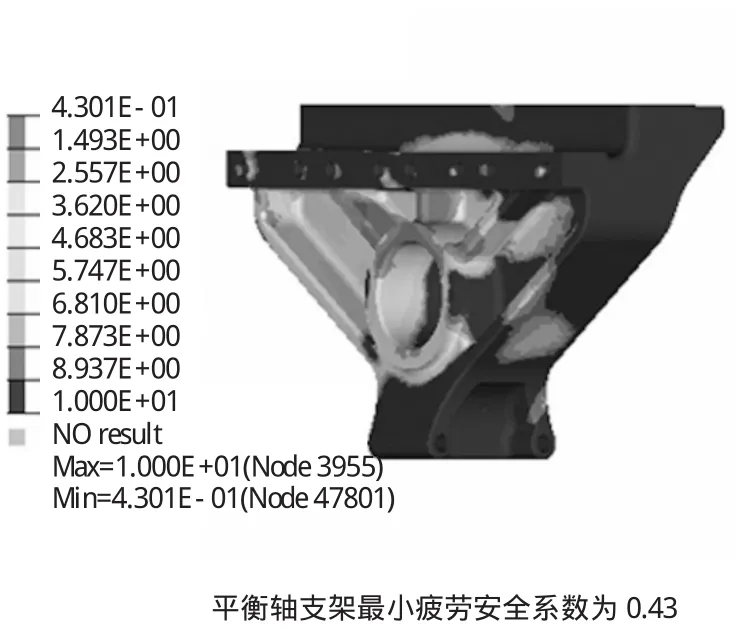
图9 平衡轴支架疲劳安全系数

10 平衡轴疲劳安全系数
由以上分析,我们可以得出结论,市场上出现的平衡轴断裂现象,主要是由于平衡轴所用材料屈服强度和抗拉强度过低,容易产生疲劳破坏所致,可考虑对平衡轴支架及平衡轴更换材料或改进结构,从而提高其强度安全性。

图11 平衡轴支架疲劳寿命
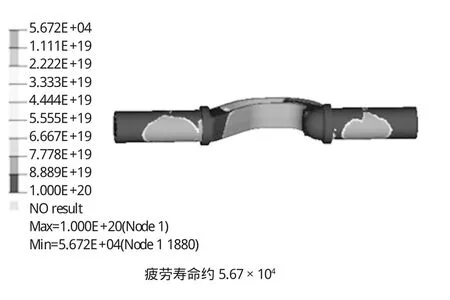
图12 平衡轴疲劳寿命
4 结束语
文章针对某平衡轴支架断裂的具体问题,在Hyper Mesh11.0-Radioss软件环境下建立了悬架系统有限元模型,并对其进行了静强度分析,找到了平衡轴破环的具体原因为疲劳失效引起;在FEMFAT5.0中对该悬架系统进行了对称应力循环下的疲劳耐久性分析,由分析结果,平衡轴不能满足疲劳安全系数的要求。最后对平衡轴提出了建议,为设计优化改进指明了方向。
[1]陈家瑞.汽车构造[M].北京:机械工业出版社,2002.
[2]王望予.汽车设计[M].北京:机械工业出版社,2003.
[3]李楚琳.HyperWorks分析应用实例[M].北京:机械工业出版社,2008.
[4]周中坚,卢耀祖.机械与汽车结构的有限元分析[M].上海:同济大学出版社,1997.
[5]龚培刚.有限元方法及其在汽车工程中的应用[M].重庆:重庆大学出版社,1988.
[6]马文华.弹性塑性有限元[M].湖南:湖南科学技术出版社,1983.

