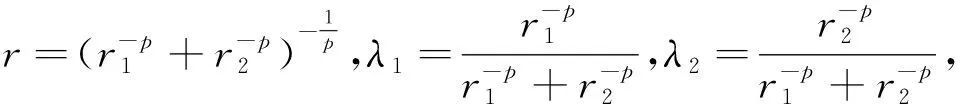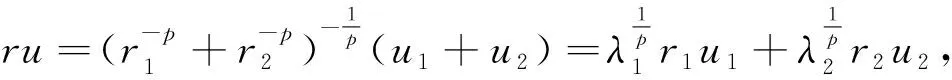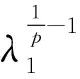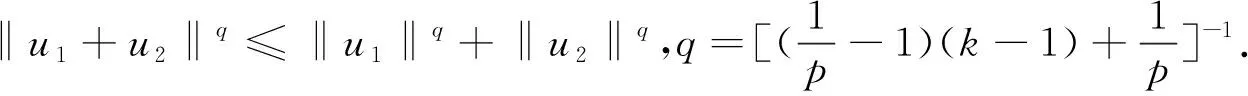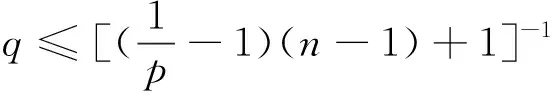相交体的凸性研究及Busemann定理的一点注记
魏超
(西南大学数学与统计学院,重庆 400715)
1 预备知识
本文在Rn(n≥2)中考虑,Sn-1表示n-1维单位球面.
如果一个紧集具有非空内部,我们就称这个紧集为体.定义一个关于原点的星形集K的径向函数:
ρK(u)=max{λ≥0:λu∈K},u∈Sn-1
(1.1)

更进一步地,如果ρK(u)是关于u的正的连续函数,则称K为星体.
将ρK(u)的定义域扩充为Rn{0},我们不难发现ρK(u)是-1阶齐次的,即ρK(λu)=λ-1ρK(u).


(1.2)
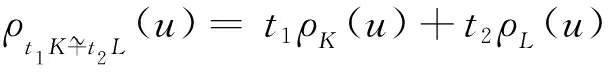
(1.3)

(1.4)
Lutwak[1]首先引入了一个星体K的相交体IK这一概念.IK是通过它本身的径向函数来定义的:
ρIK(u)=|K∩u⊥|,u∈Sn-1
(1.5)
这里,u⊥表示与向量u垂直的超平面,也就是说u⊥={x∈Rn:x·u=0},其中x·u表示Rn中x与u的普通内积.
|A|k=|A|表示集合A的k维Lebesgue测度.对于向量x∈Rn,|x|表示x的模长.
我们关注的是星体K的相交体IK的凸性.这方面的一个重要结果就是经典的Busemann定理[2],叙述如下:
定理1.1[2]设K为Rn中一个关于原点对称的凸体,那么它的相交体IK也是凸的.
Berck[3]最近给出了Busemann定理的一个全新证明.Busemann定理所讨论的对象是凸体,而在实际情况下,我们所遇到的体常常又是非凸的,本文中一个主要目的就是对p-凸体的相交体的凸性作了探讨,并得到一些结果.
Busemann在1953年给出了下列一个定理:
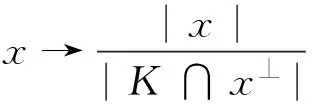
(1.6)
是伴随某体K的Minkowski范数.
这里,我们不难发现:ρIK(u)=|K∩u⊥|=‖u‖-1,因而定理1.2中的范数是定义在IK上的.
A Giannopoulos和V D Milman在2000年又得到了下列一个定理:
定理1.3[5](A Giannopoulos)设K为Rn中的对称凸体,1≤k≤n,E为Rn中的(k-1)维子空间,对任意的z∈E⊥,定义
E(z)=span(z,E)={x+tz:x∈E,t>0}
(1.7)

(1.8)
是一个定义在E⊥上的Minkowski范数.
本文中的另一个结果就是推广了定理1.3并给出了相交体的对偶Brunn-Minkowski不等式.
2 主要结果


命题2.1 当0 命题2.1的证明设K为p1-凸体.根据p-凸体的定义,我们有:当x,y∈K时, 即K是p2-凸体.证毕. 我们自然地会问:如果K是一个对称p-凸体,那么对于某些q而言,K的相交体IK是否必为q-凸体?答案是肯定的,这正是我们得到的第一个重要结果,如下列定理2.2所述: 另外,我们推广了定理1.3,得到了另一种表现形式的Minkowski范数,这是我们得到的第二个重要结果,即下述定理2.3: 定理2.3 设K是Rn中的对称凸体,1≤k≤n,E为Rn中的(k-1)维子空间,对任意的z∈E⊥∩Sn-1,定义 E(z)=span(z,E)={x+tz:x∈E;t>0}, (2.1) 是一个定义在E⊥∩Sn-1上的Minkowski范数. 定理2.3的证明根据Zhang[6]里的内容,我们知道,当考虑一个定义在支持函数上的函数F(hK)=V(K1,…,Kn-1,K)时,利用混合体积的单调性,有下式成立:F(f)≥0,当f≥0 (2.2) (2.3) 根据(2.3)式,我们有 (2.4) 实际上,V(K∩E(z))=|K∩E(z)|k.又有|z|=1,这样,(2.1)式便可写成: (2.5) 根据定理1.3,我们得到:函数(2.1)式是一个定义在E⊥∩Sn-1上的Minkowski范数.证毕. 根据定理2.3,我们有: (2.6) 外部因素主要包括一个企业所处的地域、国家宏观经济发展水平、相关政策与法律法规、高管人才状况、行业部分特点等。其中,在相关政策与法律法规、行业部分特点两条中,国企高管薪酬的体现比较明显,因为这些企业存在垄断、部分垄断或权力支撑等问题,它的经营条件、环境对比非国有企业具有先天优势。事实上,这也是国企高管薪酬备受争议的关键所在。除此之外,在外部环境因素中,关注的焦点仍是薪酬的竞争力。 本文的第三个主要结果就是给出了新意义下相交体的对偶Brunn-Minkowski不等式, 即下述定理: 定理2.4 设K,L是Rn中的对称凸体, 那么 (2.7) 等号成立当且仅当K和L位似. (2.8) 对于u∈Sn-1, 由于 (2.9) 由(1.4)式,有 (2.10) 利用Minkowski积分不等式, 我们有 (2.11) 而我们知道 综合以上各式, 我们可知 (2.12) 根据Minkowski积分不等式, 上式等号成立当且仅当ρK(·)与ρL(·)成比例, 即K与L位似. 引理3.1 设K是Rn中的对称p-凸体,p∈(0,1],1≤k≤n,E为Rn中的(k-1)维子空间.那么函数 引理3.1的证明我们采用文献[7]中的方法加以证明.令u1,u2∈E⊥且u1,u2线性无关.令u=u1+u2,那么 我们通过下列两式定义函数r1=r1(t)和r2=r2(t): 根据Brunn-Minkowski不等式[8],我们有 因此,我们有 因此,ρ(u)唯一确定了一个q-凸体.证毕. 引理3.2的证明我们在引理3.1的前提下来证明该引理.令L=IK为K的相交体.令v1,v2∈span(u1,u2)且分别与u1,u2正交.令E=span(u1,u2)⊥且u1,u2为单位向量,那么 ρL(v1)=|K∩span(u1,E)|=ρ(u1), 且 ρL(v2)=|K∩span(u2,E)|=ρ(u2). 定理2.2的证明结合命题2.1及引理3.2,易知: [1] Lutwak E. Intersection bodies and dual mixed volumes[J]. Adv Math, 1988,71:232-261. [2] Ball K. Logarithmically concave functions and sections of convex sets inn-dimentional Euclidean space[J]. Studia Math, 1988,88:69-84. [3] Berck G. Convexity of Lp-intersection bodies[J]. Adv Math, 2009,222:920-936. [4] Busemann H. Volume in terms of concurrent cross-sections[J]. Pacic J Math, 1953(3):1-12. [5] Giannopoulos A, Milman V D. Extremal problems and isotropic positions of convex bodies[J]. Israel J Math, 2000,117:29-60. [6] Zhang G Y. Convex geometric analysis[M]. Not for Distribution, 2009:33-34. [7] Gardner R J. Geometric Tomography[M], Second edition. Cambridge: Cambridge University Press, 2006. [8] Gardner R J. The Brunn-Minkowski inequality[J]. Bull Amer Math Soc, 2002,39:355-405.



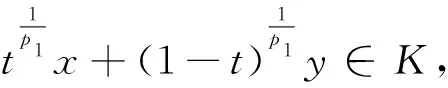



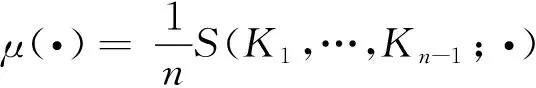

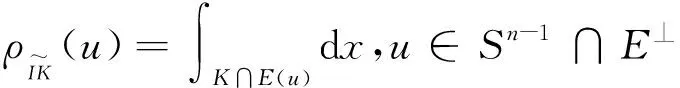


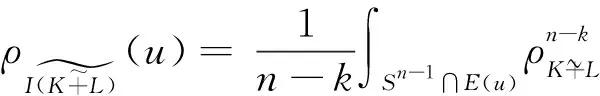
3 定理2.2的证明