一类分数阶热传导方程的Fourier正则化方法

钱爱林，毛剑峰

(湖北科技学院数学与统计学院，湖北 咸宁 437100)

0 引言

近年来，分数阶导数和它的应用引起了许多学者的高度关注，分数阶微分方程已经广泛应用于物理、化学、信号处理、系统识别、生物、电子、金融等领域[1-3].反向热传导问题由t=T时刻的温度确定区间[0,T)上的温度分布，因此又称终值问题.它在航空航天、冶金铸造、化工制药、材料冶金、机械制造、建筑工程、交通运输、核反应堆、地热能勘探、生物传热、土木工程、无损探伤等工程领域具有广阔的应用前景[4-8].分数阶热传导方程通过将标准热传导方程中的一阶时间导数替换成分数阶导数α(0≤α≤1)，它常用于描述漫散射现象，这是一个不适定问题，即Cauchy数据的微小扰动会导致解的失真.对此问题，Murio利用磨光化方法，给出了一个有限差分的空间匹配方案.本文中考虑一维分数阶热传导问题.当需要确定一个物体表面温度分布，但又无法在物体表面进行直接测量，在数学上可描述为如下热方程的Cauchy问题：

这里要用u(1,t)=g(t)来确定在0≤x<1点物理的温度u(x,t).由于实际中g是测量所得，必定有测量误差，假设函数gm∈l2，使得 ‖gm-g‖=‖gm-u(1,·)‖≤ε

(1)

其中常数ε>0表示测量误差,‖·‖表示l2-范数.对x≥1，可将gm作为初始数据在一个四分之一平面内求解一个适定问题；对0≤x<1，有下面的热传导方程

(2)

1 Fourier正则化方法

(3)

对(1)式作Fourier变换，在Fourier空间中有

(4)

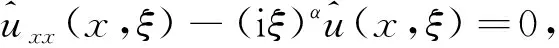
(5)

(6)

由于

(7)

这里xmax是[-ξmax,ξmax]上的特征函数：

(8)

2 误差估计

这一部分将给出正则化解和精确解之间的误差.假设解有一个先验界‖u(0,·)‖≤M，这对讨论不适定问题是必须的，否则，正则化解收敛于精确解的速度可任意慢.由(8)式给出的两个正则化解之间的关系由下面的引理给出.

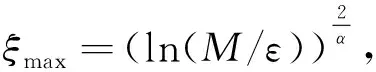
(9)

引理2.1的证明由Parseval等式可得

(10)

(11)

由引理2.1可以得出由(8)式定义的正则化解连续依赖于输入数据.下面给出对应于同样的精确数据g(t)，(6)式定义的精确解和(8)式定义的正则化解之间的误差.

(12)

引理2.2的证明由于当ξ∈[-ξmax,ξmax]时u，v是一致的，由Parseval不等式可得

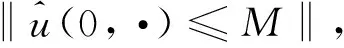
由引理2.1，引理2.2可得

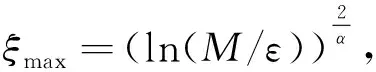
(13)

定理的证明假设v1是由(8)式定义的对应于精确数据g的解，则由三角不等式和引理2.1和引理2.2可得：

(14)

注：从定理可以看出，由(8)式定义的正则化解是精确解的近似，近似误差连续依赖于测量误差.

3 数值算法

(15)

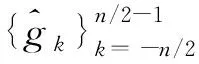
(16)

其中F是Fourier矩阵[9]，Λ是对应于三角插值微分的对角矩阵，这样Λ的对角元素是

其中|ξk|如(15)式所表示.F和一个向量的乘积可通过快速Fourier变换计算，这样就得到了一个计算正则化解(8)式的有效方法.当利用快速Fourier变换计算时要求Gm表示一个周期函数.至于怎样将一个函数周期化请参考文献[10].

[1] Scalas E, Gorenflo R, Mainardi F.Fractional calculus and continous-time finance[J]. J Appl Phys, 2000,284:376-384.

[2] Podlubny I. Fraction differencial equations[M]. San Diegol： Academic Press, 1999.

[3] Metzler R， Klafter J.The random walk guide to anomalous diffusion: a fractional dynamics approach[J].Phy Rep, 2000,339:1-77.

[4] Tikhnov A N， Arsenin V Y.Solutions of ill-posed problem[M]. Washington： Winston and Sons, 1977.

[5] Guo L D A.A modified space-marching finite-difference algorithm for two-dimensional inverse heat condution problem with slab symmetry[J]. Inverse Problem, 1991(7):247-259.

[6] 邢家省，王洪志，张愿章.连续初值条件下热传导方程古典解的存在性证明[J].河南：河南科学，2010(3)：7-10.

[7] Jourhmane M， Mera N S.An iterative algorithm for the backward heat conduction problem based on variable relaxtion factors[J]. Inverse Problems in Engneering, 2002(10):93-308.

[8] Han H, Ingham D B, Yuan Y. The boundary element method for the solution of the backward heat conduction equation[J]. J Comp Phy, 1995,116:292-329.

[9]Van C F.Computational frameworks for the fast Fourier transform[M]. Phiadephia：SIAM,1992.

[10] Elden L,Berntssion F, Reginska T.Wavelet and Fourier methods for solving the sideways heat equation[J].SIAM J Sci comput,2000,21(6):2187-2205.