受限于凸函数的两类解析函数族

熊良鹏，田琳，刘晓丽

(成都理工大学工程技术学院，四川 乐山 614007)

0 预备知识

S表示在单位开圆盘Δ={z:|z|<1}内解析的函数族，其包容的函数形式为

f(z)=z+a2z2+a3z3+…+anzn+…，z∈Δ,

S*和κ分别代表通常意义的星形函数族和凸函数族，都是S的重要子类.

若对于两个函数g(z)，G(z)∈S，存在Δ内解析的函数ω(z)满足ω(0)=0,|ω(z)|<1，使得g(z)=G(ω(z))成立，则称g(z)从属于G(z)，记为g(z)G(z).一个函数f(z)定义为被另外一个函数g(z)在Δ内优化，当且仅当存在Δ内的解析函数φ(z)满足|φ(z)|<1，使得f(z)=g(z)φ(z)，z∈Δ,记为g(z)≪G(z).现在设

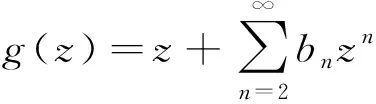
定义0.1 如果函数f(z)∈ψa当且仅当f(z)∈S且满足下面不等式

(1)

Peng Z G[3], Mehork B S等[4]和熊良鹏[5-6]等曾用各种途径解决过相关结构模式函数族的系数估计及其他问题.

定义0.2 如果函数f(z)∈Hψa当且仅当f(z)∈S且存在函数λ(z)∈ψa使得f(z)满足如下的非同构Cauchy-Euler微分方程

本文中得到ψa和Hψa的全部系数估计结果.

1 主要结果

引理1.1[7]如果f(z)=z+a2z2+a3z3+…+anzn+…∈κ，则|an|≤1，n≥2.

引理1.2[8]如果函数f(z)在Δ内解析且满足f(0)=0,|f(z)|<1，则在Δ内恒有|f(z)|<|z|且f(z)=zω(z)成立，这里ω(z)=c0+c1z+c2z2+…+cnzn+…在Δ内解析，且|ω(z)|<1.

定理1.1 如果函数f(z)=z+a2z2+…+anzn+…∈ψa，则当n≥2时有

定理1.1的证明f(z)∈ψa，则由(1)式，有

(2)

则F(0)=0,|F(z)|<1，且F(z)在Δ内解析.再由引理1.2有|F(z)|≤|z|,且F(z)=zω(z)，这里ω(z)=c0+c1z+c2z2+…+cnzn+…在Δ内解析，且|ω(z)|<1.

(3)

因为g(z)∈κ，则由文献[7]有G(z)=zg′(z)∈S*，所以G(z)在单位圆盘Δ内是单叶的.下设

(4)

由(3)式及文献[9]知，则|tn|≤n成立.(2)式经简单计算有

(5)

再由文献[10]有|rn|≤y1=1+a.进一步地，由(5)式可推理

(6)

所以(4)式确保了(zf′(z))′-g′(z)=M(z)T(z)，将等式两边幂级数展开，对比zn-1项的系数得

n2an-nbn=(1+a)tn-1+ar1tn-2+ar2tn-3+…+arn-2t1，

即

n2an=(1+a)tn-1+ar1tn-2+ar2tn-3+…+arn-2t1+nbn

(7)

由于g(z)∈κ，由引理1.1有|bn|≤1，又|tn|≤n，|rn|≤1+a.因此(7)式确保

n2|an|=|(1+a)tn-1+ar1tn-2+…+arn-2t1+nbn|≤

(1+a)|tn-1|+a|r1||tn-2|+…+a|rn-2||t1|+n|bn|≤

(1+a)(n-1)+a(1+a)[(n-2)+(n-3)+…+1]+n=

特别地，若在定理1.1中分别取a=0和a=1，可以得到下面两个推论.

推论1.1 如果函数f(z)=z+a2z2+…+anzn+…∈ψ0，则当n≥2时有

推论1.2 如果函数f(z)=z+a2z2+…+anzn+…∈ψ1，则当n≥2时有

定理1.2 如果存在函数λ(z)=z+λ2z2+…+λnzn+…∈ψa按照定义0.2满足非同构Cauchy-Euler微分方程且使得f(z)=z+a2z2+a3z3+…+anzn+…∈Hψa，则有

定理1.2的证明因为λ(z),f(z)满足非同构Cauchy-Euler微分方程，则依据定义0.2简单推理有

这里n∈N且n≥2,μ∈R(-∞,-1].

再由定理1.1，则容易看出

证毕.

本文中定理1.1和定理1.2分别得到了关于ψa和Hψa的函数的全部系数估计结果，但是这个结果的界不是最好的，如何找到ψa和Hψa两函数族精确的系数估计需要做更深入的讨论.

[1] Goel R M, Sohi N S. On certain classes of analytic functions[J].Indian J Pure Appl Math, 1980,11(10):1308-1324.

[2] Altintas O. A subclass of analytic functions[J]. Yokohama Mathematical Journal, 1987,35:71-73.

[3] Peng Z G. On a subclass of close-to-convex functions[J]. Acta Mathematica Scientia, 2010,30B:1449-1456.

[4] Mehork B S, Singh G. A subclass of close-to-convex function[J]. Int Journal of Math Analysis, 2010(4):1319-1327.

[5] 熊良鹏.一类新的近于凸函数子集[J].湖北大学学报：自然科学版，2010，32(1)：13-17.

[6] 熊良鹏，刘晓丽.两类复序解析函数的系数估计[J].五邑大学学报：自然科学版，2011，25(1)：16-19.

[7] Hallenbeck D J, Macgregor T H. Linear problem and convexity techniques in geometric function theorey[M]. New York: Putnam Publishing Group, 1984.

[8] 钟玉泉.复变函数论[M].北京：高等教育出版社，2004.

[9] Macgregor T H. Majorization by univalent functions[J]. Duke Math J, 1967,34:95-102.

[10] Xu Q H, Gui Y C, Srivastava H M. Coefficient estimates for certain subclasses of analytic functions of complex order[J]. Taiwanese Journal of Mathematics, 2011,15(5):2377-2386.