Bézier曲面的降多阶最佳逼近

植 物，白根柱，包德喜

(内蒙古民族大学 数学学院，内蒙古 通辽 028043)

近年来，曲面的降阶方法主要集中在曲线方面，对高次多项式曲面，大多数都应用曲线降阶方法的推广[1-2]，另外文献[3-4]也给出了曲面的降阶方法.在上述高次多项式曲面的降阶方法中，文献[5]提出的方法要求角点高阶插值.而其他降阶方法一般都不能保证角点高阶插值，这不仅与几何造型系统的迫切要求是不相适应的，而且对误差范围相对要大的.文献[6]给出了张量积Bézier曲面的S幂基降多阶逼近方法，本文在此基础上给出了一种新的降阶方法，该方法主要基于S幂基的角点高阶插值和对称性,所得到的降阶曲面的误差要低.本文的分向降阶方法有别于文献[6]提出的Bézier曲面的降阶方法，该方法采用不同方向的每一个Bernstein基函由低阶的S幂基的线性组合去最佳逼近,再由张量积的定义就可得到一次降多阶的逼近曲面.

1 Bézier曲面的降多阶最佳逼近方法

下面采用了分向降阶方法，对u向，w向的每个Bernstein基函数由二范数意义下可以找到逼近元.以低阶S幂基函数的线性组合去逼近给定的Bernstein基函数.首先在每个方向上构造线性空间.其次，在该线性空间上定义二范数,在二范数意义下构成banach空间.最后，求出最佳逼近元.

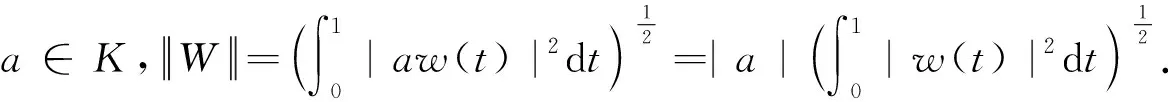
定理1[8]设为赋范空间X的有穷维子空间，则对于每一个x∈X必存在M中对x的最佳逼近.

定理2[8]设是严格凸的赋范空间，已知子空间M⊂X，则M中对每个给定的x∈X的最佳逼近至多有一个.

当n,m≥2p时，S幂基函数[7]满足:

对u向，w向的每个Bernstein基函数由以下形式求出最佳逼近元：

i=0,1,…,ni=0,1,…,n

2 误差估计及数值实例

下面定义误差函数为：

图1 9×9张量积Bézier曲面 图2 7×7 降阶逼近曲面 图3 7×7 降阶最佳逼近曲面

图1所示为一张9×9张量积Bézier曲面，图2 所示为文献[6]一次降2×2阶,图3所示为本文方法一次2×2阶，图4所示为文献[6]得到的误差函数的图形，图5 所示为本文方法得到的误差函数的图形.

图4 误差函数的图形 图5 误差函数的图形Fig.4 The graphic of error function Fig.5 The graphic of error function

3 结论

通过图形4和图形5可以看出本文的降阶方法优越于文献[6]提出的方法.还可知道本文方法得到的误差为e=0.001 289 257 781和文献[6]方法的误差为e=1.272 821 707.本文的降阶方法简单和直观，可以一次降多阶.今后将进一步考虑逼近函数的其他形式以及逼近尺度.

参考文献:

[1] Danneberg L，Nowacki H．Approximate conversion of surface representations with polynomial bases[J]．Computer Aided Geometric Design，1985，2(2)：123-131.

[2] Hoschek J．Approximate conversion of spline curves[J]．Computer Aided Geometric Design，1987，4(1)：59-66.

[3] 周登文，刘芳．局涛．张量积Bézier曲面降阶通近的新方法[J]．计算机辅助没计与图形学学报，2002，14(6)：553-556.

[4] Chen G D，Wang G J．Multi-degree reduction of tensor product Bézier surfaces with conditions of comers interpolations[J]．Science In China(Series F)，2002，45(1)：51-57.

[5] 郭清伟，朱功勤．张量积Bézier曲面降阶逼近的新方法[J]．计算机辅助设计与图形学学报,2004，16(6)：777-782.

[6] 张莉，刘植.张量积Bézier曲面的S幂基降多阶[J].合肥工业大学学报：自然科学版,2008,31(10):1710-1713.

[7] Sdnehez-Reyes J．The synmletric analogue of the polynomiai power basis[J]．A CM Trartsactions 013．Graphies，1997，16(3)：319-357.

[8] 王长清.近代解析应用数学基础[M].西安:西安电子科技大学出版社,2001.