城市景观格局的空间尺度效应——以上海市为例

陈命男，郑磊夫

（上海勘测设计研究院，上海200434）

1 引言

近20年来，城市景观格局及其变化已逐渐成为城市生态学研究的热点［1～3］，而景观格局的尺度和尺度效应已经成为其研究的核心问题之一［4，5］。邬建国［6］和Lam［7］等认为，尺度主要是指空间和时间上的粒度和幅度。空间粒度指空间最小可辨单元所代表的特征长度、面积或体积；时间粒度指某一现象或事件发生的（或取样的）频率或时间间隔。幅度是指研究对象在空间和时间上的持续范围［8，9］。

可见，空间尺度包括粒度和幅度两个方面。客观存在的景观空间异质性依赖于空间尺度，当景观空间尺度发生变化时，所量测到的空间异质性也随之变化，因此尺度对景观空间异质性的测量与理解有着重要影响。空间异质性因粒度而异可称为粒度效应，因幅度而异可称为幅度效应。

目前，国内外围绕尺度效应也展开了一定的研究［10～12］，李秀珍等以模拟景观为研究对象探讨了10个景观指标的空间粒度效应［13］；赵文武等和申卫军等以真实景观分析了多种景观生态指数对粒度变化的敏感性，探讨一定比例尺下不同景观生态指数的适宜粒度范围及景观指数随空间粒度变化的临界现象［14］；Wu等以4种真实景观为对象，在较宽的粒度范围和幅度范围上分析了较多的指数，揭示了一些常用景观指数的尺度效应关系［15，16］；Harbin Li等从空间幅度和粒度两方面分析了大量景观指标的适用性和潜在问题，并提出了相应的解决方法［17］。徐建华、岳文泽等以上海市中心城区为例，对城市景观格局空间自相关的尺度依赖性、不同幅度下城市景观多样性的空间分布格局进行了分析，并进一步利用半变异函数对其空间异质性进行定量描述［18］。但从总体上说，城市景观的尺度效应还需要进一步探索和更多的实证研究，尤其是对于如何选择或确定研究城市尺度景观格局演化的合适粒度和幅度尚缺乏系统的研究。

本文以上海市陆域范围为研究区域，从空间粒度方面探讨了20种景观生态指标对粒度的敏感性及其随粒度变化的规律；利用Moran＇s I指数对不同粒度下景观生态格局的空间自相关性进行分析。在此基础上，利用半变异函数探讨这些景观生态指标的空间异质性与幅度的效应关系，揭示景观空间异质性的尺度依赖性，为选择适合于上海城市景观格局演化研究的粒度和幅度提供参考。

2 数据来源与研究方法

2.1 研究区域

上海地处长江三角洲前缘，北界长江，东濒东海，南临杭州湾，西接江苏、浙江两省。本研究区域为上海陆域范围，不包括崇明、长兴和横沙三岛（图1），面积约5155km2。据《上海市统计年鉴》，1979～2006年期间，尤其是1992年以后，上海经济迅速增长，大量耕地、林地等迅速转化为城镇建设用地，整个城市空间迅猛扩展。

图1 研究区范围和地理位置

2.2 数据源

采用2004年7月19日的Landsat－5TM影像作为主信息源，通过几何校正配准至1︰25万地形图，通过横轴墨卡托投影转换至北京54坐标的平面坐标系统下，中央经线123°E。

利用ERDAS IMAGINE 8.6中的Mosaic Image命令完成遥感影像的拼接，并利用图像掩膜模块（Mask）根据上海市的行政区划图在遥感影像上提取出相应的研究区域。通过相关矩阵法选出TM3、4、5波段进行假彩色合成。

考虑到上海土地资源的经营特点、利用方式、覆盖特征等实际情况，根据文献［19］给出的土地资源分类系统，将研究区的土地利用类型划分为耕地、林地、水域、草地、城镇建设用地、未利用地共6大类。采用基于监督分类的人机交互解译方法，在解译过程中，参考了上海市2000年土地利用图（1︰10万）和2003年航空遥感解译的土地利用图（1︰2000）。

为评价分类结果，在研究区内随机抽取256个样点，利用 ERDAS 8.6中的精度评价（Accuracy Assessment）模块，计算2004年各土地利用类型的Kappa指数和总的分类精度（表1），检验结果表明，均达到最低允许的判别精度0.7的要求，可满足本文研究的需要。

表1 土地利用分类结果精度评价（Kappa指数）

2.3 研究方法

2.3.1 景观格局的表征方法

（1）景观生态指标的选择。随着对景观生态格局研究的深入，景观生态指数的数量和复杂程度不断增加，目前经常用到的指数大约有60个［20～22］。然而，并不是所有指标都能很好反应景观格局的变化，在众多的指数之间，往往产生大量的信息冗余，而且有些指标的生态学意义并不明确，甚至互相矛盾［14］。结合本研究区域的特点及空间尺度，本文选择了20个既对景观结构变化敏感又能较全面反映景观格局特征的指标，运用Fragstate3.3定量化地研究上海城市景观格局的尺度效应，其中10个指标用于描述斑块类型层次的景观格局，10个指标用于描述景观层次的景观格局。各指数的计算方法详见文献［1，3］和Fragstate3.3的技术文档。

（2）空间统计指标的选择。景观格局的尺度特征主要表现为对尺度的依赖性。在选择空间统计指标时，主要选择衡量空间关系的两个指标：空间自相关指标Moran＇s I指数和半变异函数［4，15］。 前者的计算公式为［23］：

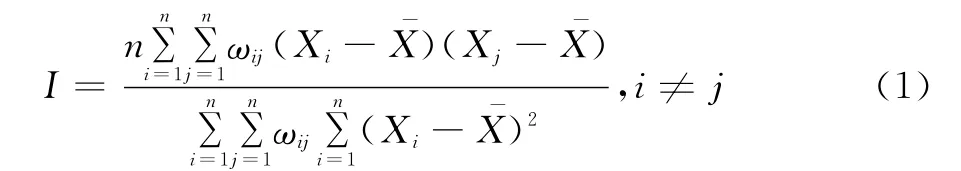
式中：Xi和Xj分别是变量X在配对空间单元i和j上的取值，是变量X的平均值，Wij是相邻权重，n是空间单元总数。

空间自相关系数计算完成后，需要根据计算结果对"变量在所讨论空间呈随机分布（即不存在空间自相关关系）"的原假设进行显著性检验。本研究采用"近似正态法"进行检验。即以近似正态分布为前提，对Moran＇sI指数的计算结果进行标准化，得到衍生统计量z。取双侧检验显著性水平为10%，查表得临界值为±1.65。然后比较z与临界值的相对大小，当z大于1.65时为显著空间正自相关；当z小于－1.65时为显著的负相关［24］。

半变异函数的计算公式为［25］：

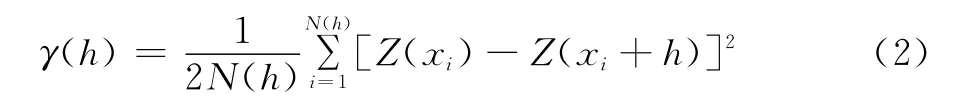
式中：h为两样本点的空间分隔距离，Z（xi）与Z（xi＋h）分别是样本在空间位置xi和xi＋h上的观测值（i＝1，2，…，N（h）），N（h）是分隔距离为h时的样本对总数。

2.3.2 尺度推绎方法

（1）粒度推绎方法。采用粒度上推方法，即将精微尺度上的结果外推到较大尺度，它是研究成果的“粗粒化”。本文采用基于“多数原则”的空间聚合，在ARC/INFO的Resample模块下，采用双线性内插法，对分辨率为30m的景观格局图进行重采样，将栅格图的粒度上推至 60m，90m，120m，150m，180m，270m，300m，360m，420m，这样得到10个不同分辨率的景观格局栅格图层。在ArcGIS9.1中利用Spatial Statistics工具中的空间自相关模型（Spatial Autocorrelation）计算Moran＇s I指数，进一步分析 Moran＇s I指数随分辨率变化的粒度效应。

（2）幅度推绎方法。采用网格化的幅度推绎方法，即在一定的粒度下，利用不同大小幅度的正方形网格（如1km×1km，2km×2km，3km×3km…）覆盖整个研究区域，将其划分为若干数量的子区域，每个子区域就是该空间幅度下的一个统计样方。在不同幅度下，利用半变异函数分析其景观格局的空间异质性。这样不但能分析单个网格内的景观格局，还可以揭示景观指数在所有网格之间的异质性。

3 结果与讨论

3.1 景观生态指数的粒度效应

3.1.1 对粒度变化的响应

图2显示了斑块类型层次上景观指数随空间粒度的变化。

从图2可见，这10个斑块类型层次的景观生态指数随粒度增加呈现出3种变化趋势：①指数值随空间粒度的增大而减小，包括斑块密度（PD）、边缘密度（ED）、面积加权平均形状指数（AWMSI）、面积加权平均分维数（AWMFD）、斑块聚集度指数（AI）；②指数值随空间粒度的变粗而增加，包括平均斑块面积（MPS）、功能性平均最近邻体距离（FNN＿MN）；③指数值几乎没有变化，或存在无规律变化，包括相对丰度（PLAND）、最大斑块指数（LPI）、景观分离度指数（DIVISION）。

PD的空间粒度曲线呈明显下降趋势，并大多在120～150m左右出现尺度转折点，粒度超过180m以后，各斑块类型PD值的差异明显减小。PD值愈大，破碎化程度愈大，一般情况下空间异质性程度也愈大。从图2可见，草地、林地的PD值相对较大，表明这两种斑块的破碎度相对较大。在上海陆域范围，大部分草地和林地均属于城市绿地，因此分布相对较分散，破碎化程度较大。而对于建筑用地，在上海城市化进程中，大量建筑用地分布日趋集中，表现为成片组团式分布，因此建筑用地的PD值小于草地、林地。

ED的空间粒度曲线也大多呈下降趋势，但尺度转折点不明显。MPS的空间粒度曲线则大多呈现上升趋势，农田和建筑用地斑块的MPS大致在180m附近出现尺度转折点。由于粒度增大所产生的“吞噬”效应，使斑块边界、面积出现融合现象，从而改变了ED和MPS值的大小。ED也可在一定程度上反映景观的破碎化程度，粒度增大时，小斑块被融入大斑块，使ED值下降，景观的破碎化程度降低；同时MPS也由于"吞噬"效应而呈现上升趋势，各斑块类型之间MPS值的差异也随着粒度的增大而增加，尤其是农田和建筑用地斑块表现更为显著。

在上海陆域范围，农田和建筑用地斑块是优势斑块，其AWMSI的空间粒度曲线呈明显下降趋势，并在120m附近出现尺度转折点。其他斑块的AWMSI值也有下降趋势，但变化不显著。AWMSI可以反映景观中各斑块的变异性，随着粒度的增加，AWMSI值相应减小，表明随着粒度的增加，各斑块的空间变异性也相应降低。

AWMFD通常从自相似性角度来衡量景观要素镶嵌结构的复杂性。分维数的理论值范围在1～2之间，值越大则斑块形态越复杂。对于某一斑块类型，随着粒度增加，由于“吞噬”效应，该类斑块的面积和周长都将减小，但面积减小的速度更快，从而使其分维数减小，在空间上即表现为斑块形状趋于规则。总体而言，各类斑块的分维数均随粒度变化呈近似线性下降；在粒度较大时，各类斑块的分维数差异减小。一般认为，如果分维数在某一尺度域上不变，那么该景观在这一尺度范围可能具有结构的自相似性［26］。但在本次研究的尺度域上，各类斑块的分维数对尺度的依赖性没有统一的规律，但在粒度较小时，各类斑块的分维数差异较大，随着粒度的增大，差异有减小的趋势。一般认为，人类干扰形成的斑块形状比较规则，相似程度较高，但在上海地区，事实上几乎各类斑块都受到人类活动的强烈影响，建筑用地、农田、林地等斑块在土地资源非常有限并且各用地类型相互转换的复杂背景下形成发展，因此形态较为复杂。

AI的空间粒度曲线随粒度的增大总体呈下降趋势，大多在90～120m附近出现尺度转折点，在30～90m粒度范围内下降趋势明显，而当粒度超过120m后指数变化趋于平稳。AI值可以反映景观中不同斑块类型的非随机性或聚集程度，由于AI考虑斑块之间的相邻关系，还可以反映景观组分的空间配置特征。由于粒度增大所产生的“吞噬”效应，导致斑块间的相邻距离增大，聚集程度降低。

FNN＿MN的空间粒度曲线随粒度的增大总体呈现上升趋势，但不存在明显的尺度转折点。各类斑块的尺度响应曲线也有差异，对于自然景观（如水域）的FNN＿MN，其空间粒度曲线呈近似直线上升，而对于人为景观（如建筑用地和草地等）的空间粒度曲线近似呈折线上升，且这些斑块的粒度曲线呈现出明显的相似性。

PLAND取决于景观中的斑块类型，斑块类型不变，PLAND值虽然会因总面积的轻微变化而发生变化，但因为其变化值过小，而呈现出指数值基本不变的现象。因而，该指数的粒度效应不明显。

LPI的空间粒度曲线总体上较为平稳，林地、绿地、水域和未利用地等斑块的LPI值随着粒度的增大几乎没有变化，但对于优势斑块，如农田和建筑用地斑块，LPI随着粒度的增大缓慢上升，粒度效应关系不明显，也不存在明显的尺度转折点。LPI可以反映景观范围内占主导地位的斑块，随着粒度的增加，由于“吞噬”效应，会导致优势斑块的主导地位更强，表现为优势斑块的LPI值随粒度增加有所增大，当粒度足够大时，非优势类型有可能从景观中完全消失；而优势斑块在粒度增加的过程中既不断地“吞并”其他类型，又有可能不断地被其他类型所“吞并”，基本保持一种动态的平衡。

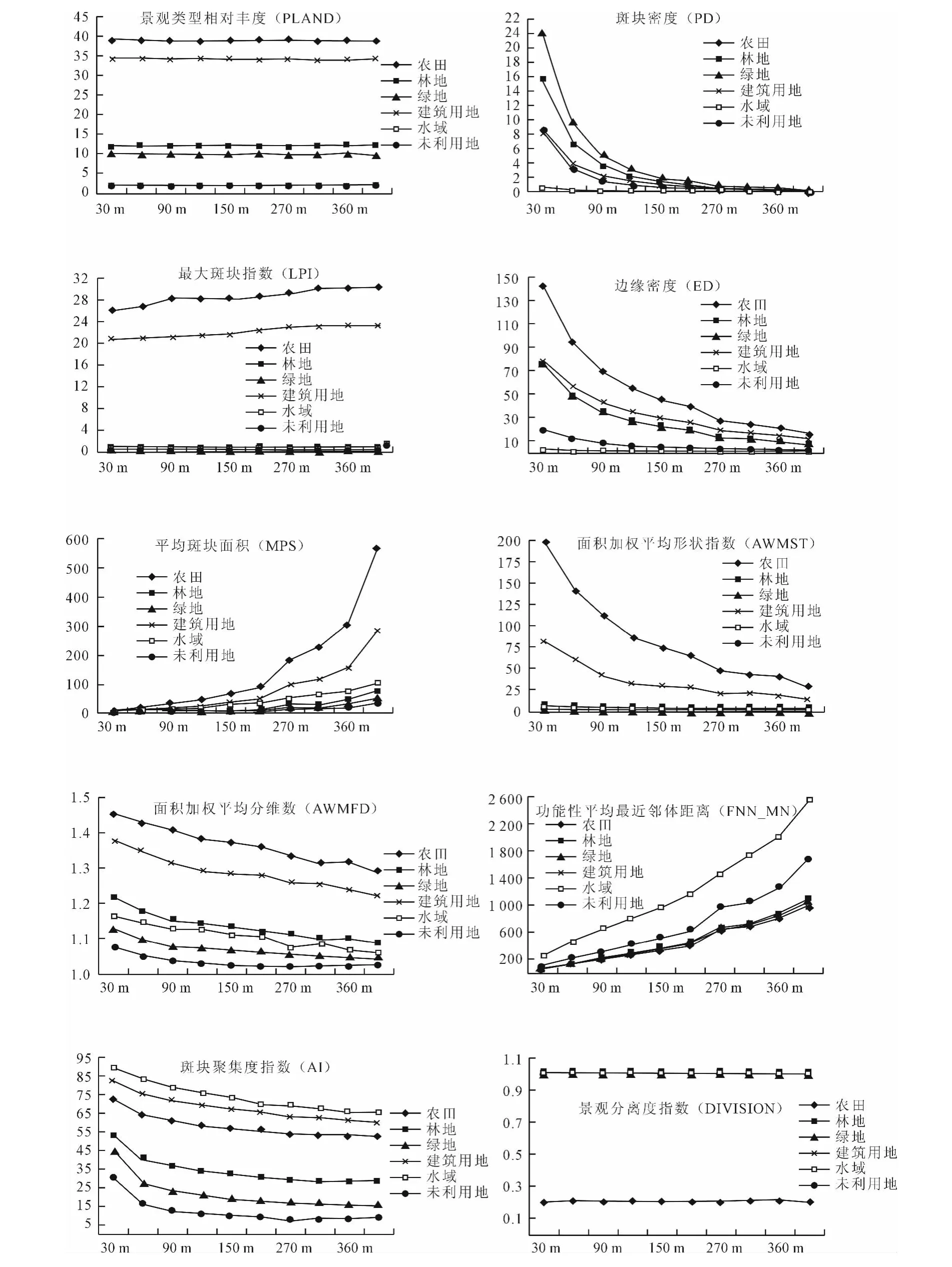
图2 斑块类型层次上景观指数随空间粒度的变化

在景观层次，本文所选用的10个指标对粒度的变化都表现出很强的敏感性，具有明显的粒度效应（图3）。它们随粒度增加呈现出4种变化趋势：①指数值随粒度的增大而减小，具有较明确的粒度效应关系，可预测性较强，且在150m附近存在较明显的尺度拐点。这类指数包括PD、ED、AWMSI和景观聚集度指数（CONT）；②指数值随粒度的增大将最终下降，但尺度转折点不明显，或粒度效应曲线较复杂，可预测性不强，包括AWMFD、景观破碎化指数（SPILT）、Shannon多样性指数（SHDI）；③指数值随粒度的变粗而增加，粒度效应关系与景观格局特征明显相关，具有一定的可预测性，存在较明显的尺度拐点，这类指数包括MPS，它在120～180m之间出现尺度转折；④指数值随粒度的增大将最终上升，但尺度转折点不明显或粒度效应曲线较复杂，可预测性不强。这类指数包括FNN＿MN和景观均匀度指数（SHEI）。

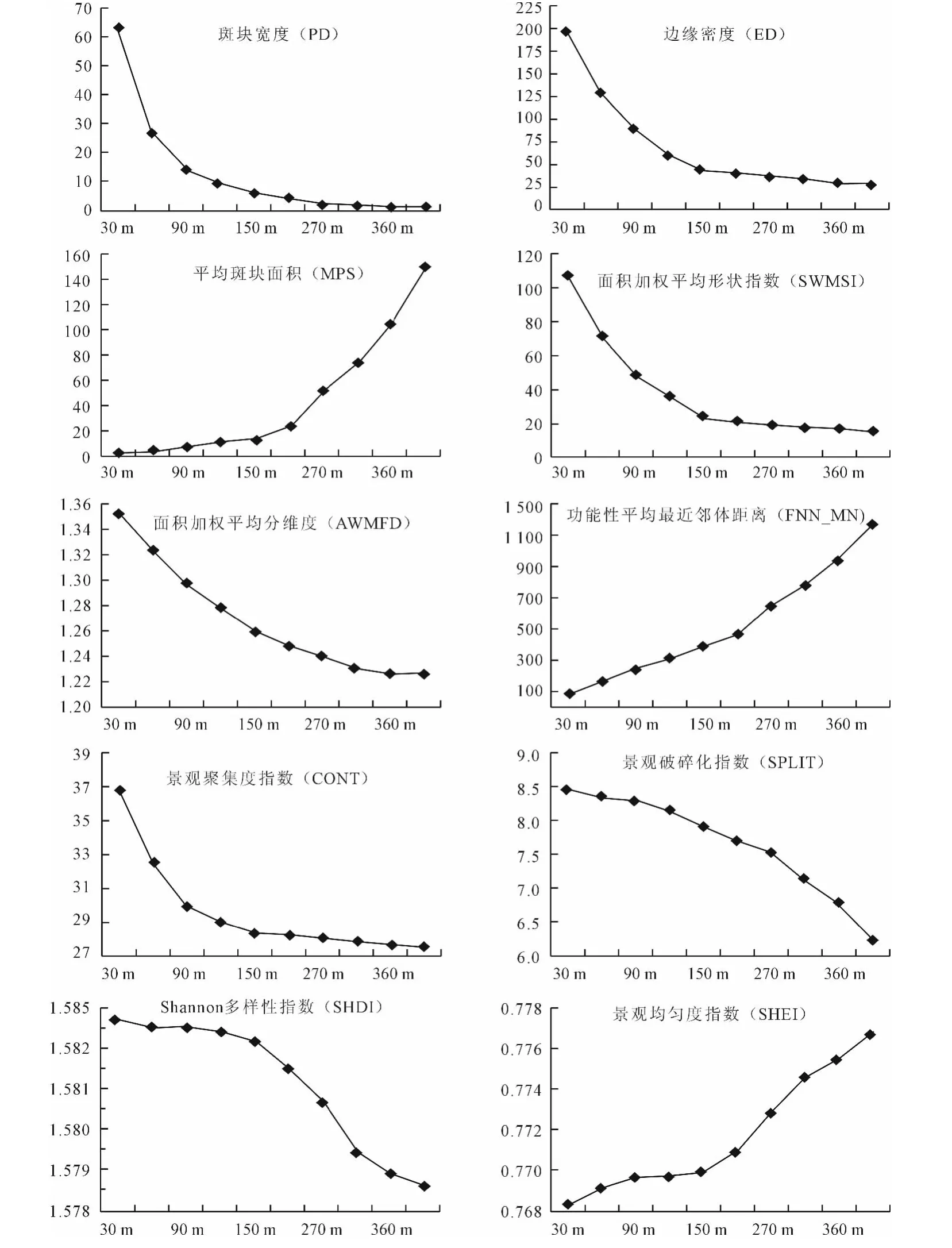
图3 景观层次上景观格局指数的空间粒度

3.1.2 景观格局的空间自相关性及其对粒度变化的响应

在各粒度水平下，Moran＇s I衍生统计量均大于＋1.65（图4），表明研究区域内的景观格局存在着显著空间正自相关性。总体而言，随着粒度增大，Moran＇s I衍生统计量z曲线值呈下降趋势。尤其在粒度30～150 m范围内，z曲线表现出一个快速下降的过程；当粒度超出150m后，曲线下降趋势逐渐减缓。各斑块在空间分布上的依赖性具有明显的尺度特征。当粒度较小时（30～150m），各斑块在邻近范围内的变化往往表现出一定的自相似性，而当粒度逐渐增加时，相邻景观的差异急剧增加，相似性减小。显然，150m的粒度水平为景观空间自相关性对尺度响应的一个敏感点，这说明150m分辨率有可能是该景观格局的本征尺度。当研究粒度超出150m范围后，各斑块空间自相关性缓慢减小，其粒度效应也逐渐减缓。

3.2 景观生态指数的幅度效应

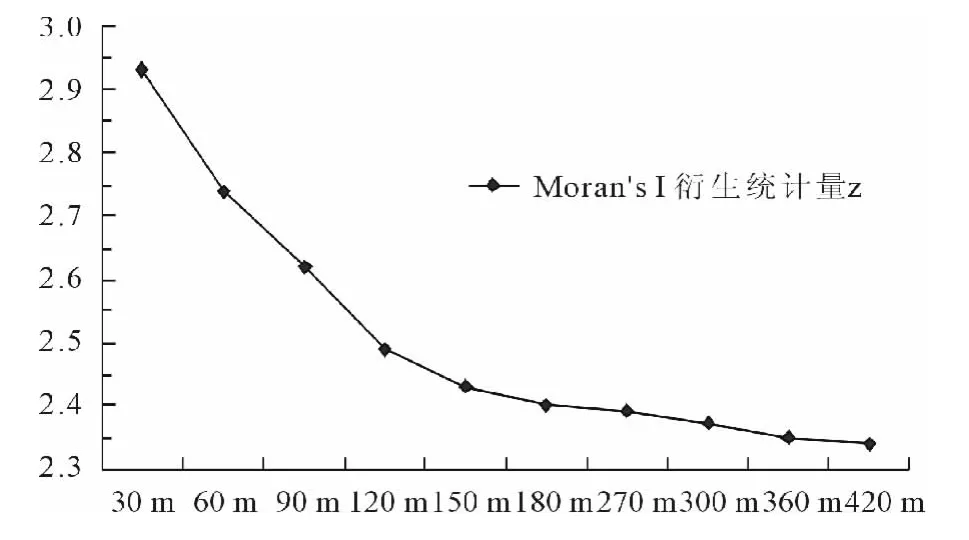
图4 Moran＇s I衍生统计量z指数对粒度变化的响应

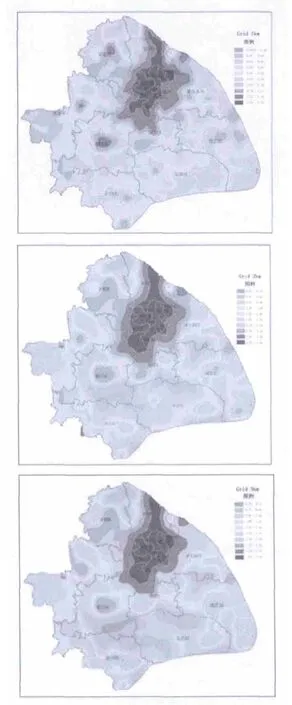
图5 不同幅度下景观多样性的空间格局

分别选择1km、2km和3km这3种空间幅度，以150m为粒度，对于每一空间幅度计算SHDI，分析在不同幅度下景观多样性的空间特征，并利用半变异函数分析不同幅度下SHDI、AI、AWMFD和SPILT的空间异质性及其尺度依赖性。

3.2.1 幅度变化对景观多样性的影响

图5显示了不同幅度下上海陆域范围景观多样性的空间格局。从图中可见，幅度对景观多样性的空间分布存在较大影响。在1km幅度下，景观多样性格局具有两个明显的特点：一是空间格局复杂，空间差异显著；二是在城市化明显的区域从内到外依次出现“高低值相间”的环状扩展模式。景观多样性的高值区域均分布在城市化程度高的区域，如上海外环线以内区域、市镇中心区域等，并且从高值区域向周边扩散，形成由高到低的圈层结构。在2km幅度下，景观多样性格局的总体趋势没有改变，但空间分布趋于简单，空间变化减少；仍存在着以高度城市化区域为核心的“高值 低值”的圈层结构，但高值区域的面积与1km幅度相比，有向中心紧缩的趋势，圈层结构更加明显。而在3km幅度下，多样性的空间差异趋于缩小，有些在1km、2km幅度下表现出的高值区此时由于幅度的增大而掩盖了其与周边区域的差异，从而导致这些高值区域的消失，此现象在奉贤区尤为明显；同时由于幅度的增大，有些圈层表现出逐渐合并的趋势。

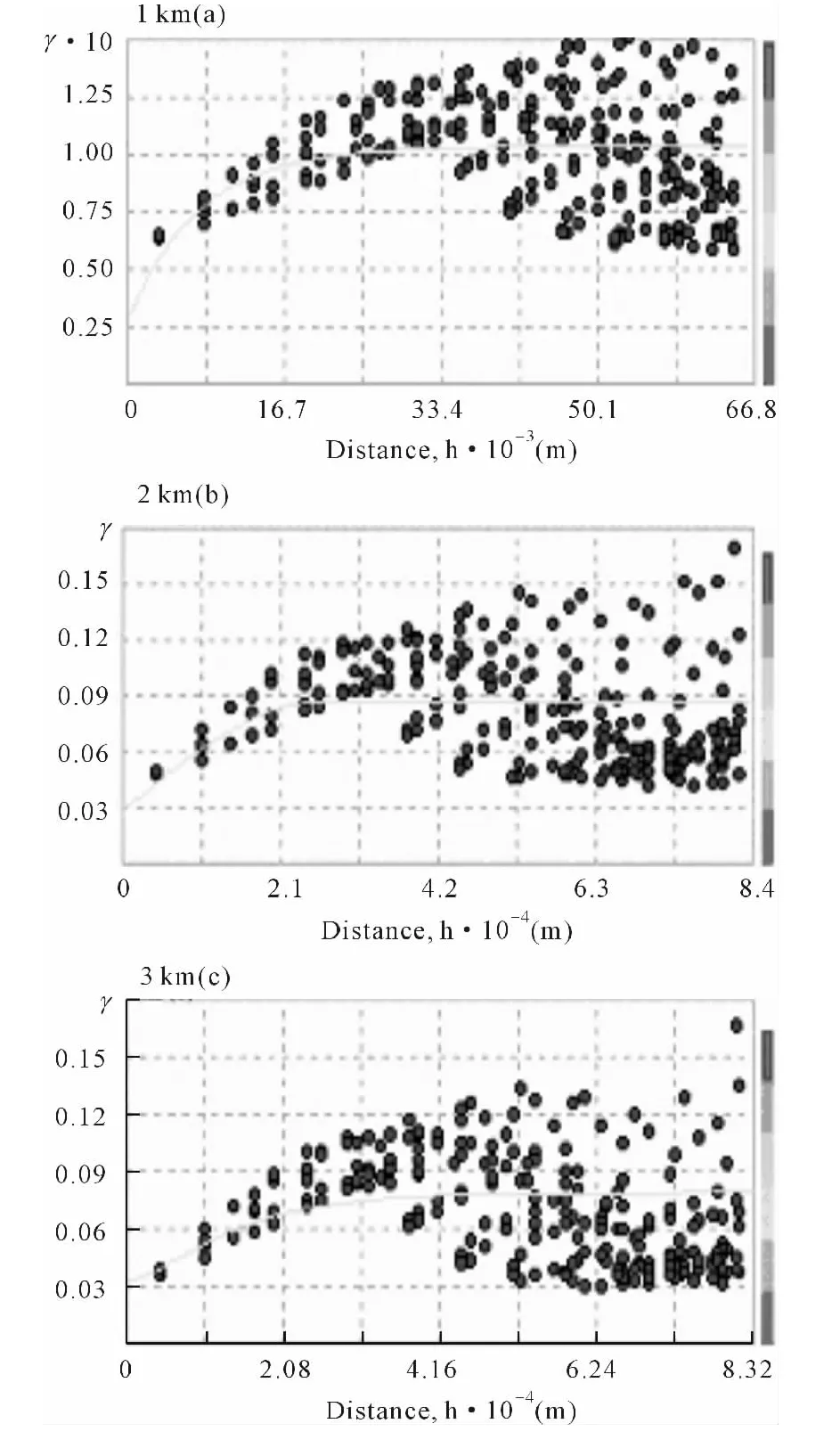
图6 三种幅度下Shannon多样性指数的半变异函数

在3种不同的幅度下，不仅景观多样性的空间格局发生了变化，而且SHDI值域范围也发生了改变。1km幅度下，SHDI的变化区间为0.0001～1.71，2km幅度下则减小为0.01～1.63，而到3km幅度时，则继续减小至0.1～1.59。可见，幅度的改变不但影响到景观多样性的空间分布格局，而且也改变多样性指数的大小。幅度越大，多样性指数越趋于一致，变化区间减小。

3.2.2 景观生态指数对幅度变化的响应

利用ArcGIS9.1的地统计学模块，按照半变异函数原理分别对SHDI所有样本计算半变异函数。图6和表2分别显示了不同幅度下SHDI半变异函数的特征、模型及其参数。

表2 不同幅度下景观多样性半变异函数的理论模型及参数

从图6和表2中可以看出上海市陆域范围内景观SHDI具有明显的空间自相关性：距离较小时，空间变异也较小，在一定距离范围内，SHDI的空间变异与距离呈正相关，当距离增加时，相似性减小，SHDI在空间上的差异也增加，半变异函数增大。

图6显示SHDI的半变异函数在不同的幅度下差异十分显著。根据对半变异曲线的拟合，各幅度下的理论模型和参数是有差别的。1km幅度下，理论模型符合指数变化特征，其中表示随机部分空间异质性的块金值Co为0.028，表示系统总的空间变异程度的基台值Co＋C为0.1036，而Co/Co＋C为0.2699，反映了随机部分引起的空间异质性占总空间异质性的比重。Co＝0.028说明1km幅度尽管对研究区域而言已经是一个较小的尺度了，但多样性的空间变异可能仍然具有尺度或测量误差等随机因素的作用，这一贡献比约为26.99%。基台值中除去Co，其余的空间变异则是由空间自相关贡献的，约占73%。

同理，我们得到在2km和3km幅度下半变异函数的理论模型分别为球状模型和K－Bessel模型。从图6可见，随着幅度不断增加，块金值不断增加，块金效应逐渐增强，表明随机部分引起的空间异质性的比例逐渐增大，而空间自相关部分引起的空间异质性的贡献则减小。随机因素主要包括尺度影响和测量误差，本研究各个幅度测量误差是一定的，这样就说明随着尺度的增加，掩盖了该尺度内部较小尺度上的空间变异特征，尺度所产生的误差则以块金效应表现出来。

变程揭示了多样性空间依赖性的距离，在1km幅度，多样性的空间自相关出现在局部范围（22.94km），当超过22.94km后，空间自相关就不存在了。随着幅度增加，变程也增加，在3km幅度下，变程已增加至37km，说明SHDI在更大的范围内存在空间依赖性。

采用同样方法，对不同幅度下CONT、AWMFD和SPILT所有样本计算半变异函数，表3～5给出了不同幅度的上述各指数半变异函数模型及其参数。

表3 不同幅度下景观聚集度指数半变异函数的理论模型及参数

表4 不同幅度下面积加权平均分维数指数半变异函数的理论模型及参数

表5 不同幅度下景观破碎化指数半变异函数的理论模型及参数

CONT反映景观中各类斑块的非随机性或聚集程度。从表3可见，在1km和2km幅度下，理论模型均符合指数变化，随着幅度增大，块金值Co急剧下降，基台值Co＋C也有所下降，相应的Co/Co＋C明显减小。当幅度增大到3km时，其理论模型为二次方程式，但块金值Co和基台值Co＋C相对于2km幅度下又有所上升，分别为11.736和91.7146，Co/Co＋C也增大为0.1278。由此可见，在1km幅度下，可能由于幅度太小，使过多的局部细小规律和圈层特征显现出来，反而使CONT的空间异质性增加，并且随机部分的贡献较大，块金效应也最强；当幅度增大到2km时，局部规律逐渐被总体规律性所掩盖，CONT空间异质性的特征趋于简单，随机部分的空间异质性和系统的最大变异性均减小，块金效应较弱；当幅度增大到3km时，聚集度在较小范围内的变化被忽视，部分空间规律信息由于尺度效应而损失，聚集度空间自相关性引起的空间差异对总体变异的贡献又有所减小，块金效应增强。

从变程变化的特征可知，在1km幅度下，CONT空间自相关出现在局部范围（21.91km），随着幅度增加，变程也增加，在3km幅度下，变程已增加至26.83km，说明CONT在更大的范围内存在空间依赖性。

AWMFD可用于测定斑块形状，反映景观或斑块边缘形状的复杂性和变异性，这将影响斑块内部和斑块之间的生态过程，如动物迁移、物质交流等。由表4可以看出，从1km到3km，块金值逐渐增加，说明分维数空间异质性的尺度效应逐渐增强；Co/Co＋C比值逐渐增大，表明空间自相关性对总体变异的贡献逐渐减小。值得注意的是，AWMFD的变程随着研究幅度的增加而略有减小，说明幅度增加，AWMFD的空间依赖性范围略有缩小。

SPILT表征景观的破碎程度，反映景观空间结构的复杂性，在一定程度上反映了人类对景观的干扰程度，进而反映出人类对自然生态系统的影响。由表5可见，在三个幅度下，理论模型均符合球状模型，但其块金值Co从1km到3km表现为增大的趋势，且从2km到3km增加较快，由0.1683增大至0.1851，可见，SPILT的块金效应随着幅度的增加而增大。基台值Co＋C在1～3km间表现为先减小后增大，其总的空间变异性在2km时最小。Co/Co＋C比值在1～3km间有一个先增大后减小的趋势，随机部分引起的空间异质性的比重在2km时最大。SPILT在2km幅度下的变程最大，表明在2km幅度时，空间自相关的存在范围最大。

根据标准均方根预测误差越接近于1，半变异函数模型的拟合结果越好的原则［27］，由表2～5可知，除AWMFD外，选择2km对于研究上海市陆域范围景观格局的空间变化是一个比较合适的尺度。

4 结论

本文以上海陆域范围为研究区域，采用2004年Landsat TM图像解译的土地利用为基础数据，在空间粒度方面，从斑块类型和景观两个层次，探讨了20种景观生态指标的粒度效应；利用Moran＇s I指数对不同粒度下景观生态格局的空间自相关性进行分析。在此基础上，利用半变异函数探讨这些景观生态指标的空间异质性与幅度的效应关系，揭示景观空间异质性的尺度依赖性。主要结论如下。

（1）在斑块类型层次，PLAND、LPI、DIVISION 的值基本不随空间粒度变化，粒度效应不明显。其他指数均表现出明显的粒度效应：PD、ED、AWMSI、AWMFD和AI值随粒度的增大而减小；MPS和FNN＿MN的值随粒度的变粗而增加。上述部分指数或某些斑块类型的指数出现明显的尺度转折点。农田和建筑用地是研究区域内的优势斑块，其MPS和AWMSI值大致分别在180m和120m附近出现尺度转折点。PD值和AI值则分别在120～150m左右和90～120m附近出现尺度转折点。

（2）在景观层次，各景观生态指数的粒度效应明显。PD、ED、AWMSI和CONT值随粒度的增大而减小，且在150m附近存在较明显的尺度拐点；AWMFD、SPILT和SHDI值随粒度的增大将最终下降，但尺度转折点不明显或粒度效应曲线较复杂；MPS值随粒度的变粗而增加，并在120～180m之间出现尺度转折。FNN＿MN和SHEI值随粒度的增大将最终上升，但尺度转折点不明显或粒度效应曲线较复杂。

（3）上海市陆域范围的景观格局存在着显著正空间自相关关系，150m的粒度水平为景观空间自相关性对尺度响应的一个敏感点。

（4）SHDI和CONT的半变异函数在不同的幅度下差异十分显著，而AWMFD和SPILT半变异函数对于不同幅度的差异相对较小。不同景观指数在不同幅度下的空间异质性表现及其变化规律差异较大。随着幅度的增加，SHDI和AWMFD半变异函数的块金值逐渐增加，Co/Co＋C值也逐渐增大，块金效应增强，表明空间自相关性对总体变异的贡献逐渐减小。对于CONT和SPILT，分别在1km和2km幅度下，Co/Co＋C比值最大，块金效应最强。

（5）对于SHDI和CONT，随着幅度的增加，变程逐渐增大，空间自相关的存在范围增大；对于AWMFD，随着幅度的增加，变程略有减小，空间依赖性的存在范围略有减小；对于SPILT，随着幅度的增加，变程先增加，后又略减小，空间依赖性的存在范围在2km时最大。

（6）半变异函数模型的拟合结果表明，对于SHDI、CONT和SPILT，2km对于研究上海市陆域范围景观格局的空间变化是一个比较合适的尺度。

［1］傅伯杰，陈利项，马克明.景观生态学原理及应用［M］.北京：科学出版社，2001.

［2］王仰麟.渭南地区景观生态规划与设计［J］.自然资源学报，1995，10（4）：372－379.

［3］邬建国.景观生态学——格局、过程、尺度与等级［M］.北京：高等教育出版社，2000.

［4］Marceau D J.The scale issue in social and natural sciences［J］.Canadian Journal of Remote Sensing，1999，25：347～356.

［5］岳文泽，徐建华，谈文琦，等.城市景观多样性的空间尺度分析——以上海市外环线以内区域为例［J］.生态学报，2005，25（1）：122～128.

［6］邬建国.景观生态学——概念与理论［J］.生态学杂志，2000，19（1）：42～52.

［7］Lam N S N，Quattrochi D A.On the issues of scale，resolution，and fractal analysis in the mapping sciences［J］.Prof Geogr，1992，44（1）：42～46.

［8］Wu J G，Jelinski D E，Luck M，et al.Multiscale analysis of landscape heterogeneity：Scale Variance and Pattern Metrics［J］.Geographic Information Sciences，2000，6（1）：6～19.

［9］Veerle V E，Marc A.A stepwise multi－scaled landscape typology and characterisation for trans－regional integration，applied on the federal state of Belgium［J］.Landscape and Urban Planning，2009，3（91）：160～170.

［10］申卫军，邬建国，林永标.空间粒度变化对景观格局分析的影响［J］.生态学报，2003，23（12）：2506～2519.

［11］Montserrat B，Lourdes C，F.Xavier Sans.Vegetation patchiness of field boundaries in the Mediterranean region：The effect of farming management and the surrounding landscape analysed at multiple spatial scales［J］.Landscape and Urban Planning，2012，1（106）：35～43.

［12］Theano S T.New landscape spatialities：the changing scales of function and symbolism［J］.Landscape and Urban Planning，2005，1（70）：165～176.

［13］李秀珍，布仁仓，常 禹.景观格局指标对不同景观格局的反应［J］.生态学报，2004，24（1）：123～134.

［14］赵文武，傅伯杰，陈利顶.景观指数的粒度变化效应［J］.第四纪研究，2003，23（3）：326～333.

［15］Wu J.Effects of change scale on landscape pattern analysis：scaling relations［J］.Landscape Ecology，2003，42（9）：489～503.

［16］Wu J，Shen W，Sun W，et al.Empirical patterns of the effects of changing scale on landscape metrics［J］.Landscape Ecology，2002，17（5）：761～782.

［17］Li H，Wu J.Use and misuse of landscape indices［J］.Landscape Ecology，2004，19（7）：854～867.

［18］徐建华，岳文泽，谈文琦.城市景观格局尺度效应的空间统计规律——以上海中心城区为例［J］.地理学报，2004，59（6）：1058～1067.

［19］刘纪远.中国资源环境遥感宏观调查与动态研究［M］.北京：中国科学技术出版社，1996.

［20］宋治清，王仰麟.城市景观格局动态及其规划的生态学探讨［J］.地球科学进展，2005，20（8）：840～849.

［21］Albert L，Joan N.Indicators of landscape fragmentation：The case for combining ecological indices and the perceptive approach［J］.Ecological Indicators，2012，1（15）：85～91.

［22］Robert C C，Joan I N.Limitations of using landscape pattern indices to evaluate the ecological consequences of alternative plans and designs［J］.Landscape and Urban Planning，2005，4（72）：265～280.

［23］Sen A K.Large sample－size distributions of statistics used in testing for spatial correlation［J］.Geographical Analysis，1976，9：175～184.

［24］曾 辉，江子瀛，孔宁宁.快速城市化景观格局的空间自相关特征分析——以深圳市龙华地区为例［J］.北京大学学报：自然科学版，2000，36（6）：824～831.

［25］王政权.地统计学及在生态学中的应用［M］.北京：科学出版社，1999.

［26］肖笃宁，赵 羿，孙中伟.沈阳西郊景观格局变化的研究［J］.应用生态学报，1990，1（1）：75～84.

［27］汤国安，杨 昕.ArcGIS地理信息系统空间分析实验教程［M］.北京：科学出版社，2006.