约束泛最小二乘估计及其Cook距离

卢冬晖，江秉华，伍 丽

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

0 引言

对普通线性模型

y=Xβ+e,E(e)=0,Cov(e)=σ2I

胡宏昌教授从两方面推广得到泛最小二乘估计。一是统计上的自然推广，在X不是满秩时，人们为了得到唯一解，必然增加新的求解条件，比如在β′β=min的条件下，得到最小二乘范数估计。还有作者用过β′Pβ=min 的条件。第二个方面是20世纪初，Hadamard观察到求解算子方程Wf=F的问题是不适定的。20世纪60年代中期，人们发现，如果极小化正则化泛函：R(β)=λρ(e)+kf(β)=min,则可以得到一个解序列，它在δ→0 时收敛于所希望的解。将此正则化思想用于上面的线性模型，即寻求使R*(β)=‖y-Xβ‖2+k‖β‖2最小化的参数。这样得到条件e′Pe+kβ′Qβ=min .把上面两个同样的条件进一步一般化，可以得到R(β)=λρ(e)+kf(β)=min[1].但是实际应用中通常还是考虑e′Pe+kβ′Qβ=min.

影响分析是统计诊断的一种重要方法，目的是探测数据中对既定模型的统计推断影响特别大的点。[2]1977年Cook定义了Cook距离，提出了点删除法这种经典影响分析方法[3]。这种方法已经被用于许多模型的影响分析，如普通线性模型的影响分析，增长曲线的影响分析等[4]。影响分析也可能会出现“淹没”或“掩盖”现象[5～6]。还有一些研究致力于对Cook距离的推广和化简。

下面用条件极值法得到约束泛最小二乘估计，再定义其Cook距离并进行化简。

1 约束泛最小二乘估计

对普通线性模型:

y=Xβ+e,E(e)=0,Cov(e)=σ2I

(1)

其中y为n维观测列向量，X为n×p已知设计矩阵,β为p维未知参数列向量，e为随机误差列向量。

作函数φ(β)=e′Pe+kβ′Qβ，k是非负实数，P,Q是给定正定矩阵。

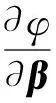
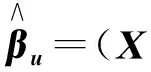
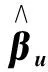
在一些场合，我们需要求带一定线性约束的泛最小二乘估计。

定理1 对线性模型(1)假设:

Rank(A)=k

(2)

是一个线性相容方程组，A为k×p已知矩阵，且Rank(A)=k，b为k×1 已知向量， 则模型(1)在约束条件(2) 下的泛最小二乘估计为：

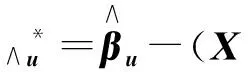
证明：为了用Lagrange乘子法求模型(1)满足Aβ=b的泛最小二乘估计，作辅助函数：

L(β,λ)=e′Pe+kβ′Qβ+2λ′(Aβ-b)

其中λ=(λ1,λ2…λk)′为Lagrange乘子。

对函数L(β,λ) 求对β的偏导，并令其为零，得：

-2X′P(y-Xβ)+2kQβ+2A′λ=0

即X′Py-X′PXβ-kQβ-A′λ=0

(3)

(X′PX+kQ)β=X′Py-A′λ

两边左乘 (X′PX+kQ)-1得：

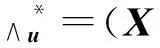
(4)

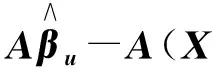
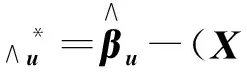
2 约束泛最小二乘估计的Cook距离

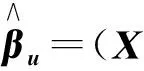
因为P是正定矩阵，故存在可逆矩阵T，使得P=T′T，把y=Xβ+e两边同时左乘T，得Ty=TXβ+Te，令Y=Ty,Z=TX,e*=Te,则得到

Y=Zβ+e*

(5)

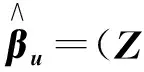
(6)

(7)

先引入以下记号，Y(i)，y(i)分别表示从矩阵Y删除第i行后的矩阵和被删除的第i行向量。后面以此类推，不再逐一说明。

从模型(5)删除第i组数据后的n-1组数据的线性回归模型为：

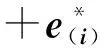
其约束泛最小二乘估计为：

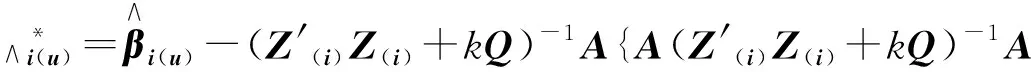
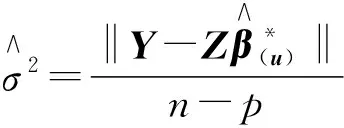
定义：基于约束泛最小二乘估计的回归模型(5)的Cook距离为：

(8)

注：当k=0时上述定义即Cook在文献[2]中所定义的距离，说明此处定义是合理的。

引理 令S=Z′Z+kQ，H=ZS-1Z′=Z(Z′Z+kQ)-1Z′,M=A′(AS-1A′)A,N=ZS-1MS-1Z′,设hii,nii分别为H、M的对角元，则：

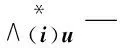
证明：设K为n×n可逆矩阵，u,v均为n×1向量。则有恒等式：

(9)

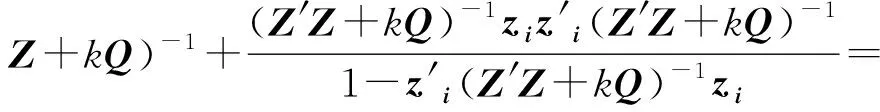
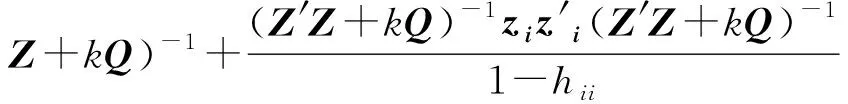
同样利用(9)式得：

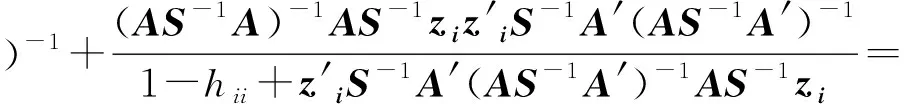
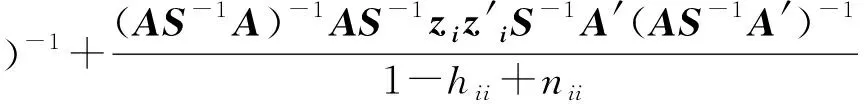
(10)

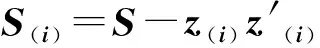
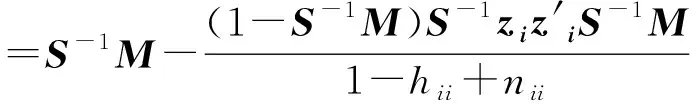
把上式代入下面可得：

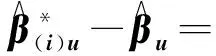
{S(i)-1A′(AS(i)-1A′)-1-S-1A′(A-1A′)-1}b=

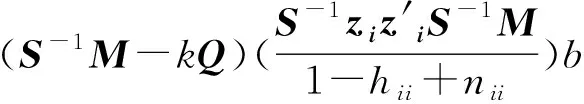
(11)

为继续化简，用文献[7]p.p50定理3.4.2中同样的方法可以得出以下公式：

(12)

将(12)代入(11)，得：

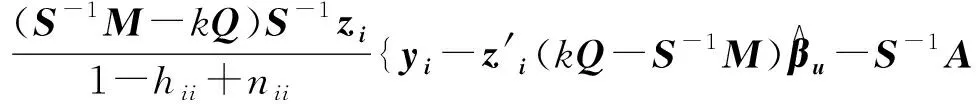
(13)

定理2 约束泛二乘最小估计的Cook距离可以化简为：

(14)

其中fii为F=ZS-1MS-1MS-1Z′ 的第i个对角元，lii为L=ZS-1(QM+MQ)S-1Z′ 的第i个对角元，gii为G=ZS-1QSQS-1Z′ 的第i个对角元。

证明 将(13)式代入(8)式得：

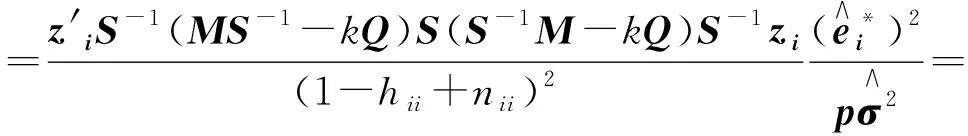
利用公式(14)，在计算Cook统计量时，就不需要对每一个不完全数据的线性模型进行计算，而只需要计算出H,N,W的对角元即可。

注：对k,P,Q取特定值和矩阵时，可以得到相应估计的Cook距离化简公式。

3 结论与进一步的问题

我们得到约束泛最小二乘估计，但是对更一般的情况，比如目标函数取R(β)=λP(e)+kf(β)的情况的讨论，目前结果不多[1]。用迭代算法或泰勒公式，也可以得到Cook统计量的近似简化公式，而且可以有明确的统计意义。[9]当然通常情况下若是能得到非近似公式还是更有利于理论推导和实际计算。

参考文献：

[1]胡宏昌,崔恒建,秦永松,等.近代线性回归分析方法[M].北京:科学出版社,2013.

[2]Cook R D. Dectection of Influential Observation in Linear Regression[J]. Tochnometrics, 1977,19(1):15～18.

[3]Pan J X,Fang K T.Growth Curve Models and Statistical Diagnostics[M].New York:Spring,2002.

[4]Rousseeuw P J,Zomeren B C. Ummasking multivariate outliers and leverage points[C] . Journal of the Amercian Statistical Association, 1990,85:633～639.

[5]Jose A Diaz-Gracia , Grciela Gonzalez-Farias . A note on the Cook's distance[C] . Journal of Statistical Planning and Inference, 2004,120:119～136.

[6]Choongrak Kim.Cook's distance in local polynomial regression[C].Statistical &Probability Letters,2001,54:33～40.

[7]王松桂.线性统计模型[M].北京:高等教育出版社,1999.

[8]费 宇,潘建新.线性混合效应模型影响分析[M].北京:科学出版社,2005.