波浪谱形对不规则波数值模拟的影响

吴喜德

(交通运输部 水运科学研究院，北京 100088)

波浪是近岸区域关键的水动力要素，不仅影响影响港工建筑物安全和船舶泊稳，也是近岸物质输运的主要动力要素。外海向近岸传播来的波浪随机性较强，受近岸水深、岸线、海岸建筑物等影响，波浪的折射、绕射、汇聚等各种效应异常显著，在海岸工程中需要分析研究不规则波浪在近岸的传播分布。为便于对不规则波处理，通常采用波浪谱将不规则波浪分解为由无限多个振幅不同、频率不同、方向不同、位相杂乱的规则波组成。不规则波浪数值模拟中，通常需要将这些组成波分别进行模拟后再经过综合叠加来模拟波浪传播，这势必会造成计算量的大大增加。缓坡方程综合考虑了波浪传播的折射、绕射等效应，是一类常用的近岸线性波浪模型[1-9]，由于该类方程基于线形波浪理论而来，如果可以忽略入射波浪谱形的影响，采用规则入射波来代替不规则入射波势必会大大减少计算工作量，提高计算效率。

本研究利用将数值模拟分析了波浪谱形对不规则波浪数值模拟结果的影响。研究中，采用不同参数的JONSWAP谱来模拟不规则入射波浪要素分布，采用波浪抛物型缓坡方程来模拟近岸波浪传播，通过模拟结果的比较来分析波浪谱形状对模拟结果的影响。

1 数学模型

1.1 JONSWA波浪谱

波浪谱描述了不规则波浪能量在频率上的分布，在波浪的理论研究和实际应用中都有十分重要的意义。波浪谱形状依据波浪能量在波高、周期和波向等的分布而定，是波浪周期、波高和波向等的函数。JONSWAP谱是近岸海域应用较为广泛的一种波浪谱，由英、美、法等多国研究人员在开发北海的北海海浪联合课题中提出，随后多位学者对其进行了改进并得到了广泛应用。本研究采用改进的JONSWA谱[10]对不规则波进行离散：

(1)

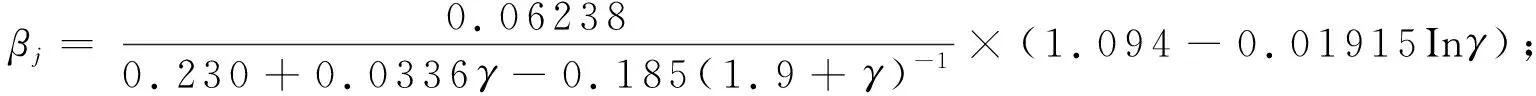
式中，f为波浪频率；fp为谱峰频率；γ为谱峰因子，取值介于1.5～6，平均值为3.3，对波浪能量分布有重要影响，γ越大谱波浪能量越集中，改变γ的取值可得到不同形状的谱。

1.2 抛物型缓坡方程模型

抛物型缓坡方程在椭圆型缓坡方程[1]中忽略了波浪在主传播方向上的反射、折射等作用的影响，即忽略了波向线方向的绕射作用而仅考虑沿波峰方向的绕射，而综合了波浪的折射和绕射，求解大为简化，克服了椭圆型缓坡方程数值求解不够高效、计算较困难的缺陷。Kirby基于低阶极值原理提出了低阶极值抛物型缓坡方程[3]，考虑到波浪不规则性，表示为[4]

(2)

其中,

(3)

(4)

非线性项Dn的表达式为

(5)

(6)

采用有限差分法对方程(2)进行数值离散求解[4]。

2 数值模拟与结果分析

为了分析波浪谱形状分布对不规则波浪数值模拟结果的影响，通过在JONSWAP波浪谱采用不同的谱峰因子来得到不同分布形状的波浪谱。基于这些谱来模拟入射波浪要素分布。数值模拟时，依据采用的JONSWAP谱按等分频率法将入射波浪要素划分为50份，为了避免所模拟的组成波浪频率成周期性重复，在各频率划分区域范围内随机选取频率作为该区间的代表频率。

2.1 近岸平直斜坡地形上不规则波浪传播的模拟分析

海岸和近海工程国家重点实验室对近岸入射波浪在1：40和1：100平直地形上的传播进行了模拟[4-6]。表1为其中3个实验工况，其中h0为波浪入射处静水深；θ0为入射波浪传播方向；H0为入射波高；T0为入射波浪周期。模拟中分别采用谱峰因子γ=2.0，4.0，3.3，6.0的JONSWAP谱模拟入射波浪要素分布，图1给出了3个工况中不同谱峰因子对应的JONSWAP谱。图2给出了工况1，2，3中不同谱峰因子γ=2.0，4.0，3.3，6.0的JONSWAP入射波浪谱时，所模拟的波高和实测值的比较。可以看出采用不同谱形波浪谱模拟的波高和实测值均比较一致，且依据各谱形模拟所得波高基本一致。但采用规则波模拟所得结果和不规则波模拟结果有些差别，在波浪破碎区尤为明显，这主要归于模型中非线性项D和波浪破碎能量耗损因子的影响。总体来看，模拟中入射波浪谱形分布对模拟结果没有明显影响。

表1 近岸平直斜坡地形上波浪传播的模拟参数Table 1 Parameters for the wave propagation on a straight slope in the nearshore area

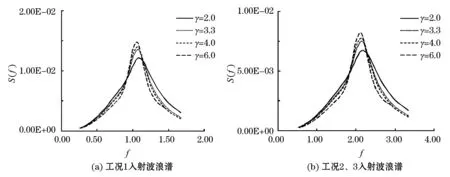
图1 近岸平直斜坡地形入射波浪JONSWAP谱Fig.1 The JONSWAP spectrum of the incident waves propagating on a straight slope in the nearshore area

图2 近岸平直斜坡地形上波浪传播模拟Fig.2 The Simulation of wave propagation on a straight slope in the nearshore area

2.2 圆形浅滩地形上不规则波浪传播的模拟分析

Ito和Tanimoto进行了圆形浅滩地形上规则波浪传播的模型实验[11]，并给出了3个断面的实测结果。其中平底区域的水深为0.15 m，圆形浅滩的水深为

h=0.05+0.15625(x-1.2)2+(y-1.2)2

(8)

波高为0.010 4 m；周期为0.511 s的规则入射波浪沿x轴正向传入计算区域。

模拟中，采用均匀网格划分计算区域，计算的x,y向空间步长均取0.1 m。为了考察不规则波浪的传播，分别采用谱峰因子γ=2.0，4.0，3.3，6.0的JONSWAP谱模拟入射波浪要素分布，图3给出了不同谱峰因子对应的JONSWAP谱。图4给出了不同谱峰因子γ=2.0，4.0，3.3，6.0的JONSWAP入射波浪谱时，3个实测断面所模拟的波高和实测值的比较，可以看出在3个实测断面采用不同谱形模拟的波高和实测值均比较一致，且依据各谱形模拟所得波高均很接近。但采用规则波模拟所得结果和不规则波模拟结果有些差别，这主要归于模型中非线性项的影响。总体来看，模拟中入射波浪谱形分布对模拟结果没有明显影响。

图3 圆形浅滩地形入射波浪JONSWAP谱Fig.3 The JONSWAP spectrum of the incident waves propagating on a circular shoal

图4 圆形浅滩地形上波浪传播模拟Fig.4 The Simulation of wave propagation on a circular shoal

3 结 语

海岸工程中，常常需要分析不规则波浪在近岸的传播分布特性。本研究通过数值模拟分析了入射波浪谱形状对不规则波浪数值模拟结果的影响。研究中采用不同参数的JONSWAP谱模拟入射波浪要素分布，基于缓坡方程波浪模型模拟不规则波浪的传播，分析了波浪谱形状对波浪数值模拟结果的影响。模拟结果表明，在采用近岸缓坡方程模拟不规则波浪时，入射波浪谱形分布对模拟结果影响不明显，但和采用规则波模拟所得结果有些差别，主要归于波浪模型中非线性项的影响。

参考文献：

[1] BERKHOFF J C W, BOOIJ N, RADDER A C. Verification of numerical wave propagation models for simple harmonic linear water waves [J]. Coastal Engineering, 1982, 6(3): 255-279.

[2] TANG J, SHEN Y M, ZHENG Y H, et al. An efficient and flexible computational model for solving the mild slope equation [J]. Coastal Engineering, 2004, 51(2): 143-154.

[3] KIRBY, J T. Rational approximations in the parabolic equation method for water waves [J]. Coastal Engineering, 1986, 10(4), 355-378.

[4] 唐军, 沈永明, 崔雷,等. 近岸波浪破碎区不规则波浪的数值模拟[J]. 海洋学报, 2008, 30(2): 147-152.

[5] TANG J, SHEN Y M, CUI L. Modeling near-shore currents induced by irregular breaking wave [J]. Journal of Coastal Research, 2008, SI52: 245-252.

[6] 唐军, 沈永明, 崔雷，等. 随机波浪作用下近岸波流场的数值模拟[J]. 力学学报, 2008, 40(4): 455-463.

[7] TANG J, SHEN Y M, QIU D H. Numerical study of pollutant movement in waves and wave-induced long-shore currents in surf zone [J]. Acta Oceanologica Sinica, 2008, 27(1): 122-131.

[8] 唐军, 沈永明, 崔雷. 基于抛物型缓坡方程模拟近岸植被区波浪传播[J]. 海洋学报, 2011, 33(1):7-11.

[9] TANG J, SHEN Y M, SHI F, et al. Numerical study of wave and longshore current interaction [J]. Acta Oceanologica Sinica, 2012, 31(3): 10-17.

[10] GODA Y. A comparative review on the functional forms of directional wave spectrum [J]. Coastal Engineering Journal, 1999, 41(1), 1-20.

[11] ITO Y, TANIMOTO K. A method of numerical analysis of wave propagation-application to wave diffraction and refraction [C]∥Proceeding of the 13th Coastal Engineering Conference. Vancouver, ASCE, 1972:503-522.