COSMOS Motion在CT床优化设计中的应用
尚洪,黄坚,任超
1 上海西门子医疗器械有限公司,上海市,201318
2 上海西门子研究院,上海市,200082
0 引言
CT床是计算机断层扫描系统中重要组成部分,是将病人送入Gantry进行扫描检测的载体,其性能直接影响扫描测试结果的精度,合理的CT床结构设计不仅自身直接降低成本,还为测试及数据处理提供了便利[1]。CT床的床身通常采用平行四边形机构,其受力的复杂性及运动位置的多变性为零部件的选型带来困难。以往CT床设计时所采用的“设计-试验-再设计”方法不仅难以精确分析零部件受力,还提高了CT床的研发成本并延长了新产品的上市时间。
多刚体动力学仿真分析主要应用于机构的运动和受力分析计算,具有高效、精确、系统等特点,尤其适用于系统概念设计阶段[2]。本文借助COSMOS Motion软件,对CT床的各种工况进行了仿真分析,并优化了铰链的位置,为铰链轴承和驱动电机的选型提供依据,定量的验证了病床结构设计的合理性,有效提高了CT床设计质量并降低了研发成本。
1 CT床工作原理
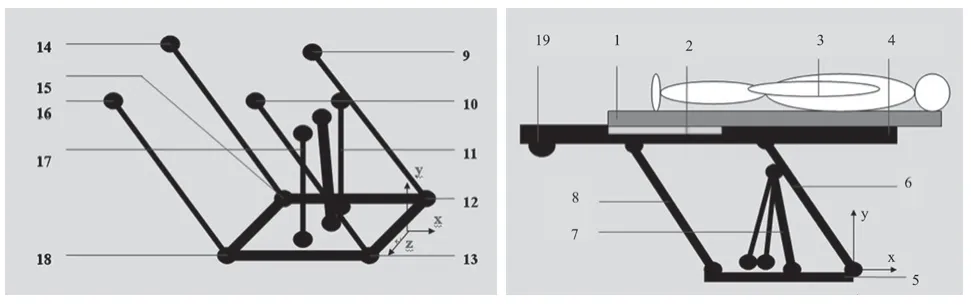
图1 CT床结构模型Fig.1 CT table structure model
CT床结构可分为床身、驱动件、升降支撑组件和床板四大部分组成,如图1所示。床体平行四边形机构由前摆杆、后摆杆、底座和床架构成,床身的升降运动由电动直线制动器和气弹簧实现,由于直线制动器体积较大,直线制动器的作用点关于床板Z方向不对称,因此模型不能做对称性简化。载荷由床板和支撑板构成,其水平运动由直流电机-同步带实现。床体工作时,直线制动器以一定的速度将床体从38o起升角的位置提升到80o位置后,水平直流电机再以一定的速度将拖车同病人一同传送到Gantry内,最大行程为1600 mm。扫描测试结束后,以相反运动方式回到起始位置。
2 CT床仿真模型的建立
2.1 定义配合副
COSMOS Motion 与Solidworks 实现了无缝集合,Solidworks模型中的约束可自动转化为COSMOS Motion中相应的配合副,并对冗余约束进行套筒技术处理[3]。参照图1所示零件号,表1给出了CT床所有组件的装配约束关系。
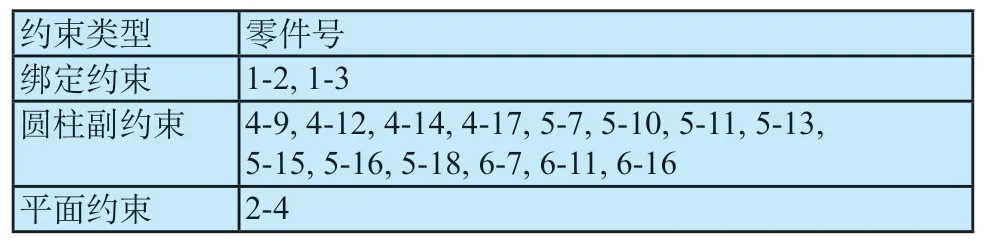
表1 CAD装配体中的约束Tab.1 CAD assembly constraints
2.2 定义材料属性
CT床中床板由泡沫填充物和增强碳纤维构成,因增强相质量较低且不考虑其刚度,因此定义床板密度为580 kg/m3,其余部件均为铁基材料,密度定义为7800 kg/m3,CT床主要部件材料及质量如表2所示。此外,由于病人几何形状及重量分布难以确定,分析时将其简化视为集中载荷处理。

表2 CT床主要部件材料及质量Tab.2 CT table main components’ material and quantity
2.3 边界条件与载荷的建立
病人的体型身高和平躺位置会影响CT床受力计算,本文假设病人重心位于床板端部距离L2处,病人重量为210 kg。在正常运行时CT床边界及载荷条件应包含公式(1)~(6),但长期运行后,空气弹簧可能出现磨损失效,此时模型边界及载荷条件设置为公式(1)~(5),仿真分析模型如图2所示,坐标原点为底座端点。

图2 CT床仿真分析模型Fig.2 CT table simulation analysis model

2.4 床架铰链位置优化模型
床架铰链位置的变化直接影响床体各铰链上的受力,选取最优的铰链位置可以有效降低铰链上的载荷。前面板为CT床的主要承载部件,因此以前面床板所有铰链平均值最小为优化目标,根据刚体动力分析的结果建立优化分析模型,并以当前设计参数L10=795 mm为变量初值。

3 仿真结果及分析
3.1 正常工况下各铰链及马达受力

图3 正常工况下铰链及马达受力Fig.3 Normal conditions hinges’ and motor’s force
图3 给出了CT床正常工作过程中,床体铰链及起升马达随床体位置变化的受力曲线。在整个运动过程中,最大铰链载荷为6.2 kN,位于起始时刻的C’铰链上,此时的马达载荷也为最大值8.2 kN。在床体起升的过程中,各铰链及马达上的受力呈降低趋势,且铰链C’、C和马达受力变化最为显著,其余铰链受力略有降低。当床体起升角为80o时,铰链C’、C和马达受力达到最小值且接近0。在床板伸出过程中,马达受力保持不变且几乎为0,各铰链受力随床板伸出长度呈线性增长且在床板伸出1600 mm都时达到最大值。此时,铰链D上载荷为5.2 kN,高于其他铰链受力。
3.2 空气弹簧失效时各铰链及马达受力
当空气弹簧同时失效时,所有驱动力由起升马达提供,此时铰链和马达受力如图4所示。图3和图4结果对比说明,空气弹簧的失效对铰链受力不产生影响,马达驱动力显著增大,最大值由8.2 kN增大到11.6 kN,且床板伸出阶段稳定值由0 N增大到4 kN。因此,空气弹簧的存在可以有效降低马达受力,同时马达最大承载能力需大于11.6 kN。
3.3 铰链位置优化对铰链及马达受力影响

图4 空气弹簧失效时铰链及起升马达受力Fig.4 Air spring failure hinges’ and lifting motor’s force

图5 铰链位置对铰链及马达最大载荷影响Fig 5 Hinge location of the hinge and motor load

图6 铰链位置对前面板整体受力的影响Fig.6 Hinge position on the front panel of the overall force
根据图5结果所示,马达载荷不受铰链位置变动的影响,铰链A,A’,B,B’,D和D’上的最大载荷随着铰链位置L1的增大呈线性增长趋势,铰链C’呈线性降低的趋势,而铰链C在L1=795 mm时有最小值。图6给出了前面板整体受力随铰链位置变化的曲线,结果表明随着铰链位置L1的增大,前面板整体受力呈抛物线变化趋势,在L1=795 mm时有最小值21.2 kN,因此当前设计铰链位置为最优位置。
4 设计参数的确定
4.1 轴承选型的确定
根据图3结果说明,铰链C’在CT床初始位置时承受载荷最大,负载为床体自重215 kg、病人重210 kg,当设计安全系数为4时:即床体自重215 kg、病人重840 kg,铰链最大受力简化计算为:
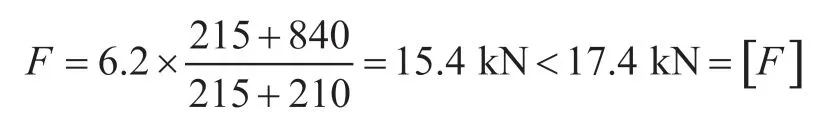
式中[F]为轴承许用载荷。
4.2 起升马达功率确定
根据设计要求,在空气弹簧全部失效时,马达仍能独立驱动床体升降,而过载工况中的床体载荷将由马达螺杆自锁来承受,因此根据图4结果,马达最低驱动力为11.6 kN,对应其功率为:

式中F为马达驱动力,V为驱动速度,f1为机械效率,f2为马达效率,n为安全系数
5 结论
本文借助COSMOS Motion 对CT床各种工况的全运动过程进行了仿真计算及铰链位置优化,根据计算得出以下结论:
(1)床体起始位置为最危险工况,且前铰链轴承选择满足4倍安全系数设计要求。
(2)双空气弹簧辅助支撑时可有效降低驱动杆的受力,在其同时失效时,马达驱动载荷也足以支撑床体。
(3) 当前上床体铰链处于最优位置,可以使前床板受力最低。
[1]尚洪,刘文志.CAE技术在CT产品研发中的应用[J].中国医疗器械杂志,2008,32(3):215-217.
[2]武超,高雪官,曹其新,等.带辅助运动平台的手术机器人设计与分析[J].医疗装备,2012,25(02):1-5.
[3]张晋西,郭学琴.SolidWorks及COSMOSMotion机械仿真设计[M],北京:清华大学出版社, 2007.

