吊重作业起重船波浪中的运动响应

汪娟娟，黄衍顺，李怀亮，谢维维

1 天津大学建筑工程学院，天津 300072

2 海洋石油工程股份有限公司，天津 300452

0 引 言

有关吊重作业起重船波浪中的运动响应研究，目前还没有非常成熟的成果［1］。Todd等［2］通过对起重船起吊重物进行实验、分析，得出起重船上吊杆起重机表现出经典的受迫球形摆的动力行为的结论，并提出起重船是典型的小阻尼系统，可以忽略系统的结构阻尼。Herry等［3］在研究起吊重物时，构建了由刚性无质量的吊索和一个吊重质点组成的起吊重物系统模型。Ren等［4］对起重船吊臂柔性对系统动力学特性的影响进行了分析，研究中使用的模型为二维平面钟摆模型。船舶高频运动会对起重机产生很大的附加载荷，吊绳悬挂的起吊重物在船舶摇摆的诱发下也会产生受迫振动，使起重作业的安全受到威胁，以至无法作业［5-6］。起重船以及吊重在海洋环境作用下可能出现的大幅摆动会降低吊装就位精度，增加吊重与其它结构碰撞的几率，对于工程作业而言，这都是很危险的［7-8］。

本文将运用三维势流理论建立起重船作业计算模型，对船体施行8点系泊。同时，建立吊重的质量矩阵，将吊重质点以吊绳与船体连接。考虑到实际海况，在时域计算中，引入风浪流海洋环境条件来计算起重船系泊状态下的运动响应。并将船体重心和吊重质心作为关键点，通过改变系泊缆预张力以及吊绳长度、吊重重量和吊距等起吊要素来分析这些要素对吊重运动及船体运动的影响，以及改变起吊要素，吊重摇摆与船体摇摆运动的相互影响。

1 基本理论

1.1 时域中辐射问题的势流理论

在线性化条件下，理论上可以求解满足相应边界条件和初始条件的非定常势函数。通过求解辐射流场的速度势函数，将运动浮体受到的水动力在正交直角坐标系中以分量的形式表达出来，如式（1）和式（2）所示［9］：

式中：Fj为作用于运动浮体的水动力在第 j个自由度上的分量；j为力分量的自由度( j=1，2，…，6 )；k为浮体运动分量的自由度(k =1，2，…，6)；μj，k为附连水质量系数，其中 j，k为定值时，表示浮体浸没部分的几何形状系数与时间无关；xk(t)为浮体第 j个自由度的位移，x¨k(t)为xk(t)对时间的两阶导数；Lj，k(t-τ)为自由液面记忆效应的时延函数；ρ为流体密度；P为流场中任意点的坐标。

1.2 频域中辐射问题的势流理论

频域中，分析浮体处于含有自由液面的理想流体中对流场产生的扰动的影响。当流场达到稳定状态时，流场存在满足拉普拉斯方程及满足边界条件的速度势函数，即 ϕ(P，t)= ϕ(P)e-iωt。

根据拉普拉斯方程定解条件，可利用格林函数法求解空间辐射速度势函数ϕj(P)，从而将运动浮体受到的水动力在正交直角坐标系中以分量的形式表达出来，如式（3）和式（4）所示［10］：

式中：μj，k为附连水质量系数；λj，k为阻尼系数，当 j，k为定值时，阻尼函数由浮体运动频率的函数决定。目前，附连水质量和阻尼系数既可以通过数值计算方法求得，也可以利用物理模型实验方法得到。

1.3 水动力在时域与频域中的转化

在线性化条件下，通过傅立叶变换来实现水动力由频域到时域的转化，如式（8）所示。

2 实例计算与结果分析

2.1 起重船基本数据

计算所需的基本数据如表1所示。

表1 计算基本参数Tab.1 Basic parameters

2.2 结果分析

实例计算中，风速取为31.8 m/s，流速取为1.08 m/s。

起重船纵向起吊，起重机布置在船尾，起重示意图如图1所示。

图1 起重示意图Fig.1 Abridged general view of hoisting

2.2.1 吊重的运动

本文以吊重重量2800.0 t，吊距41.66 m，波高1.5 m为例进行分析。由于船的横摇运动要比纵摇运动显著，而90°浪向下船的横摇运动最大，故选取90°浪向时吊重的摇摆运动进行分析。

实例计算中，吊绳的刚度取足够大，经计算对比，吊绳的轴向拉伸可忽略不计。计算的海况为规则波。

激励的前1000 s内，吊重的摇摆角度如图2～图5所示。

由图可知，吊重吊绳长度在36～66 m之间时，随着吊重吊绳长度的增加，Rx，Ry呈递增趋势，且Rx的增速要快于Ry。其中，Rx为吊重绕 x方向的摇摆角度，Ry为吊重绕y方向的摇摆角度。

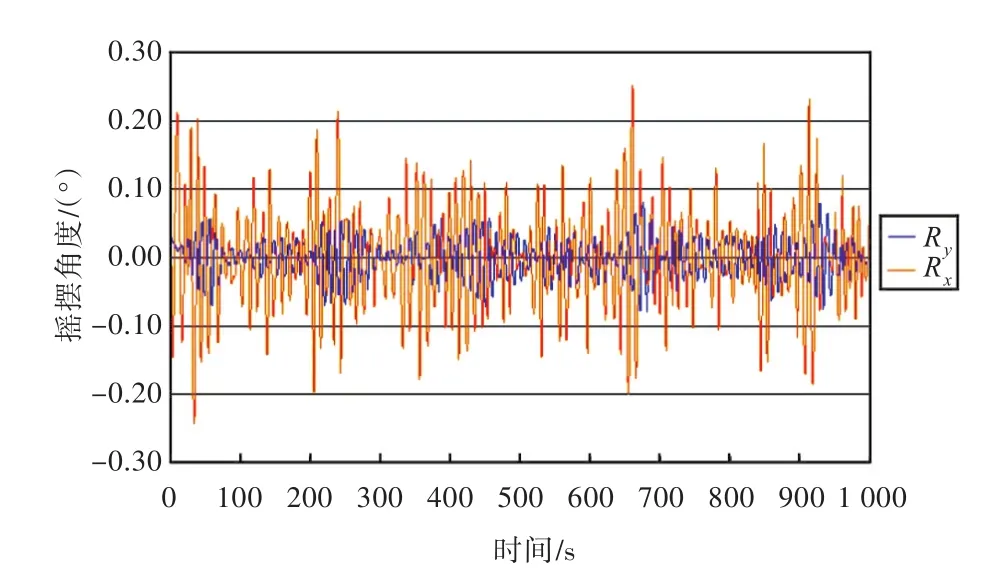
图2 吊绳36 m长时的吊重摇摆角度曲线Fig.2 Curves of the cargo swing angle with a 36 m lifting rope

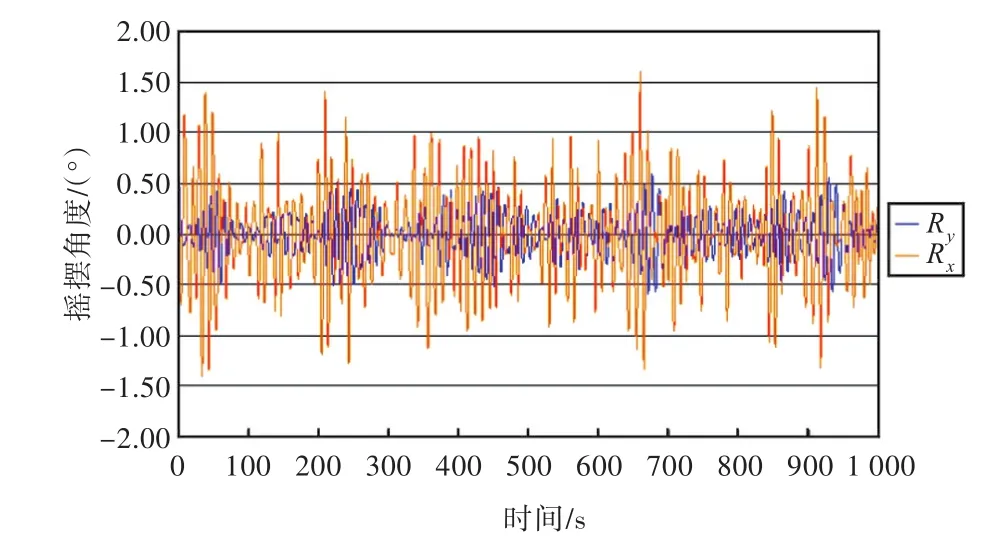
图3 吊绳46 m长时的吊重摇摆角度曲线Fig.3 Curves of the cargo swing angle with a 46 m lifting rope

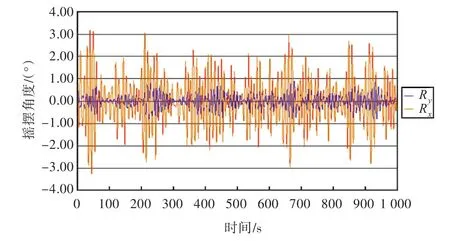
图4 吊绳56 m长时的吊重摇摆角度曲线Fig.4 Curves of the cargo swing angle with a 56 m lifting rope

图5 吊绳66 m长时的吊重摇摆角度曲线Fig.5 Curves of the cargo swing angle with a 66 m lifting rope

由于吊重摇摆的方向与空间上的摇摆幅值无法从数据上对应，所以只给出了xy矢量和方向摇摆的幅值，后面将对船与吊重摇摆运动的情况进行分析。吊重矢量和方向摇摆运动的幅值如图6～图9所示。

图6 吊绳36 m长时吊重矢量和方向摇摆幅值Fig.6 Sway amplitude of the cargo in vector direction with a 36 m lifting rope

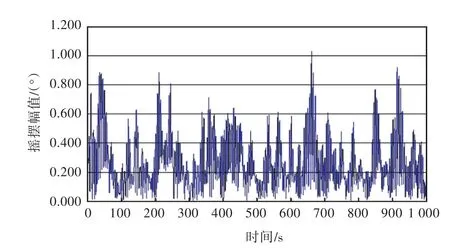
图7 吊绳46 m长时吊重矢量和方向摇摆幅值Fig.7 Sway amplitude of the cargo in vector direction with a 46 m lifting rope

图8 吊绳56 m长时吊重矢量和方向摇摆幅值Fig.8 Sway amplitude of the cargo in vector direction with a 56 m lifting rope

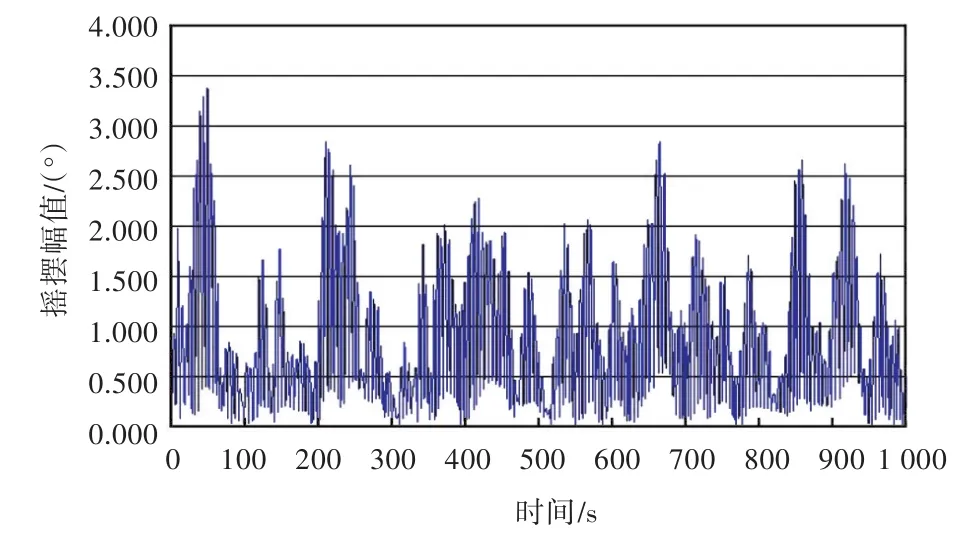
图9 吊绳66 m长时吊重矢量和方向摇摆幅值Fig.9 Sway amplitude of the cargo in vector direction with a 66 m lifting rope

由图中可看出，随着吊绳长度的增加，吊重本身单摆运动的固有周期增大，吊重摇摆幅值也加大，而幅值随时间的变化趋势则理论上不变。

2.2.2 相同吊重、吊距，不同吊绳长度时吊重与船摇摆运动的相互影响分析

由于吊重绕x方向的摇摆运动较大，所以主要分析这个方向的运动，绕y方向的摇摆运动只列出主要数据加以参考。

RAO为船舶运动的幅值响应算子。吊绳长度为36 m时，船的RAO曲线如图10和图11所示。

可以看出，此时船的固有横摇周期为13～15 s，固有纵摇周期为9～10 s。吊绳长度为46，56，66 m时，船的横摇、纵摇RAO曲线图几乎没有变化，受篇幅所限，此处不再列出。

在激励的前1000 s内，吊重与船的横摇运动如图12～图15所示。

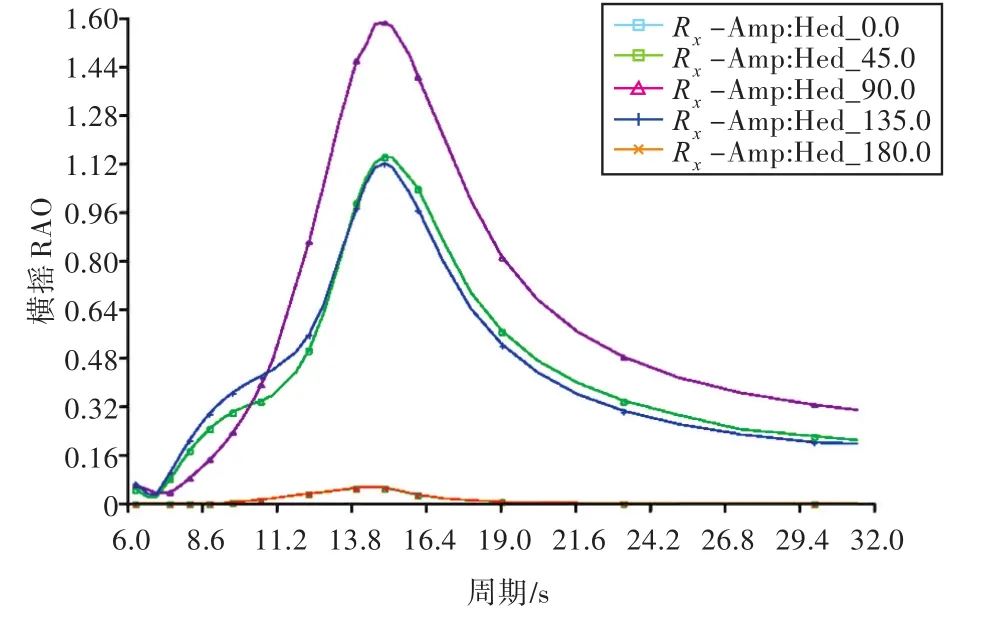
图10 船的横摇RAOFig.10 Ship's rolling RAO

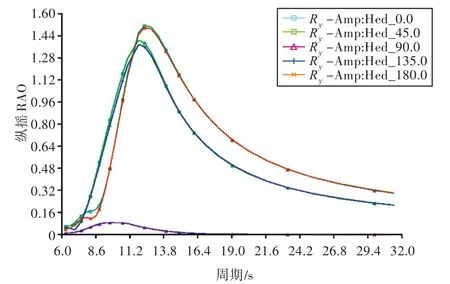
图11 船的纵摇RAOFig.11 Ship's pitching RAO

图12 吊绳36 m长时吊重与船的横摇运动对比Fig.12 Roll of cargo and ship with a 36 m lifting rope

图13 吊绳46 m长时吊重与船的横摇运动对比Fig.13 Roll of cargo and ship with a 46 m lifting rope

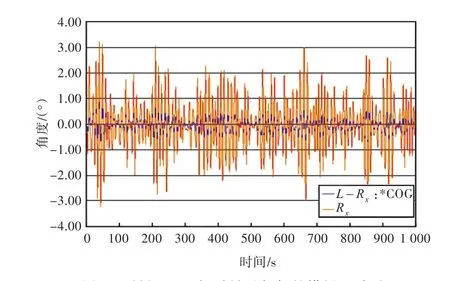
图14 吊绳56 m长时吊重与船的横摇运动对比Fig.14 Roll of cargo and ship with a 56 m lifting rope

图15 吊绳66 m长时吊重与船的横摇运动对比Fig.15 Roll of cargo and ship with a 56 m lifting rope

图中，L-Rx为船的横摇角度。随着吊绳长度的增加，吊重绕x方向的摇摆运动幅值也逐渐增加。当长度为56 m和66 m时，船的横摇运动幅值不同，但相位和周期较接近。

2.2.3 相同吊绳长度、吊距，不同吊重时吊重与船摇摆运动的相互影响分析

以40 m吊距，吊绳长47.1 m，波高1.5 m为例，分析吊重分别为1000，2800，4000 t时，前1000 s内的吊重摇摆幅值。船的RAO曲线如图16～图21所示。

图16 吊重1000 t时船的横摇RAOFig.16 Ship's rolling RAO with 1000 t cargo

图17 吊重1000 t时船的纵摇RAOFig.17 Ship's pitching RAO with 1000 t cargo

图18 吊重2800 t时船的横摇RAOFig.18 Ship's rolling RAO with 2800 t cargo

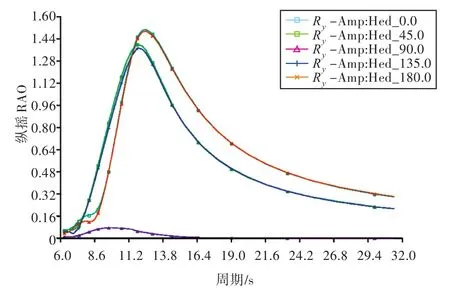
图19 吊重2800 t时船的纵摇RAOFig.19 Ship's pitching RAO with 2800 t cargo

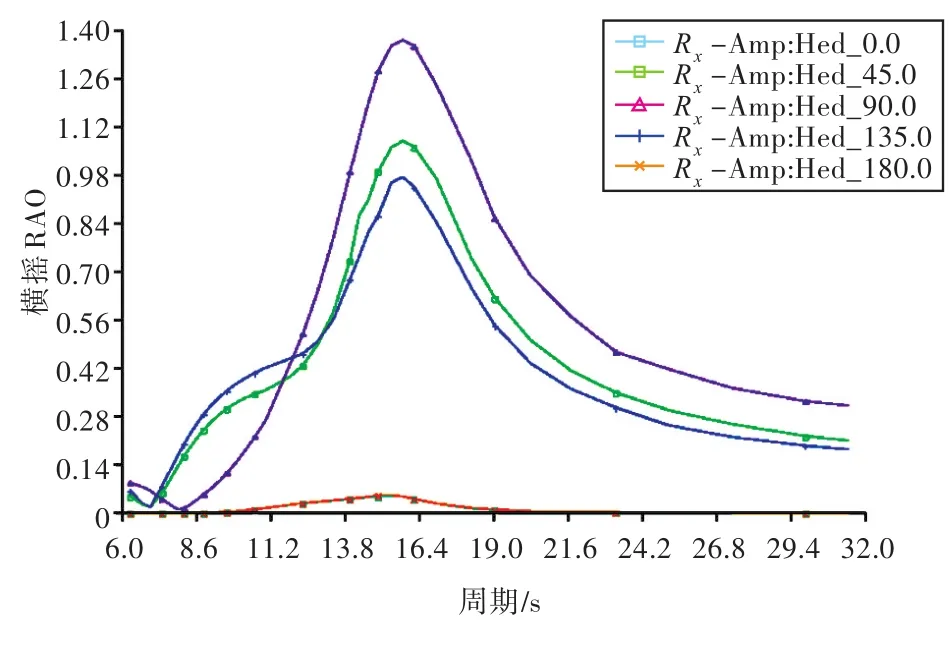
图20 吊重4000 t时船的横摇RAOFig.20 Ship's rolling RAO with 4000 t cargo

图21 吊重4000 t时船的纵摇RAOFig.21 Ship's pitching RAO with 4000 t cargo

此时，船的固有周期如表2所示。

表2 船的固有周期Tab.2 Ship's natural period

在激励的前1000 s内，吊重与船的横摇运动如图22～图24所示。

不同吊重重量下，起重船与吊重横摇运动幅值如表3所示。

由图表可看出，随着吊重重量的增加，船的横摇幅值和纵摇幅值均递减，但纵摇幅值变化不明显；吊重绕x方向和 y方向的摇摆幅值均减小，但绕y方向的摇摆幅值变化不明显。

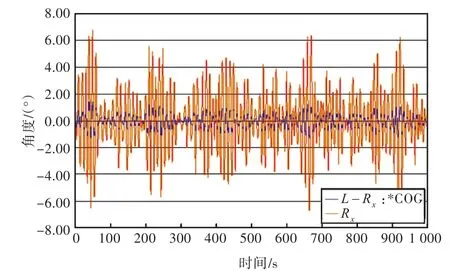
图22 吊重1000 t时与船的横摇运动对比Fig.22 Roll of cargo and ship with 1000 t cargo

图23 吊重2800 t时与船的横摇运动对比Fig.23 Roll of cargo and ship with 2800 t cargo

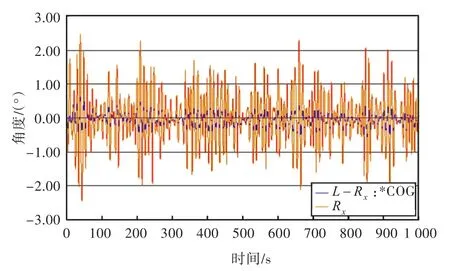
图24 吊重4000 t时与船的横摇运动对比Fig.24 Roll of cargo and ship with 4000 t cargo

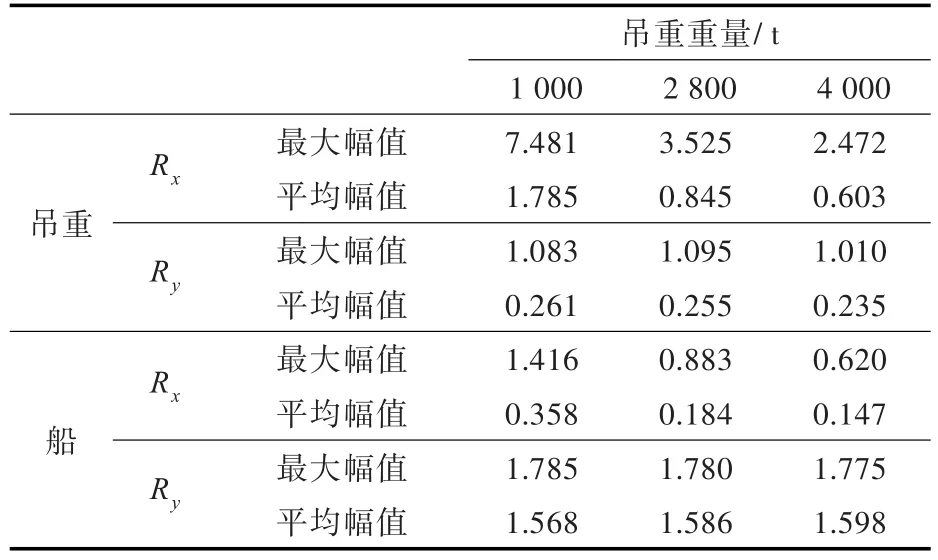
表3 不同吊重重量船与吊重横摇运动对比Tab.3 Roll of cargo and ship with different cargos

2.2.4 相同吊绳长度、吊重，不同吊距的吊重与船摇摆运动的相互影响分析

船的RAO曲线如图25和图26所示。

图25 船的横摇RAOFig.25 Ship's rolling RAO

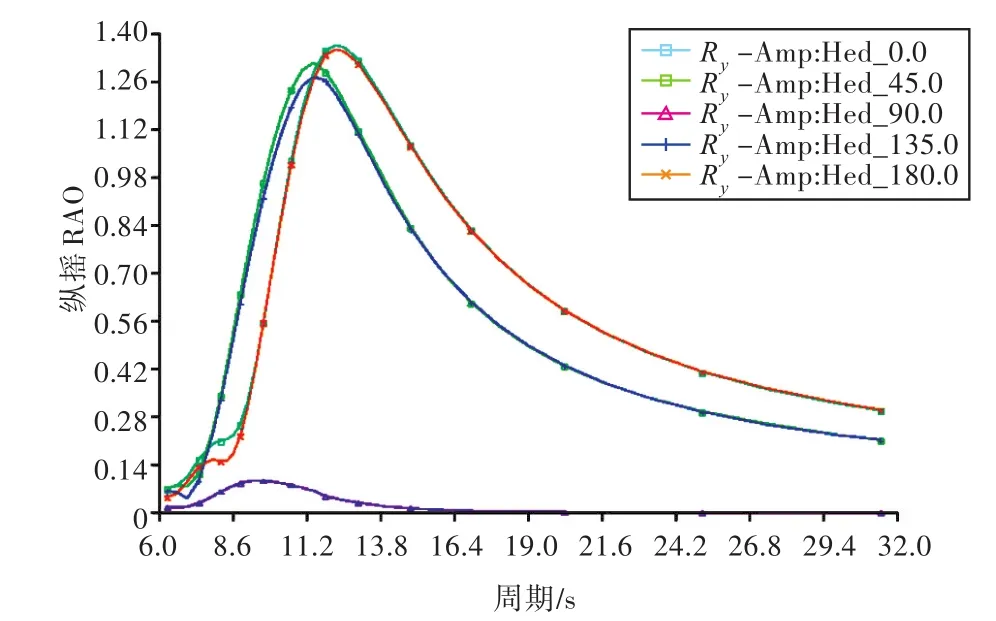
图26 船的纵摇RAOFig.26 Ship's pitching RAO

由图可看出，此时船的固有横摇周期为11～13 s，固有纵摇周期为9～10 s。当吊距为50，55，60 m时，船的横摇和纵摇RAO曲线图几乎没有变化，受篇幅所限，此处不再列出。

在激励的前1000 s内，吊重与船的横摇运动如图27～图30所示。

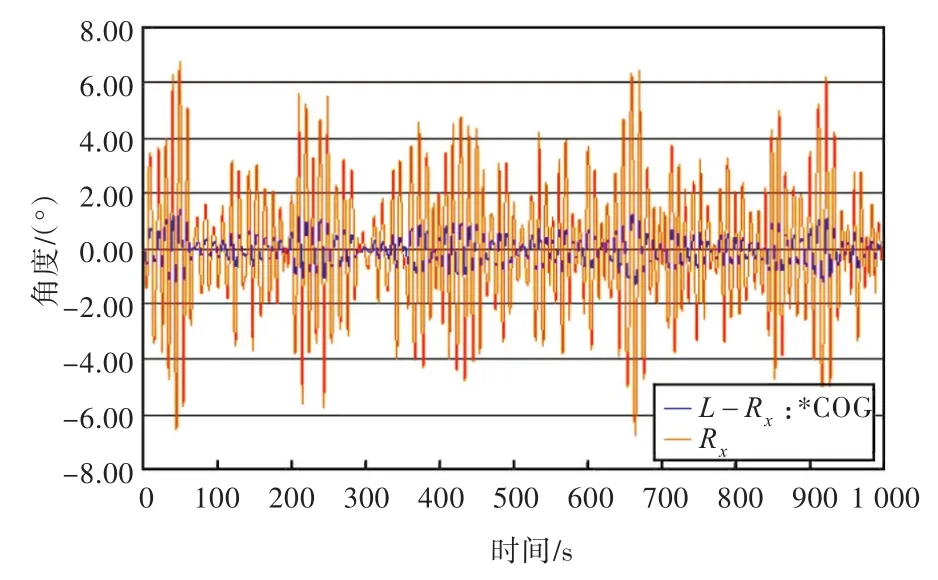
图27 吊距45 m时吊重与船的横摇运动对比Fig.27 Roll of cargo and ship with 45 m lifting distance

不同吊距下，起重船与吊重横摇运动幅值如表4所示。

表4 不同吊距船与吊重横摇运动对比Tab.4 Roll of cargo and ship with different lifting distances

由图表中可看出，随着吊距的增加，船的横摇幅值递增，但增量很小；而纵摇幅值则几乎没有变化。吊重绕x方向及 y方向的摇摆幅值均增加，但增量很小。由此可见，改变吊距对船及吊重的摇摆运动的影响不大，吊距不是个敏感因素。

在本算例中，谱峰周期约为10 s，MOSES频域分析的结果表明，横摇与纵摇固有周期均较接近于谱峰周期，因此易受海浪的影响。

3 结 论

本文对起重船在波浪中系泊状态下的运动响应进行了研究。在时域计算中，引入了风浪流海洋环境条件，以船体重心和吊重质心为关键点，通过改变系泊缆预张力及起吊要素，分析了不同浪向、吊重吊绳长度、吊重和吊距情况下，吊重运动及船体运动的变化情况，得到如下主要结论：

1）当吊绳长度在36～66 m之间时，随着吊绳长度的增加，Rx，Ry呈递增趋势，且Rx的增速要快于Ry。随着吊绳长度的加大，吊重本身单摆运动的固有周期加大，吊重摇摆幅值也加大，而幅值随时间的变化趋势理论上则没有改变。

2）随着吊重重量的增加，船的横摇幅值和纵摇幅值均递减，但纵摇幅值变化不明显；吊重绕x方向及 y方向的摇摆幅值均减小，但绕 y方向的摇摆幅值变化不明显。

3）随着吊距的增加，船的横摇幅值递增，但幅值增量很小，而纵摇幅值则几乎没有变化。吊重绕x方向和 y方向的摇摆幅值均增加，但增量很小。由此可见，改变吊距对船及吊重的摇摆运动影响不大，吊距不是敏感因素。

［1］CHIN C，NAYFEH A H，ABDEL-RAHMAN E.Non-linear dynamics of a boom crane［J］.Journal of Vibration and Control，2001，7（2）：199-220.

［2］TODD M D，VOHRA S T，LEBAN F.Dynamical measurements of ship crane load pendulation［C］//Oceans'97 MTS of IEEE Conference Proceedings，1997：1230-1236.

［3］HERRY R J，MASOUD Z N，NAYFEH A H，et al.Cargo pendulation reduction of ship-mounted cranes via boom-luff angle actuation［J］.Journal of Vibration and Control，2001，7（8）：1253-1264.

［4］REN H L，WANG X L，HU Y J，et al.Dynamic response analysis of moored crane-ship with a flexible booms［J］.Journal of Zhejiang University Science A，2008，9（1）：26-31.

［5］POSIADALA B.Effect of vibration in hoist system on dynamics of truck crane［J］.Zeitschrist fur Angewandte Mathematik und Mechanik，1996，76（S5）：403-404.

［6］王赣城，金长明，陈云文.吊杆式船载起重机吊绳非线性动力学建模与分析［J］.噪声与振动控制，2010（2）：23-27.Wang Gancheng，Jin Changming，Chen Yunwen.Nonlinear dynamic modeling and analysis of cable in boom ship-mounted crane［J］.Noise and Vibration Control，2010（2）：23-27.

［7］董艳秋，韩光.起重船吊物系统在波浪中的动力响应［J］.中国造船，1993（1）：64-71.DONG Yanqiu，HAN Guang.Dynamic response of lifting load system of crane vessel in waves［J］.Shipbuilding of China，1993（1）：64-71.

［8］SARKAR A，TAYLOR R E.Dynamics of mooring cables in random seas［J］.Journal of Fluids and Structures，2002，16（2）：193-212.

［9］余建星，董文斌，戴愚志.RMFC模型在新型拼接式海上栈桥码头三维运动响应计算中的应用［J］.港工技术，2006（4）：1-4.YU Jianxing，DONG Wenbin，DAI Yuzhi.The application of RMFC model in the three-dimensional motion response calculation of new concatenation type maritime quay of landing stage［J］.Port Engineering Technology，2006（4）：1-4.

［10］唐友刚.海洋工程结构动力学［M］.天津：天津大学出版社，2008：43-72.