运输机空投飞行载荷分析

侯宗团, 荆志伟, 郭兆电

(西安飞机设计研究所 总体气动设计研究所, 陕西 西安 710089)

运输机空投飞行载荷分析

侯宗团, 荆志伟, 郭兆电

(西安飞机设计研究所 总体气动设计研究所, 陕西 西安 710089)

为了对军用运输机空投时的飞机响应进行分析与评估,给飞行载荷和操稳设计提供基本依据,将飞机与货物视为一个整体系统,建立空投过程中载机与货物的动力学方程;根据《军用飞机结构强度规范》中的空投和空投阵风准则进行了仿真计算,给出了空投过程中飞机的动响应与部件载荷时间历程。仿真结果表明,所提供的方法能够满足运输机空投时的飞行载荷分析要求。

空投; 阵风; 飞行载荷; 动响应

0 引言

运输机在货物空投过程中会发生一系列的变化:(1)飞机的质心位置和转动惯量发生变化,在货物出舱瞬间,这些参数和全机质量将会突变;(2)投放前飞机处于配平状态,投放后平衡状态破坏;(3)引起飞机运动参数和各部件的气动载荷与惯性载荷变化。这些变化可能会对飞机的运动特性、结构强度及飞行安全产生不利影响。

针对运输机空投,GJB 67.2A-2008 《军用飞机结构强度规范》对空投拉起机动和空投滚转机动做了相关要求,并阐述了空投阵风准则。美国国防部联合使用规范指南JSSG-2006 《飞机结构》对空投亦进行了详细的描述:空投和投放准则使用1g飞行假设,飞机配平到大约2°的迎角;投放使用0.25g的引出加速度;将1-cos型、7.62 m/s的离散阵风叠加到空投情况上,以使当货物处于投放边缘时产生结构峰值响应。

因此根据规范要求,需要进行运输机空投动响应计算分析,确定空投载荷,供强度部门分析使用,以确保货舱地板、货桥、后机身、平尾等部件在货物空投过程中的结构安全和飞机的飞行安全。

国内在运输机空投动响应方面已有较多研究,成果主要集中在飞机的飞行品质方面,并且动力学方程的建立基本是将载机与货物分为两部分进行[1-2]。本文将载机、货物视为一个整体系统,进行空投动力学建模,计算分析了相关部件的载荷,为结构强度设计提供依据。由于空投拉起和空投滚转仅是空投构型下的机动,并不投放货物,和常规的拉起机动和滚转机动类似,故本文不再阐述。本文仅对货物空投过程中飞机遭遇1-cos型垂直阵风进行研究,无阵风情况与之类似。

1 动力学建模

1.1 基本定义与假设

空投过程涉及两个对象:被投货物称为货物,不含货物的飞机称为载机。货物和载机合称为全机。

本文将载机、货物视为整体系统,以本系统的瞬时质心作为参考点,建立空投过程中飞机与货物系统的运动方程。全机体轴系的原点O为全机的瞬时质心,Ox轴在飞机对称面内,平行于机身构造水平面,指向前;Oz轴在飞机的对称面内,指向下;Oy轴垂直于飞机的对称面,指向右。图1为全机体轴系示意图,图中A点为载机自身质心位置,C点为货物质心位置。

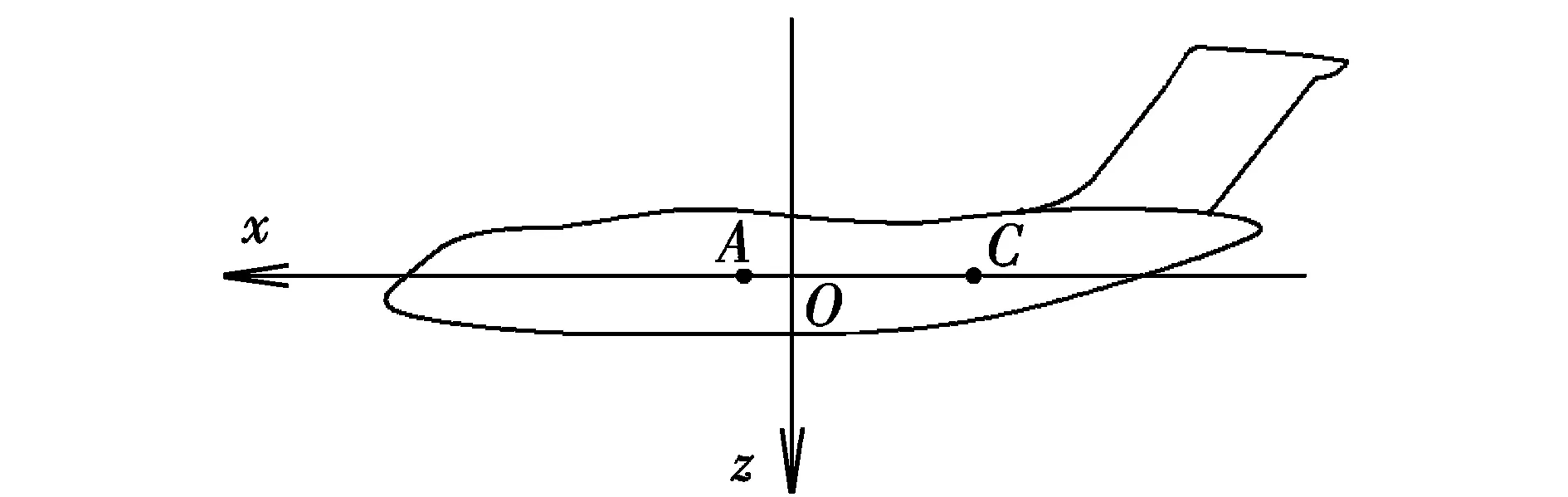
图1 全机体轴系示意图Fig.1 Coordinate axes of the aircraft body

为便于建立数学模型,作以下基本假设:(1)采用“平面地球假设”,且忽略地球的自转;(2)货物可看成具有集中质量的质点;(3)货物在脱离载机之前始终被约束在货舱地板上;(4)货物在舱内做匀加速运动,并且货物的质心位于载机的对称面内;(5)忽略货物出舱对飞机气动特性的影响。

1.2 全机动力学模型

本文飞机质心动力学方程与传统的飞机质心动力学方程形式一致,体轴系下的质心动力学方程为:

(1)

(2)

式中,m为载机与货物的质量和,当货物脱离载机后,m为载机的质量;u,w分别为飞机质心速度在体轴系x轴和z轴上的分量;α为飞机迎角;θ为飞机俯仰角;q为机体的俯仰角速度;φ为发动机安装角;T为发动机推力;D,L分别为飞机的阻力和升力;g为重力加速度。

下面推导全机绕质心转动的动力学方程。全机对质心O的动量矩为:

GOy=JOyq

(3)

式中,JOy为全机对移动机体质心坐标系的俯仰惯性矩,是一个时变参量,当货物脱离载机后,JOy不计货物影响。

将式(3)代入动量矩方程,整理得:

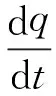
(4)

式中,MOy为气动力和推力对瞬时质心O的俯仰力矩。

根据货物在货舱内的运动规律,可以得到:

(5)

(6)

(7)

根据式(1)、式(2)和式(4),再补充飞行力学中的相关运动方程、几何方程及关系式,即可进行空投动响应计算。

1.3 气动迎角修正

根据式(1)、式(2)、式(4)及相关方程,可以求出全机质心处速度VO的大小和方向。由于全机质心在变动,质心的速度VO并不准确地等于机体相对于大气的速度Vt,会引起气动迎角的计算误差,因此需要进行速度换算,求解机体的真实气动迎角。

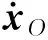
(8)

运用正弦、余弦定理和小扰动理论,可得到真实的气动迎角为:

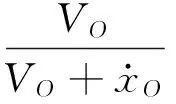
(9)

式中,α为由质心动力学方程得到的气动迎角,由式(10)确定。

(10)

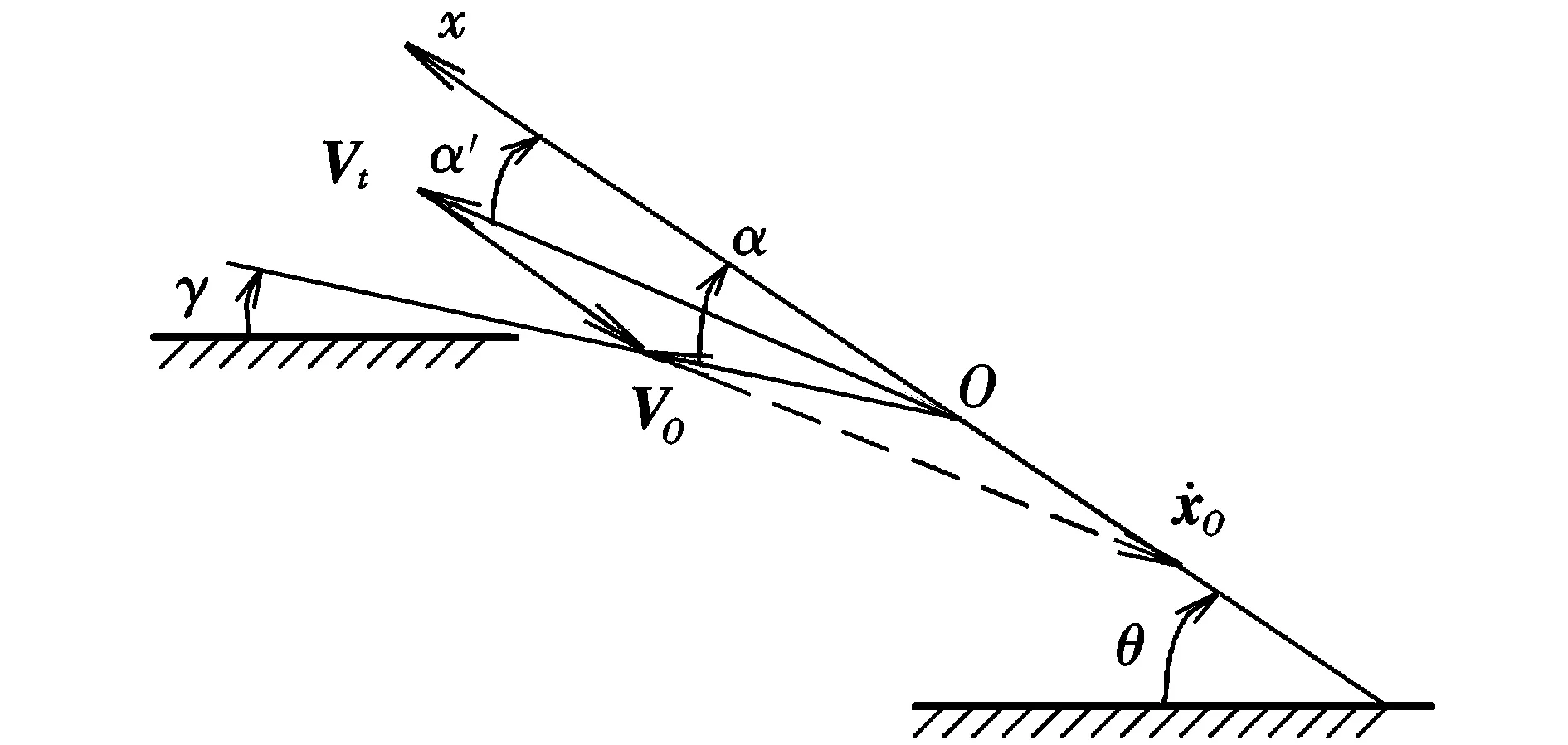
图2 真实机身迎角修正示意图Fig.2 Correction of the angle of attack

1.4 离散阵风动响应

为满足空投离散阵风准则的设计要求,引入满足设计规范的阵风激励。在飞行品质评定、飞行载机设计中,广泛采用1-cos型阵风模型,其风速剖面如图3所示。该阵风模型为:

(11)

式中,xg为飞机位置;wg0为阵风速度;Lg为阵风尺度。

图3 “1-cos”型离散阵风模型Fig.3 ‘1-cos’gust model

运输机空投动响应分析过程中,需将1-cos型阵风合理地叠加至全机运动学方程的求解过程中,并满足当货物运动至货桥边缘时,阵风恰好达到最大强度。这样可以使飞机结构产生峰值响应,达到空投阵风载荷的设计边界。

1.5 货物对载机的作用力

由于货物出舱速度较高,哥氏(Coriolis)效应对货桥的卸载是显著的,在货桥和货舱地板载荷设计过程中,应该考虑货物对货桥和货舱地板的哥氏作用力。货物对载机的法向作用力为:

(12)

2 数值仿真

2.1 计算模型

货物空投仿真参数如表1所示。为了确定飞机在空投货物时的边界设计载荷,算例飞机均处于开环状态,没有引入纵向增稳控制系统。

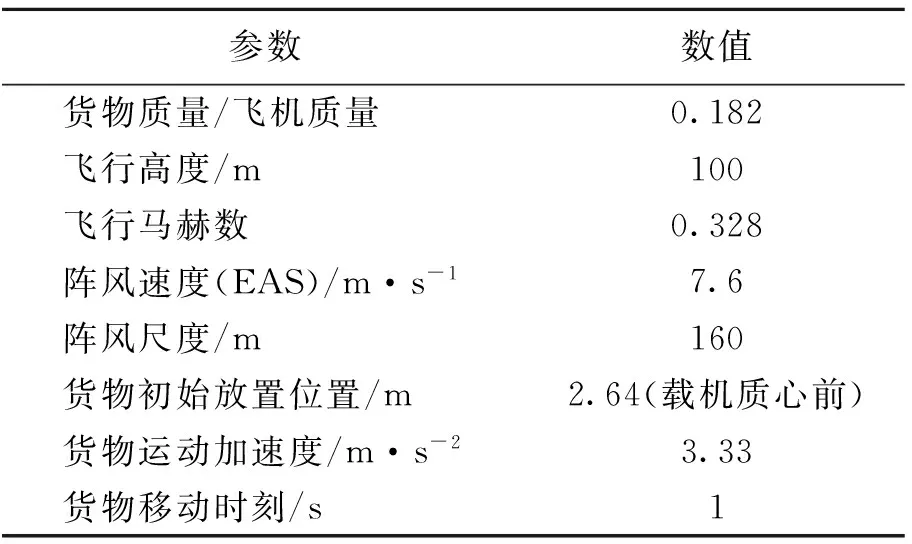
表1 货物空投仿真参数Table 1 Simulation parameters of airdrop

2.2 飞机空投动响应分析

2.2.1 配平分析

根据表1所给的货物空投仿真参数,对货物投放前进行配平分析,得到飞机1g平飞的配平结果:机身迎角为4.449°,平尾偏角为-2.755°。

2.2.2 投放动响应分析

根据表1所给空投仿真参数,以上述配平结果作为空投动响应求解初始条件,飞机空投动响应如图4～图10所示。

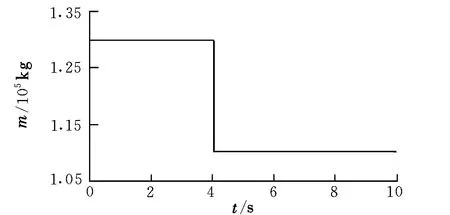
图4 全机质量时间历程Fig.4 Mass-time history of the whole aircraft

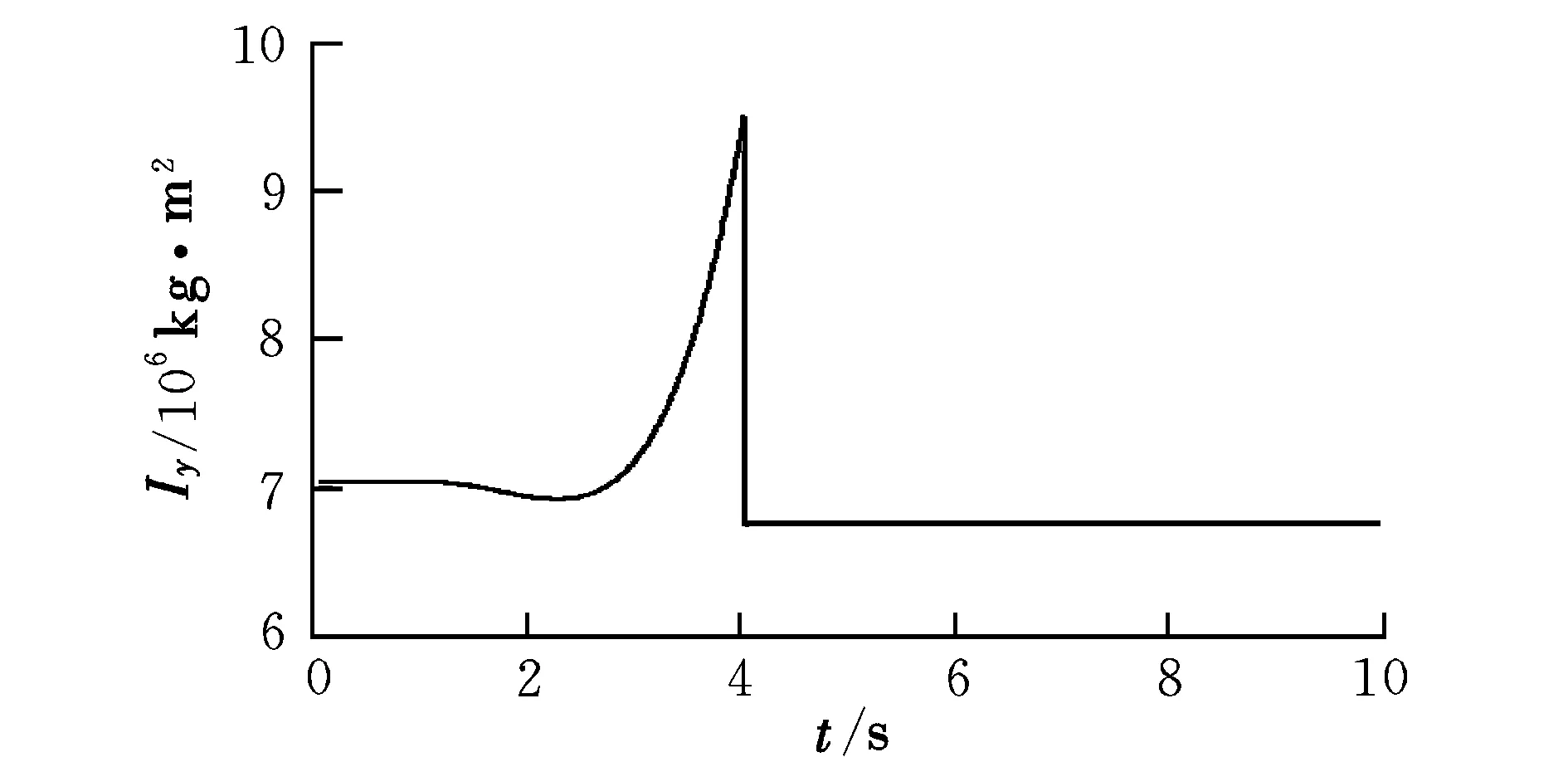
图5 全机绕质心俯仰转动惯量时间历程Fig.5 Time history of the aircraft pitch inertia

图4和图5为全机质量特性时间历程。在货物从前向后至货舱门移动过程中,当货物处于载机质心前时,全机绕质心的俯仰转动惯量略有降低;当货物移动至载机质心后,全机绕质心的俯仰转动惯量一直增加;直至货物脱离载机,全机的质量特性发生突变,全机的质量变为载机自身质量,全机绕质心的俯仰转动惯量变为载机绕自身质心的俯仰转动惯量。

图6和图7分别为俯仰角加速度和俯仰角速度时间历程。随着货物向后移动,货物对全机产生一个持续增加的抬头力矩,使得俯仰角加速度持续增加,进而引起俯仰角速度逐渐增加;货物脱离载机瞬间,飞机质心回到载机质心,而飞机迎角来不及变化,载机受到一个较大的低头气动力矩,俯仰角加速度瞬间变为负值,随即俯仰角速度也逐渐降低。

图6 俯仰角加速度时间历程Fig.6 Dynamic response of pitch angular acceleration

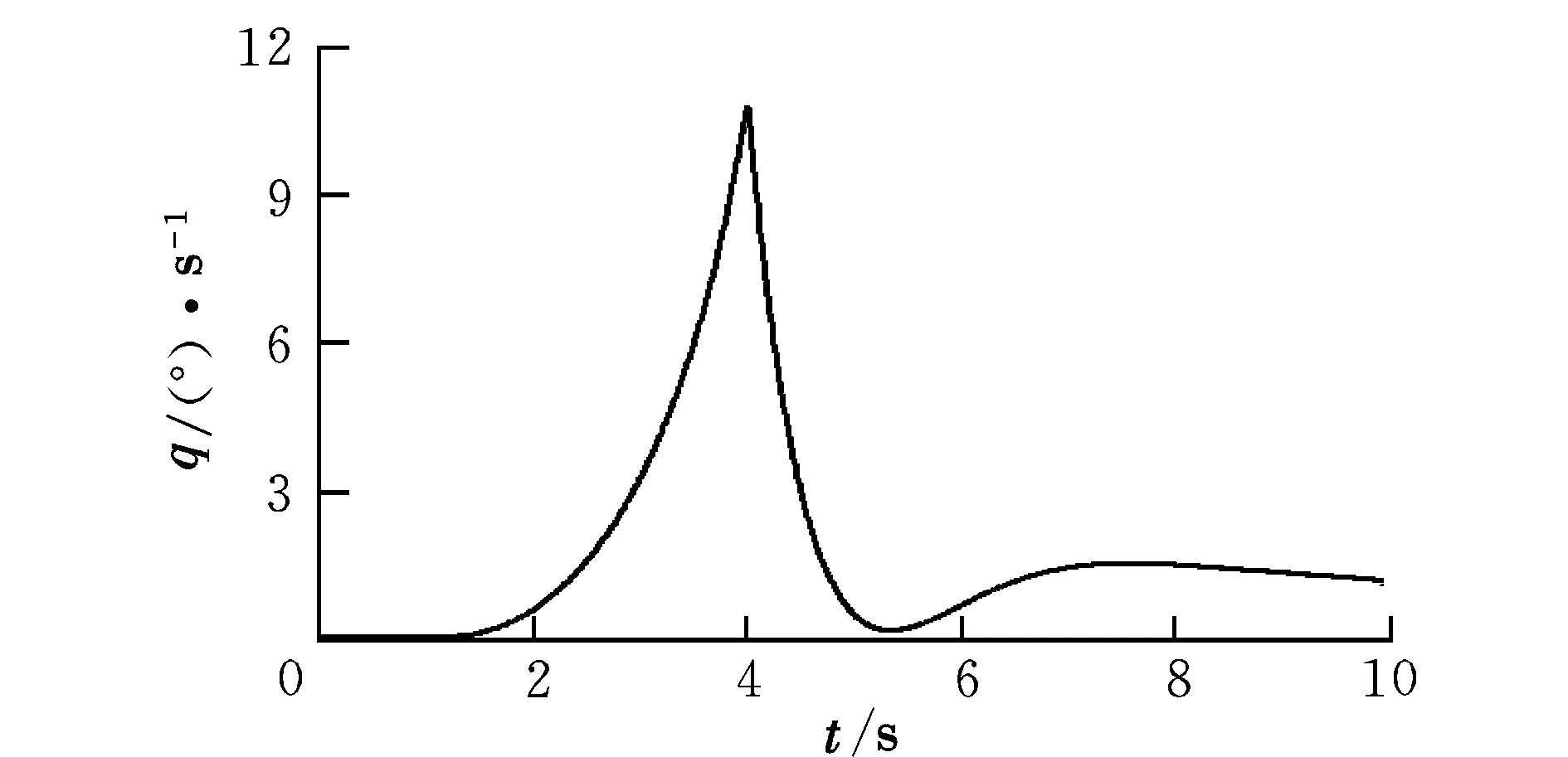
图7 俯仰角速度时间历程Fig.7 Dynamic response of pitch rate

图8为机身迎角时间历程。在货物向后移动的过程中引入阵风激励,机身迎角先迅速增加,然后降低,最终稳定在比配平迎角略大的状态。

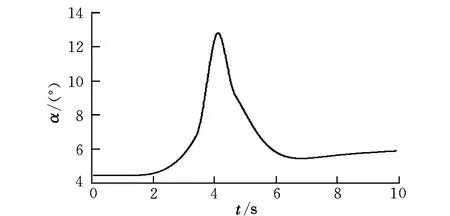
图8 机身迎角时间历程Fig.8 Dynamic response of angle of attack

图9为全机法向载荷系数时间历程。在t=4 s时,全机的法向载荷系数有一个约为0.4的阶跃增量,这是由于货物脱离载机瞬间,全机的气动力来不及变化造成的。

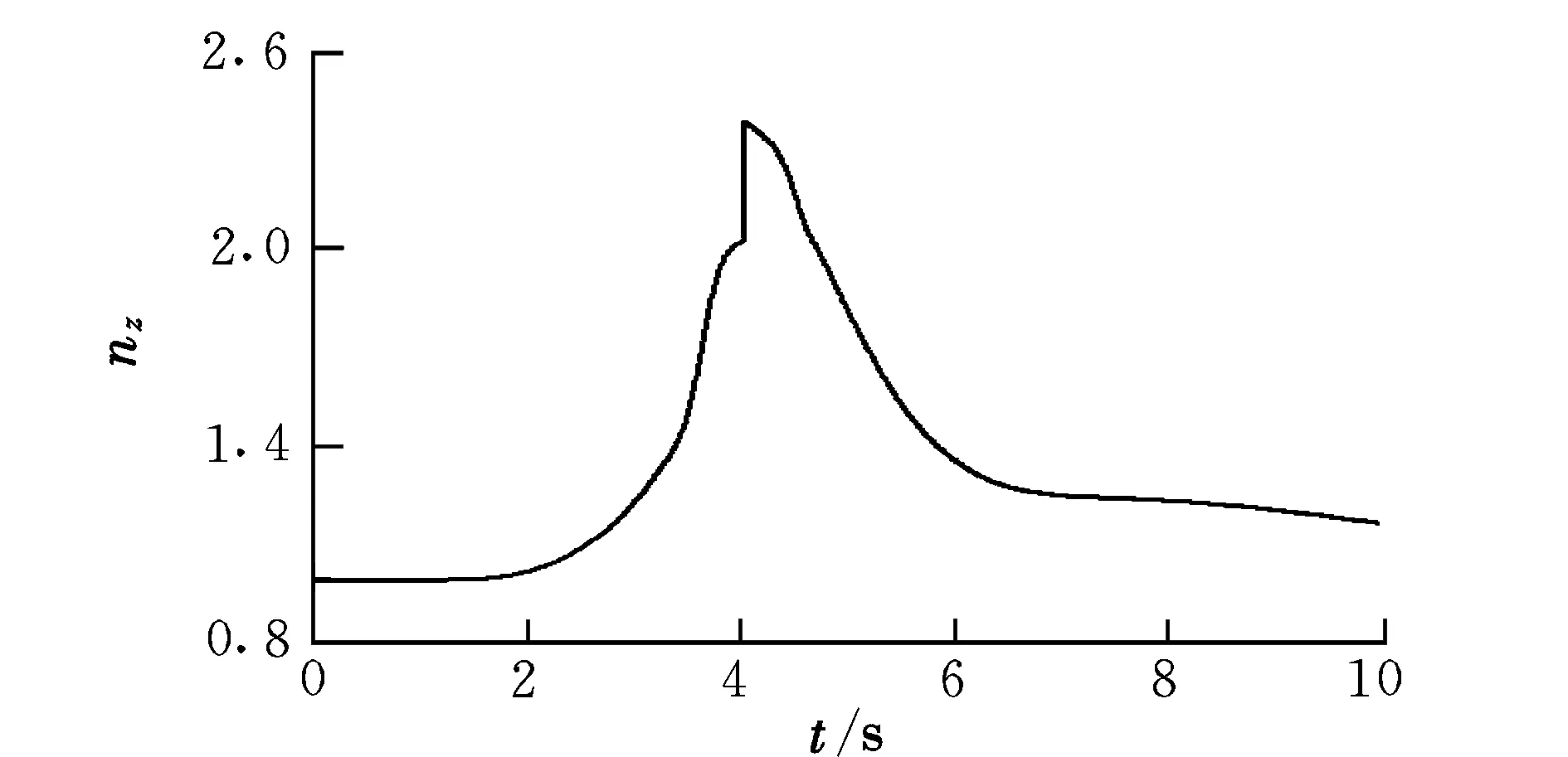
图9 全机法向载荷系数时间历程Fig.9 Dynamic response of the aircraft normal load factor

图10为平尾法向力时间历程。平尾的配平法向力向下,随着货物向后移动,机身迎角增大,平尾的法向力方向变为向上;当货物脱离载机后,机身迎角降低,最终稳定在比配平迎角略大的状态,平尾的法向力稳定在一个较小的正值状态。

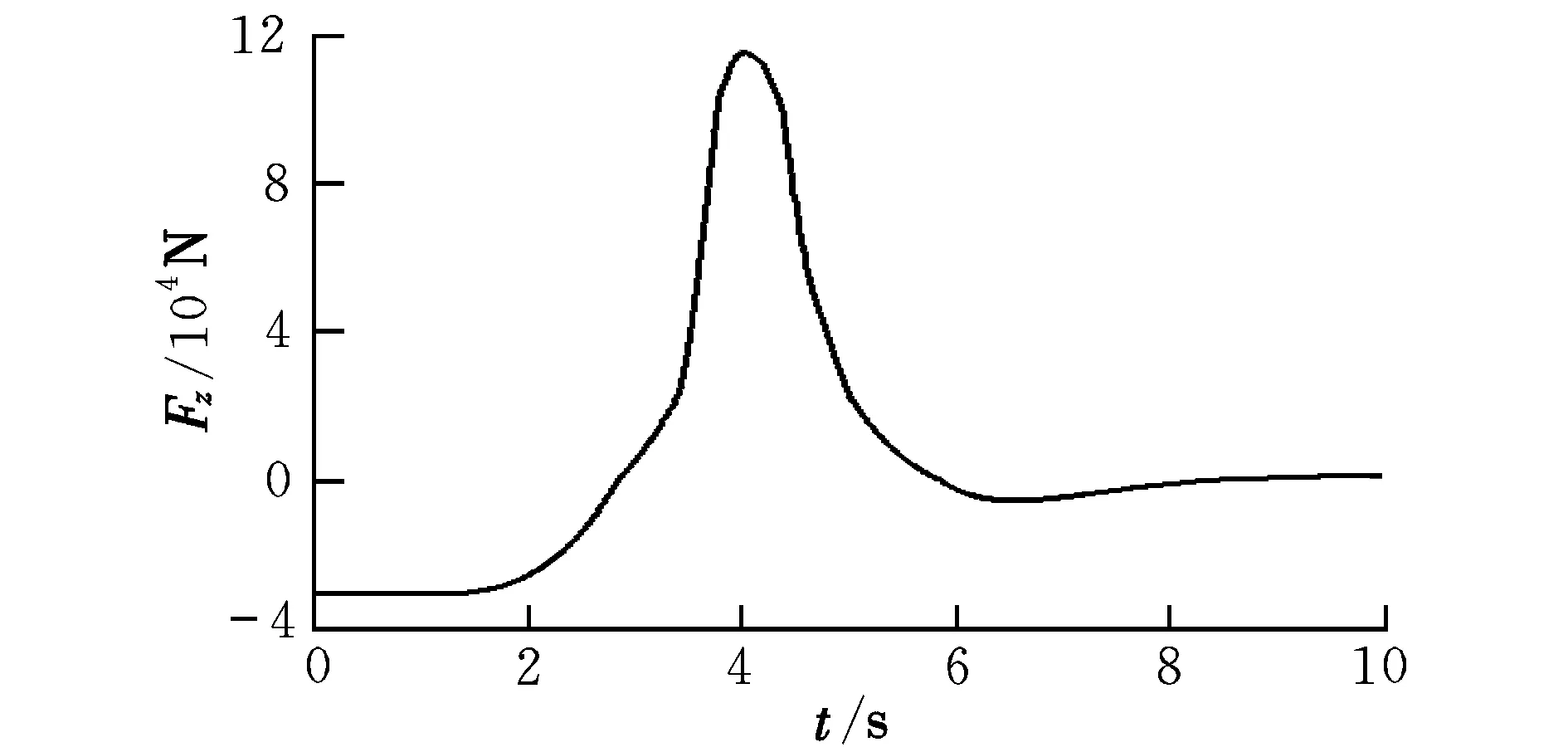
图10 平尾法向力时间历程Fig.10 Dynamic response for normal force ofthe horizontal tail

根据飞机运动参数、货物的质量特性和货物的运动规律,可以求得货物对载机的作用力,如图11所示,从图中可以看出哥氏效应的卸载效果是显著的。

图11 货物对载机的法向作用力Fig.11 Normal force of the cargo on aircraft

3 结束语

空投是规范要求的一种载荷设计情况,关系着飞机的结构安全和飞行安全。本文将载机、货物视为整体系统,建立了动力学方程,按照规范要求叠加离散阵风,进行飞机空投动响应仿真,数值结果规律良好,数值量级合适。在真实的空投过程中,飞机可能会打开纵向增稳控制系统或者由飞行员操纵飞机,确保飞机高度、姿态等变化不剧烈,亦可起到载荷减缓作用。本文尚未考虑控制系统对飞机空投动响应的影响,在今后的工作中有必要进行研究。

[1] 甘欣,朱江.空投时飞行品质的研究[J].飞机工程, 2009, (4):13-16.

[2] 杨妙升,屈香菊.运输机空投的飞行动力学建模及仿真[J].飞行力学, 2010,28(3): 9-12.

Analysisofflightloadsfortransportaircraftairdrop

HOU Zong-tuan, JING Zhi-wei, GUO Zhao-dian

(General Configuration and Aerodynamic Design Institute, Xi’an Aircraft Design Institute,
Xi’an 710089, China)

Aircraft’s dynamic responses of cargo airdrop should be analyzed and evaluated in detail so as to supply the design basis for the flight loads and handling quality design. Taking the aircraft and cargos as an integrated system, the dynamic equation for the aircraft and cargos during airdropping was established for analysis and evaluation of aircraft response in the case of airdrop by military transport aircraft and providing the design basis for flight loads and handling quality. The simulation was conducted according to the airdrop and airdrop gust guidelines which are described in theMilitaryAircraftStructureandStrengthSpecification. The aircraft’s dynamic responses and component’s dynamic loads during airdrop were demonstrated. Simulation results indicate that the method meets the requirements for flight loads analysis of transport aircraft airdrop.

airdrop; gust; flight loads; dynamic response

V212.1

A

1002-0853(2013)05-0416-04

2012-12-27;

2013-06-13; < class="emphasis_bold">网络出版时间

时间:2013-08-21 16:15

侯宗团(1971-)，男，陕西乾县人，高级工程师，研究方向为飞行载荷设计与分析；荆志伟(1984-)，男，河南郑州人，工程师，研究方向为飞行载荷设计与分析。

(编辑：李怡)