作战飞机翼面损伤对其气动特性的影响研究
高玉伟, 韩庆, 张锋,刘星
(1.西安飞机设计研究所 结构设计研究所, 陕西 西安 710089;2.西北工业大学 航空学院, 陕西 西安 710072)
作战飞机翼面损伤对其气动特性的影响研究
高玉伟1, 韩庆2, 张锋2,刘星2
(1.西安飞机设计研究所 结构设计研究所, 陕西 西安 710089;2.西北工业大学 航空学院, 陕西 西安 710072)
作战飞机易损性分析是其生存力设计与评估的基础问题之一。参考某型战机实弹打击试验结果,分别建立了该机在破片、离散杆和连续杆战斗部打击下的三种典型损伤模型,基于N-S方程数值模拟的方法计算该机在受损前后的纵向气动特性。对连续杆战斗部所造成的切断损伤,进一步研究了纵向配平问题。研究结果表明,相对于破片和离散杆战斗部,连续杆战斗部造成的损伤对其气动影响更为显著,甚至可能导致飞机在特定状态下的杀伤。研究结果可用于战损飞机杀伤准则的判定。
作战飞机; 易损性; 战斗部; 气动特性
0 引言
飞机作战生存力(ACS)定义为:“飞机躲避和承受人为敌对环境的能力”[1-2],因此生存力可分为两部分:敏感性和易损性。传统的易损性研究对象仅限于飞行员、燃油、发动机等关键部件的损伤情况[3],而对于战损引起的飞机气动特性变化以及这一变化对飞行基本功能的影响,目前国内外研究较少。
通过某型战机的易损性实弹打击试验可知,该机被不同导弹战斗部击中后,会在机体表面产生大量不同形状的穿孔破损和机翼部分切断损伤,但这些损伤并不一定会造成飞行员、发动机、油箱等关键部件的杀伤。
本文在飞机关键部件未杀伤的前提下,从空气动力学的角度研究这些表面损伤对其纵向气动特性的影响及其配平问题,以评价战损飞机保持基本飞行功能的能力。
1 计算模型及计算方法
1.1 计算模型
根据该飞机易损性实弹打击试验结果,基于该飞机的无损模型,如图1所示,分别建立了破片、离散杆和连续杆[4-5]三种比较典型的杀伤元造成的损伤模型。

图1 计算模型Fig.1 Calculation model
由图1(b)可知,破片是按弦向与展向等比例分配于机翼上的,且对机翼造成的损伤形式为穿透机翼损伤。由于离散杆损伤模型与破片损伤模型比较相似,也是按弦向与展向等比例分配的,仅损伤形状和大小有所不同,所以未给出其损伤模型图。破片穿孔的直径为40 mm,杆条穿孔的尺寸为12 mm×105 mm。对于连续杆造成的损伤,假设其作用于机翼上,沿弦向靠近翼尖并呈线性分布,且打掉了该线性分布靠近翼尖部分的机翼,如图1(c)所示。由于连续杆打掉了部分机翼,引起该飞机的参考面积发生了变化;所以,相关气动参数的计算均以变化后的面积为参考面积。
1.2 计算网格
计算网格采用六面体结构化网格[4],对应无损模型和连续杆损伤模型,其网格量大约为400万,如图2(a)所示。对于破片和离散杆损伤模型,由于损伤附近需要加密,网格量猛然增加到大约1500万,图2(b)为破片损伤的局部网格[5],由该图损伤处的局部放大图可明显看出破片打穿了机翼。由于网格的相似性,因此未给出离散杆和连续杆损伤的网格图。

图2 计算网格Fig.2 Computational grid
由于网格差异容易引起计算误差,因此对于每个模型,均采用同一套网格拓扑结构,且仅对损伤部位进行了局部加密处理。对于破片和离散杆造成的穿透损伤,在其损伤内部生成内“O”,以便气流通过。
考虑到真实的飞行环境,本文对整个飞机生成外“O”以模拟其附面层[6]流动,图2(c)为该飞机的对称面网格。对于附面层的设置,假设第一层厚度为cA×10-5,相邻两层厚度的比率为1.2。
1.3 计算方法
采用三维可压缩非定常N-S方程的积分形式进行数值模拟,其通式在直角坐标系中可表示为:

(1)
式中,各变量的具体定义见文献[7]。计算中采用格心格式的有限体积法对控制方程进行离散,湍流模型采用SSTk-ω模型,该湍流模型能够较准确地模拟分离流、漩涡流等复杂流动现象[8]。
计算中涉及的边界条件有远场边界条件、物面边界条件和对称边界条件;模拟飞机在H=8 km,Ma=0.8飞行时的情况。由于需要考虑空气压缩性,采用无反射压力场边界条件;物面边界条件为无滑移、无穿透;由于不考虑横航向的气动参数,所以使用了对称边界条件,以减少网格数量。
2 计算结果分析
2.1 四模型纵向气动特性对比
针对无损模型、破片、离散杆和连续杆战斗部打击下的损伤模型,计算了其在H=8 km,Ma=0.8条件下,不同迎角下的升力系数、阻力系数和俯仰力矩系数。计算结果如图3所示。

图3 四模型气动特性Fig.3 Aerodynamic characteristics of the four models
由图3可知:(1)破片和离散杆战斗部造成的损伤对升力的影响,无论是在大迎角还是小迎角时均比较小;而连续杆战斗部造成的损伤在小迎角时影响较大,大迎角时影响较小。(2)三种战斗部所造成损伤对阻力的影响均比较小。(3) 连续杆战斗部造成的损伤对俯仰力矩的影响,无论是在大迎角还是在小迎角下,明显比破片和离散杆大,可能的原因是该飞机的焦点在翼尖附近。
从量值上看,三种损伤形式对升力、阻力影响均不明显,破片、离散杆造成的损伤对俯仰力矩有一定影响,但连续杆造成的损伤对俯仰力矩的影响非常大,是否会造成该飞机在巡航状态下的杀伤,还需要进一步研究。
2.2 连续杆损伤纵向配平研究
基于以上分析,连续杆造成的损伤对该飞机在巡航状态下俯仰力矩的影响非常大,可能会影响到飞行安全,因此,需要研究此时该机的纵向配平问题。
根据纵向平衡方程式(2)和式(3),计算配平所需要的迎角和舵偏角,根据是否在许用范围内研究纵向配平问题。
CL=CLα(α-α0)+CLδeδe
(2)
Cm=Cm0+Cmαα+Cmδeδe
(3)
由纵向平衡方程可知,纵向配平问题的研究首先需要进行相关气动导数的计算,计算结果如图4所示。

图4 连续杆损伤模型气动参数Fig.4 Aerodynamic parameters for continuous rod damage model
由图4(a)可知,在迎角为4°时,损伤飞机俯仰力矩随迎角的变化趋势发生了转折。由于这一特殊变化,该飞机的纵向配平问题需要按照迎角为(-2°~4°)和(4°~16°)两个区域分别进行。计算中假设该飞机此时的重量为6 500 kg,计算出式(2)中的升力系数。
对于小迎角区域(-2°~4°),通过线性拟合图4中的相关气动参数,得到计算纵向配平问题所需要的相关气动导数,如表1所示。

表1 小迎角区域气动导数Table 1 Aerodynamic derivatives for small angle of attack
由式(2)和式(3)计算可得该飞机在巡航时所需迎角为4.12°,舵偏角为-1.71°。虽然舵偏角在许用范围内,但由图4(a)可知,迎角不在拟合范围之内,也不符合变化趋势。
对于大迎角区域(4°~16°),类似前面的分析,计算得到纵向配平问题所需要的相关气动导数,如表2所示。
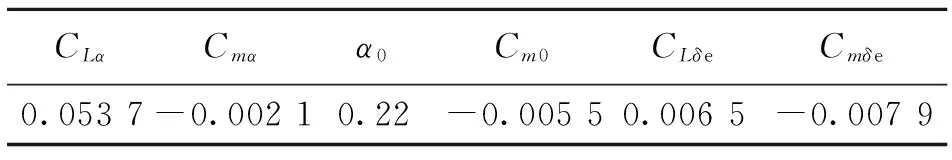
表2 大迎角区域气动导数Table 2 Aerodynamic derivatives for large angle of attack
计算可得该飞机在巡航时所需迎角为3.83°,舵偏角为-1.71°。虽然舵偏角在许用范围内,此时迎角不在拟合范围之内,也不符合其变化趋势。
综上所述,该飞机在连续杆战斗部损伤翼尖后,当重量为6 500 kg,以巡航高度和速度飞行时,纵向是不能配平的。虽然此时不能配平,但是所需迎角4.12°与图4(b)中俯仰力矩随迎角变化的转折点4°相差甚小。所以,需要分析当迎角为4°时,飞机配平后能提供的升力。
对此,首先假设迎角为4°,根据式(3)求得所需舵偏角为-1.734°;然后根据式(2)算出所能提供的升力系数为0.177 5;最后通过空气动力学基本公式计算出巡航状态下,该飞机在被打掉翼尖附近的部分机翼后,迎角为4°,舵偏角为-1.73°时,可以提供6 311.5 kg的升力。与之前的6 500 kg相比,此时的重量仅减小了188.5 kg。
该飞机的正常起飞重量为7 370 kg,正常着陆重量为5 480 kg。在作战受损后,由于燃油消耗和武器投放,其重量会有一定程度的减小。此时如果重量小于6 311.5 kg,纵向是可以配平的,反之,则不能配平。该飞机在巡航状态下,当重量为6 500 kg时,翼尖附近机翼的损失会导致其纵向不能配平。但是,只要此时的重量小于或等于6 311.5 kg,该飞机依然是可以配平的。
3 结束语
以某型作战飞机为研究对象,分别建立其在破片、离散杆和连续杆战斗部打击下的损伤模型;计算分析了该飞机在系统及机体结构基本完整的情况下,机体表面损伤对其巡航状态下纵向气动特性的影响;对于影响严重的连续杆战斗部造成的损伤,重点研究了其在巡航状态下的纵向配平问题。研究结果对于战损飞机杀伤状态的判断及飞控重组问题,具有一定的参考价值。
[1] Ball R E. The fundamentals of aircraft combat surviva-bility analysis and design [M]. 2nded. Reston: AIAA, 2003:660-695.
[2] Ball R E.飞机作战生存力分析与设计基础[M].林光宇,宋笔锋,译.北京:航空工业出版社,1998:101-127.
[3] 韩庆.飞机易损性评估方法研究[D].西安:西北工业大学,2000.
[4] 李向东,钱建平,曹兵,等.弹药概论[M].北京:国防工业出版社,2004:261-266.
[5] 刘彤.防空战斗部杀伤威力评估方法研究[D].南京:南京理工大学,2004.
[6] 纪乒乒,陈金艵.ANSYS ICEM CFD网格划分技术实例详解[M].北京:中国水利水电出版社,2012:217-221.
[7] 陈科甲,白俊强,朱军.发动机短舱对翼身组合体跨音速气动特性影响研究[J].航空计算技术,2010,40(1):64.
[8] Menter F R. Zonal two-equationk-ωturbulence model for aerodynamic flows[R].AIAA-93-2906, 1993.
Influenceofcombataircraft’swingsurfacedamagedonlongitudinalaerodynamiccharacteristics
GAO Yu-wei1, HAN Qing2, ZHANG Feng2, LIU Xing2
(1.Fuselage Design Institute, Xi’an Aircraft Design Institute, Xi’an 710089, China;2.College of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)
Vulnerability assessment of combat aircraft is one of the basic issues in the survivability design and evaluation process. This paper takes the certain type of fighting aircraft as the research target to establish the three representative damage models. The longitudinal aerodynamic characteristics of the damage models and the normal model in cruised condition is calculated based on the N-S equation numerical simulation. For the damage model of continuous rod warhead, this paper further studies the vertical balancing problems at this time. The results of the study show that, compared to fragment and discrete bar warhead, the effect of damage caused by continuous bar warhead is more significant. It may even lead to the aircraft’s ruin under the particular state. The result of this paper can be used for the judgment of fighting damaged aircraft’s kill guidelines.
combat aircraft; vulnerability; warhead; aerodynamic characteristic
V211.3; V221
A
1002-0853(2013)05-0394-04
2013-03-18;
2013-05-27; < class="emphasis_bold">网络出版时间
时间:2013-08-21 16:15
973计划项目资助
高玉伟(1981-),女,河北唐山人,工程师,主要从事飞机设计工作;韩庆(1969-),男,陕西西安人,副教授,研究方向为生存力与结构优化等。
(编辑:李怡)

