变形问题在一元函数微积分学中的体现

王志超 (中国传媒大学经济与管理学院，北京 100024)

变形问题在一元函数微积分学中的体现

王志超 (中国传媒大学经济与管理学院，北京 100024)

以一元函数微积分学中3个典型的变形问题(导数形式与极限形式的相互转变、不定积分形式与导数形式的相互转变、定积分形式与抽象函数形式的相互转变)为视角，通过对实例的分析与反思，研究了变形问题的命题依据和解题策略。

一元函数微积分；变形；数学关系；原函数；抽象函数

变形是数学学科的基本技能之一，在形形色色的数学问题中涉及广泛。由于它需要考验解题者对于数学形式特征的敏感程度，对思维的跳跃性要求较高，许多教材又很难成体系地归纳出方法的定论，所以成为了许多同学在解题中难以逾越的鸿沟。在学习中，如何突破这一“瓶颈”呢？笔者认为，一方面，要剖析命题者设计这个变形题的依据是什么，清楚往哪里变；另一方面，要深究解题者实现这个变形的关键点是什么，清楚怎么变。下面就以一元函数微积分学中3个典型的变形问题为视角，谈一谈笔者对于变形的拙见。

1 导数形式与极限形式的相互转变

1.1正向：变极限式为导数式

(2)本题是不是x0-h看作“x0”，2h看作“Δx” 呢？不是。因为题中只交代了f′(x0)存在，并未说明f′(x0-h)是否存在。故只能把x0看作“x0”，h和-h看作“Δx”。由于题中没有f(x0)项，可在分子先加f(x0)再减 ，并将分式拆成2项，即：

反思如何将极限式凑成导数的定义式？

(i)关注x0和Δx的抽象性。“x0”可以是数，也可以是实在的x0，但必须满足“f′(x0)”存在；“Δx”可以是h，可以是含变量x的代数式，也可以是实在的Δx，但必须符合“f(x0+Δx)”的形式。

(ii)关注Δx的一致性。导数定义式中“ Δx→0”中的“Δx”、“f(x0+Δx)”中的“Δx”、分母的“Δx”三位一体，形式一致是凑型的重要依据。如问题(3)， sin2x+cosx-1之所以能看作“Δx”，还因为当x→0时满足sin2x+cosx-1→0。

(iii)关注方法的针对性。例1中问题(1)的核心步骤是分子分母同时乘以-1，针对的是题中分子分母都相差一个负号，不妨称为“正负凑型”；问题(2)的核心步骤是在分子先加f(x0)再减f(x0)，针对的是题中没有f(x0)项，不妨称为“加减凑型”；问题(3)的核心步骤是在原式先除sin2x+cosx-1再乘sin2x+cosx-1，针对的是题中分母不是“Δx”，不妨称为“乘除凑型”。这是将极限式凑成导数定义式的3种典型的情境。

1.2逆向：变导数式为极限式

反思如何借助已知的极限求导？

(ii)本例中，虽然问题以导数的面孔出现，但关键步骤用到的却是极限的方法，即把求导数的问题转化为了已知极限求参数值的问题。推广至所有以“借鉴关系”为命题依据的变形问题，变形时要学会转化。因为是借鉴关系，问题往往容易产生交汇，产生交汇就难免相互转化，解决的方法自然也难免要相互借鉴。本例与通过把函数变形为方程求值域，通过把方程记作2个函数判断根的情况等问题“题出同门”，都是以借鉴关系为命题依据的变形问题。

2 不定积分形式与导数形式的相互转变

2.1正向：变导数式为不定积分式

反思如何使导数与不定积分转化自如？

(i)当同时涉及导函数和原函数时，要理清其关系，即谁是谁的导函数，谁是谁的原函数，做到不颠倒。

(ii)当同时涉及多个任意常数C时，要明确其来源，即每一个任意常数是由哪一次积分所得，并用不同的下标加以区分，做到不遗漏，不混淆。

2.2逆向：变不定积分式为导数式

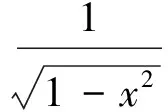
反思如何借助已知的不定积分求另一不定积分？

(ii)本例的关键在于求f(x)，求f(x)的关键在于去积分号，而只有导数才能抵消积分，故等式两边同时求导，变不定积分式为导数式是唯一的选择。推广至所有以“互逆关系”为命题依据变形问题，变形时要学会抵消。互逆运算最大的特点就是能相互抵消，就好比减法能抵消加法，除法能抵消乘法，平方能抵消根号，对数能抵消指数。因此，成为变形障碍的运算可考虑用其互逆运算来抵消。本例的等式两边同时求导与解无理方程时等式两边同时平方，求幂指函数的导数时等式两边同时取对数等方法有异曲同工之妙。

3 定积分形式与抽象函数形式的相互转变

3.1正向：变定积分式为抽象函数式

分析从结论入手，适合用分部积分法:

再从条件入手，f′(2),f(2),f(0)的值恰好已知。故原式=5-3+1=3。

反思何借助已知的函数值求抽象函数的定积分？

(ii)遵循必要的“程序化”规则很重要：本例中，将上、下限代入后得到的3个函数值f′(2),f(2),f(0)恰好已知看似是巧合，但这种巧合一定程度上基于用分部积分法求定积分的“程序化”规则：边积边代限。如若不遵循这个规则，一旦被积函数“抽象”了，算不出具体的不定积分结果，“要不要带限”，“什么时候带限”都会引起歧义。这时，这种“巧合”的出现恐怕要颇费些周折了。所谓“程序化”，就是像电脑程序一样，按部就班地规定好先做什么，再做什么。遵循必要的程序有助于从容地应对特殊情境，减少出错的机会，使解题过程变得顺畅。

3.2逆向：变抽象函数式为定积分式

4 结 语

综上所述，围绕一元函数微积分学的极限、导数、不定积分、定积分都可以涉及变形问题。笔者认为，变形问题来源于数学关系。有数学关系就有数学形式，有数学形式就可以互相转变形式。换言之，极限、导数、不定积分、定积分以及抽象函数之间存在着内在的关系(借鉴关系、互逆关系、展开关系)，当然这些关系都有各自的渊源(导数定义、互逆运算、牛顿-莱布尼茨公式)。总之，这些关系“服务”了命题者，却“害苦”了解题者。那么，如何使解题者不再痛苦呢？正所谓“知己知彼，百战不殆”，解题者应当换位思考，去研究命题者是依据什么想出这道题的。因为依据借鉴关系，所以考虑转化；因为依据互逆关系，所以考虑抵消；因为依据展开关系，所以考虑选择。这就是“往哪里变”。

[1]同济大学数学系.高等数学(上册)[M].第6版.北京:高等教育出版社,2007.

[2]武忠祥.数学考研历年真题分类解析[M].西安:西安交通大学出版社,2006.

[编辑] 洪云飞

O172.1

A

1673-1409(2013)25-0134-04

2013-06-08

王志超(1994-)，男，现主要从事传媒经济方面的学习。