预腐蚀对多部位损伤发生概率的影响
张建宇 袁 军 时新红
(北京航空航天大学 航空科学与工程学院,北京100191)
多部位损伤(MSD,Multiple Side Damage)是指在同一个结构中的相似细节在循环载荷作用下产生一群长度相近、互相影响的宏观相对小裂纹,或是一条长裂纹向一群这样的裂纹扩展.这些裂纹的存在会显著降低结构的剩余强度,甚至会造成灾难性的后果[1].2010年11月,美国联邦航空局颁布了最新的适航规章[2],明确指出无论新设计的飞机还是在役飞机,都应给出一个限制期,应通过分析和试验表明结构在这个期限内不会发生MSD.
飞机结构中存在大量的成排铆钉孔结构,其使用及停放过程中的预腐蚀问题是不可避免的.关于疲劳载荷下的MSD发生问题,文献[3]提出了一种新的MSD发生概率计算方法,可以通过单一细节疲劳寿命的分布特征,估算出多细节结构的MSD发生概率;但是预腐蚀影响下的MSD发生概率研究还未见相关文献资料.因此研究这些相似细节结构在预腐蚀后发生多部位损伤的概率具有重要的意义.
本文提出了一种新的预腐蚀后多细节结构MSD发生概率公式,在单细节试验的基础上得到预腐蚀影响系数.将不经过预腐蚀处理进行的疲劳试验规定为常规试验,通过常规试验结果,结合预腐蚀影响系数,预测预腐蚀后任意细节数、任意寿命下的MSD发生概率,以及任意细节数、任意可靠度下MSD发生时的寿命,进而分析预腐蚀对MSD发生概率的影响.
1 预腐蚀后MSD发生概率公式推导
在对预腐蚀处理后的多细节结构MSD发生概率进行计算时,根据文献[4-5]中的结论,做出两个假设:①假设在预腐蚀处理后,单细节结构寿命仍然符合对数正态分布.②假设单细节结构对数疲劳寿命的分散性只与应力水平有关,预腐蚀条件对疲劳寿命的分散性没有影响.那么,在计算MSD发生概率PMSD时,无论是否有预腐蚀的影响,对数疲劳寿命标准差均取常规条件下相同应力水平时裂纹萌生寿命的对数寿命标准差.
预腐蚀影响系数C定义[6]为
其中,NC50表示预腐蚀后,对应应力水平下的单细节疲劳试验的中值寿命;N50表示常规单细节疲劳试验的中值寿命.
根据中值寿命与对数寿命均值的关系,预腐蚀影响系数C可以通过对数寿命均值表示为

其中,μC表示预腐蚀后的单细节疲劳试验的对数寿命均值;μ表示单细节常规疲劳试验对数寿命均值.
预腐蚀后的单细节疲劳寿命N服从对数正态分布,则对数寿命lgN服从正态分布,即lg N~N(μC,σC).预腐蚀后单细节对数寿命的概率密度函数fC(x)就可以用正态分布的形式表示为

由式(2)可推出,预腐蚀后对数寿命均值为

根据假设②,fC(x)可以用常规试验单细节对数寿命均值μ、标准差σ及C表示:
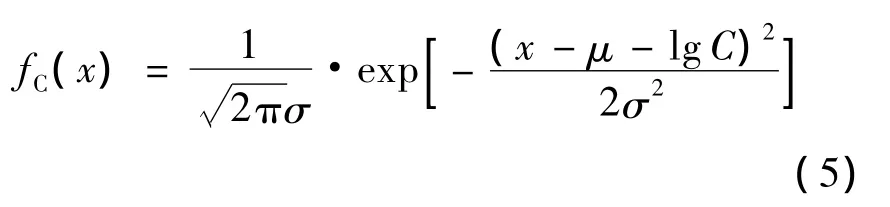
假设飞机相似多细节结构各细节相互独立,相互之间不会发生影响.飞机相似多细节结构各细节之间应力差异很小,所处的工作环境相同,可以认为这些细节承受相同大小的应力水平,并且预腐蚀条件相同.从初始到循环数N时,各个细节裂纹萌生概率为


结合文献[3]中常规试验MSD发生概率公式,提出预腐蚀后的PMSD计算公式为其中,N为对应的疲劳寿命;n为细节数.通过上述公式可以看出,只要得到了C,就可以通过单细节常规试验的结果,预测预腐蚀后任意细节数孔板寿命为N时的MSD发生概率,或任意细节数孔板某可靠度下发生MSD时的疲劳寿命.

2 预腐蚀影响系数C的测定
通过对7B04-T74δ2.0铝合金板材进行单细节的常规疲劳试验与预腐蚀后的疲劳试验,得到预腐蚀影响系数C.试验机为INSTRON-8803电液伺服材料试验机.常规疲劳试验采用载荷控制的方法,疲劳载荷为等幅谱,波形为正弦波,加载频率为 15 Hz,应力比 R=0.1,应力水平 S=87.5 MPa.
单细节试件是指只含有一个危险部位,当此部位产生疲劳裂纹或者断裂时,认为该试件发生破坏.但是为了节省资金及试验的时间可以采用串联双细节试件进行单细节试验.
所谓串联双细节试件是指在同一个试件中,串联布置两个细节,两孔间的距离足够远,使得加载时两个细节受载荷情况完全独立,在其中一个孔断裂后,可对另一孔继续加载至断裂,从而得到两个有效数据,节省了试验时间和试验成本.图1为串联双细节试件形式及加载方向.

图1 串联双细节孔板(单位:mm)
预腐蚀的方法为3.5%NaCl溶液连续浸泡240 h.预腐蚀按照《JB7901—1999金属材料实验室均匀腐蚀全浸试验方法》进行.预腐蚀后的疲劳试验同样为载荷控制,等幅谱加载,波形为正弦波,应力比R=0.1,加载频率为15 Hz,应力水平S=87.5 MPa.
单细节常规疲劳试验对数寿命均值与对数寿命标准差如表1所示.
预腐蚀处理后进行疲劳试验,得到预腐蚀后对数寿命均值,结果如表2所示.
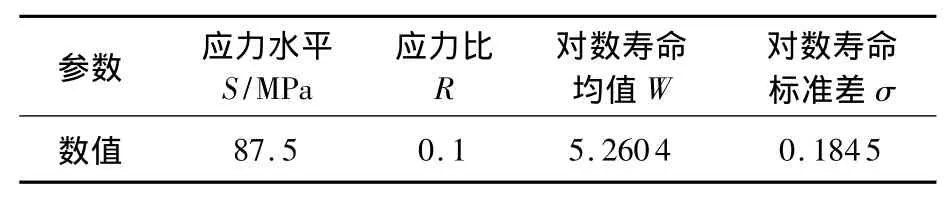
表1 单细节常规试验结果

表2 预腐蚀后单细节疲劳试验结果
通过上述单细节常规疲劳试验及单细节预腐蚀后疲劳试验结果,利用式(2)可得到经过3.5%NaCl浸泡240 h后,应力水平S=87.5 MPa所对应的预腐蚀影响系数:

3 MSD发生概率计算
3.1 多细节试验
多细节试验同样采用7B04-T74δ2.0铝合金板材,分别进行三细节孔板常规环境疲劳试验及五细节孔板预腐蚀-疲劳试验.试验中所用的试验机及加载方式均与单细节试验相同,应力水平仍取S=87.5 MPa.三细节、五细节试验件尺寸分别见图2、图3.三细节孔板不做预腐蚀处理,直接进行疲劳试验,共9件.五细节孔板先用3.5%NaCl溶液浸泡240 h,再进行疲劳试验,共3件.

图2 三细节孔板试件(单位:mm)
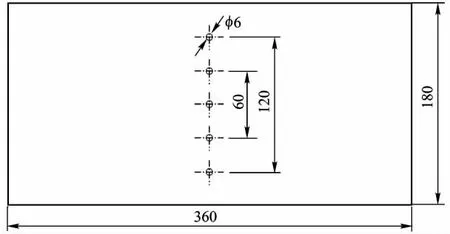
图3 五细节孔板试件(单位:mm)
在疲劳试验过程中,分别记录每一试件、每一孔的裂纹萌生寿命,得到第二条裂纹萌生时的疲劳寿命,即为多细节结构发生MSD时对应的疲劳寿命NMSD.
各个试件的存活率[4]为

破坏率(即MSD发生概率)为

其中,i表示各试件按出现多裂纹时对数寿命由小到大排列的顺序号;n表示该组试验的有效数据个数.
三细节常规疲劳试验结果如表3所示,五细节预腐蚀后疲劳试验结果如表4所示.
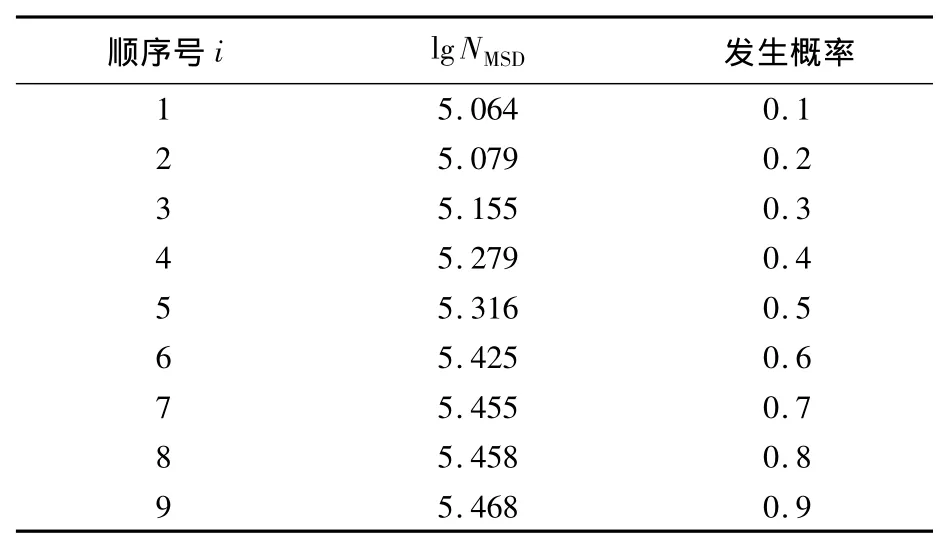
表3 三细节常规试验结果

表4 预腐蚀后五细节试验结果
3.2 MSD发生概率
利用单细节常规疲劳试验结果μ=5.260 4,σ=0.1845,预腐蚀影响系数C=0.7506,及细节数n=3,n=5,通过文献[3]中的方法及式(7)分别计算得到常规疲劳试验及预腐蚀影响后,三细节和五细节孔板的PMSD-lgN曲线.
三细节孔板预腐蚀及常规条件下的PMSD计算所得PMSD曲线及三细节孔板常规环境下疲劳试验结果如图4所示.

图4 三细节孔板计算及试验结果
从图4可以看出,三细节孔板常规环境PMSD预测结果与试验结果相比,预测趋势与试验结果一致.另外预腐蚀对MSD发生概率有促进作用,预腐蚀后相同寿命对应的PMSD明显增大.这也证实了所建立的多部位损伤发生概率估算方法的合理性与可行性.
五细节孔板预腐蚀及常规条件下的PMSD计算所得PMSD曲线及五细节孔板预腐蚀后疲劳试验结果如图5所示.

图5 五细节孔板计算及试验结果
由图5可以看出,五细节孔板预腐蚀后PMSD预测结果与试验结果相比,预腐蚀后同寿命对应的PMSD值同样明显增大.另外在PMSD较小时,公式计算结果略偏于危险;在PMSD较大时,公式计算结果略偏于保守,并且计算结果与预腐蚀后疲劳试验结果一致.
4 预腐蚀对MSD发生概率的影响
结合预腐蚀处理后多细节孔板疲劳试验结果,采用固定相关变量,例如循环数N、相似细节数n、可靠度R'的方法,比较预腐蚀前后MSD发生概率或MSD发生时疲劳寿命的计算所得值,分析研究预腐蚀的影响.
4.1 预腐蚀后细节数n对PMSD的影响
由式(6)可知,式(7)中单一细节裂纹萌生概率pC(N)与细节数n无关,只与试验中的加载方式、预腐蚀方法以及对应的疲劳寿命相关.因此在应力水平、预腐蚀条件确定的条件下,多细节孔板中任意一个细节达到寿命数N时萌生裂纹的概率pC(N)均为定值.因此可以把pC(N)看作常数,将PMSD对细节数n求导,可以得到

则在n>1且0< pC(N)<1时,PMSD对细节数n的导数大于0,即当p(N)确定的情形下,多部位损伤发生概率PMSD是关于细节数n的增函数.因此,在相同的试验条件、相同的疲劳寿命时,PMSD随细节数n的增大而增大.

图6 N=105时PMSD随n的变化趋势
在应力水平取87.5 MPa时,给定载荷循环数N=105,取细节数 n=3,5,7,9,…,计算 N=105时不同细节孔板的MSD发生概率,分别得到预腐蚀前后MSD发生概率随细节数n的变化趋势,如图6所示.由图6可看出,N=105且细节数较小时,相同细节数下,预腐蚀影响下的MSD发生概率明显偏大,预腐蚀后的PMSD-n曲线斜率较大,PMSD增大较快.在细节数n较大的阶段,预腐蚀与常规试验的PMSD均趋近于1,MSD必然发生.
4.2 n对预腐蚀后MSD发生时对数寿命的影响
给定应力水平 S=87.5 MPa,可靠度R'=0.95,计算发生MSD时对数寿命lgNMSD随细节数n的变化,如图7所示.
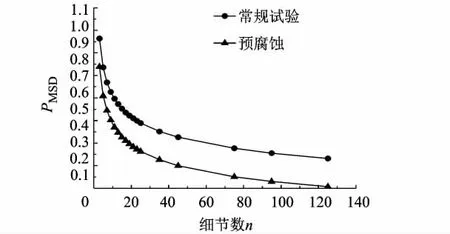
图7 R'=0.95时lgNMSD随n的变化趋势
由图7可看出,对某一给定的可靠度,无论是否经过预腐蚀处理,发生 MSD时的对数寿命lgNMSD均随细节数n的增大而减小,且当细节数较大时,变化趋于平缓,并接近于一条平行于x轴的渐近线.
5 结论
利用预腐蚀后疲劳试验测得的预腐蚀影响系数,计算了预腐蚀后的含相似多细节结构中MSD发生概率,同时讨论了预腐蚀对MSD发生概率的影响,可得到如下结论:
1)采用预腐蚀后PMSD公式计算得到的预腐蚀后的PMSD-lgN曲线,计算所得曲线可以较好地反映实际情况.预腐蚀与常规试验的PMSD曲线,当PMSD较小时,计算结果均略偏于危险,PMSD较大时,计算结果均略偏于保守.
2)随细节数的增加,相同寿命时,预腐蚀与常规试验的PMSD均不断增大,预腐蚀后的PMSD曲线斜率更大.
3)预腐蚀与常规试验相同可靠度下的NMSD均随细节增大而不断减小,预腐蚀与常规试验的lgNMSD-n曲线变化趋势相同.预腐蚀后相同细节数的lgNMSD变小,预腐蚀明显加速MSD的发生.
References)
[1] Draft FAA Advisory Circular No 120-YY Widespread fatigue damage on metallic structure as originally released in 2006 for public comment[S]
[2] Federal Aviation Administration.Ageing airplane program:widespread fatigue damage,final rule[R].FAA,14CFR Part 25,26,121,2010
[3] Zhang Jianyu,Bao Rui,Zhang Xiang,et al.A probabilistic estimation method of multiple site damage occurrences for aircraft structures[J].Procedia Engineering,2010,2(1):1115-1124
[4]高镇同.疲劳应用统计学[M].北京:国防工业出版社,1986 Gao Zhentong.Fatigue applied statistics[M].Beijing:National Defense Industry Press,1986(in Chinese)
[5]贺小帆,刘文珽,王忠波,等.疲劳寿命预腐蚀影响系数曲线通用性研究[J].机械强度,2004,26(1):110-104 He Xiaofan,Liu Wenting,Wang Zhongbo,et al.Research on the generality of the pre-corrosion influence coefficient curve of fatigue life[J].Journal of Mechanical Strength,2004,26(1):110-104(in Chinese)
[6]赵学峰,王富永,赵海军.预腐蚀疲劳寿命影响系数及S-N曲线研究[J].机械强度,2008,30(6):977-981 Zhao Xuefeng,Wang Fuyong,Zhao Haijun.Research on the influence coefficient and S-N curve for the pre-corrosion fatigue life[J].Journal of Mechanical Strength,2008,30(6):977-981(in Chinese)

