超声波流量测量中流速计算方法的对比
于 洋 宗光华
(北京航空航天大学 机器人研究所,北京100191)
丁凤林
(北京控制工程研究所,北京100190)
超声波流量计因其非接触和高精度的特点,成为目前应用最广泛的流量计量仪器之一.美国2005年的数据表明,超声波流量计的年销售额已超过30亿美元,占所有类型流量计总销售额的10%以上[1].近年来随着电子技术的飞速发展,超声波流量计的测量精度得到了很大提高,目前已经应用到了化工、水利、石油、天然气、医疗等各个领域.超声波流量计的原理是超声波在流体中传播时,其传播速度会受流体流速影响而变化,因此可以通过测量穿过流体的超声波信号来计算流体的流速.据此,所采用的测量方法主要有传播时间差法、频率差法、相关法、多普勒效应法等[2-5].其中传播时间差法和频率差法只需要获知超声波的传播时间(或频率),电路实现和测量计算相对容易,故在超声波流量计中使用较为广泛.本文在研制超声波流量计的基础上,针对传播时间差和频率差这2种实现方法,做了详细的对比研究,并通过实验分析对比了2种方法的实际效果.
1 超声波流量测量方法
1.1 时间差法
超声波流量计的声道布置有多种形式,如V法、Z法、W法等[6].这里为了简化问题,使用换能器对射的传统布置形式,如图1所示.换能器A和换能器B分别安装在管路的两侧,且从一侧换能器发射出的超声波经过楔块和管路传播后恰好进入另一侧换能器.管路中流体的流动方向为从左至右,流速大小为u,超声波在流体中的传播距离为L(图1中d点和e点间的直线距离),传播路径(图1中虚线d→e)与管路的夹角为θ,超声波在水中的声速为c.

图1 超声波流量计原理图
严格地说,超声波从一侧换能器发出,到另一侧换能器接收到,传播总时间tt由3部分组成:

其中,td是电路的延迟时间,为常量;tw是超声波在管壁中的传播时间,也为常量;tf为超声波在流体中的传播时间,随流体速度而变化.这3项中,仅第3项tf对计算流体速度有贡献.超声波顺流(downstream)和逆流(upstream)的传播时间为

需要说明的是,这里计算得到的tu和td均为上面提到的tf.由此可计算得测量流速的超声波传播时间差法:

1.2 频率差法
与时间差法对应的是频率差法,顺流和逆流的超声波传播频率分别定义为

同样可求得测量流速的超声波传播频率差法:

2 2种方法对比分析
至此得到了超声波测量流速的2种方法,即时间差法和频率差法.这2种方法在现场应用环境下会受到下列因素影响而呈现不同的行为.
1)环境温度的变化.因为声速c通常随温度变化,所以当环境温度波动较大时,时间差法(式(4))的计算精度就要受到影响,而频率差法(式(7))中因为没有引入声速c,故不受温度影响.
2)时间测量的准确性.在实际中测量到的是超声波从一个换能器到另一个换能器的总传播时间tt,其中包含td,tw,tf3项.对照上述2种方法,在计算流量时,需要的仅是超声在流体中的传播时间tf(包括tu和td).超声波在流量计中的传播时间微乎其微,通常只有100 μs的量级,因此信号的延迟影响是不能忽视的.在时间差法流量计算中,td和tw这2项常量在计算时间差(tu-td)中抵消了,因此不受这一因素影响.而频差法的计算式(5)和式(6)中的顺逆流时间如果用超声波传播总时间tt代替tf计算,必然给结果带来误差.
3)不确定度的计算.由式(4)和式(7),分别计算时间差法和频率差法的流量,以计算不确定度[7],得到

其中Δt=tu-td.从上面的分析可知,事实上电路测到的是超声从一侧换能器到另一侧换能器的总传播时间tt,却无法准确获得 tu和 td,不过应指出,顺流和逆流的时间差Δt是准确的,不受电路延迟和管壁厚度的影响.另一方面,声速c虽然随着环境温度的波动而变化,但Δt的数量级很小,故温度变化带来的声速不确定度较小.从这2方面考虑,就不确定度而言,时间差法的计算结果较频差法的结果准确.
综合以上3方面的影响,时间差法仅在环境温度的变化这一影响上不如频率差法,考虑到在不确定度的计算中指出环境温度变化引入的不确定度,相对于时间测量的不确定度,其影响微乎其微.故从理论分析的角度来看,时间差法的测量精度高于频率差法.
3 实验验证
3.1 流量计
实验中使用小管径超声波流量计[8]进行流速测量,流量计结构如图2所示,其中流量计管座结构如图3所示.上游和下游管段的内径为6 mm,中间测量管段的内径为8 mm,所有管壁的厚度均为1 mm,管座内壁厚度为1 mm,超声波在中间测量管段的有效传播长度为200 mm.

图2 超声波流量计结构

图3 超声波流量计管座结构
3.2 实验环境
为了准确地测量流量的真实值,本仪表在中国计量科学研究院液体流量室进行了时间差法和频率差法的对比测量.依据JJG 1030—2007《超声波流量计检定规程》,测量现场见图4,测试平台由超声波流量计、接收和处理电路、微型计算机和水流量基准装置组成.流量标准装置组成见图5.

图4 流量测量现场

图5 流量标准装置
流量测量在温度25℃、湿度59%RH的环境下进行,实验介质为清水,介质温度25.2℃,流量测量范围为0~150 mL/s.按照流量计检定标准,测量点设为 5 个,分别为 15,40,80,120,150 mL/s,每个测量点测试次数为3次.超声波流量计采样频率10 Hz,每点每次测量30 s.本实验的目的是比较超声传播时间差法和频率差法计算流量的准确性,因此结果中使用的时间差法测得的流量、频率差法测得的流量均为未使用流量计校准系数的原始数据,即由流量计测得顺流、逆流的传播时间后,根据式(4)和式(7)计算得到的流量数据.
3.3 对比分析
流量计的测量结果如图6所示,其中标准值由流量标准装置给出.

从图6可以看出,时间差法测得的流量数据和标准值十分接近,而且流量越大,时间差法的测量结果和标准值的接近程度越高.这一结果一方面和流量增大,超声波传播时间差增大,时间测量误差减小有关,另一方面和流量增大带来的流量充分发展,测量线速度越来越接近流体的平均流速有关.然而频率差法测得的流量数据和标准值的差距很大,误差高达30%,不能满足流量的测量要求.表1给出时间差法和频率差法测量结果的误差对比.

图6 时间差法和频率差法测量数据对比

表1 未校准的测量误差比较
以流量标准值为152.5 mL/s的情况为例,此时超声波顺流方向传播总时间td_t=166.166 μs,逆流方向传播总时间tu_t=166.693 μs,由此可计算出超声波传播时间差Δt=0.527 μs.
在不考虑电路互易性的前提下,设静水的情况下超声波在水中的有效传播时间(即式(1)提到的tf)为ts,则有流量的情况下的顺流、逆流的水中有效传播时间分别为

将式(10)、式(11)代入式(7),同时将流量标准值ustd代入得u2,考虑到使用的流量计声道与管路轴线夹角θ=0,可得

式(12)中只有一个未知量ts,求出ts后将其代入式(10)、式(11),可以求出顺流、逆流情况下超声波在水中的有效传播时间为

代入数据后,可求出顺流方向超声波在水中的有效传播时间td_f=131.501 μs,逆流方向超声波在水中的有效传播时间tu_f=132.028 μs.
而超声波在管壁中的传播时间tw可根据管座内壁厚度计算出,为0.329 μs.对比流量计的顺流方向、逆流方向总时间测量值td_t和tu_t,可知超声波处理电路的延迟时间td=34.665 μs.电路延迟较大,是因为在超声波发射接收电路中,使用了模拟开关来切换两侧超声波探头的发射/接收状态,同时发射电路中串联的电容也增加了电路的延迟.由此可见,电路延迟和管壁厚度对频率差法的测量精度影响很大,在计算中不能忽略.这也进一步解释了表1中的数据当流量大于78 mL/s后,时差法误差明显减小,而频差法误差无减小趋势的原因.这是由于时间差计算方法中的电路延迟时间td和管壁中超声传播时间tw在计算中相互抵消了,并且超声波传播时间随流量增加而增大,因此采用时间差计算方法的流量计误差随着流量的增加而减小.而对于频率差法来说,电路延迟时间tdelay和管壁中超声传播时间twall不能线性地互相抵消,因此采用频率差计算方法的流量计误差没有随着流量的增加而减小.
流量计校准后,再次进行实验.这里使用的是分段校准法,即分别标定在各流量段的校准系数,并且针对时间差法和频率差法采用各自的校准系数,如图7所示.以时间差法的校准系数为例,可见其在低流量的情况下,校准系数并非线性的,只有在流量大于80 mL/s后,曲线才出现线性化趋势,因此采用分段校准法是比较合理的.表2为校准后的测量误差,可以看出校准后时间差法和频率差法的测量误差均低于1‰,时间差法误差略低于频率差法.但考虑到图7中,时间差法的校准系数曲线过渡平滑,在大流量情况下几乎成线性关系,因此时间差法在0~150 mL/s所有流量范围上的测量精度将高于频率差法.需要说明的是表2中的数据仅是为了比较2种计算方法校准后的测量误差,如需鉴定流量计的精度,还需要测试更多的流量点.
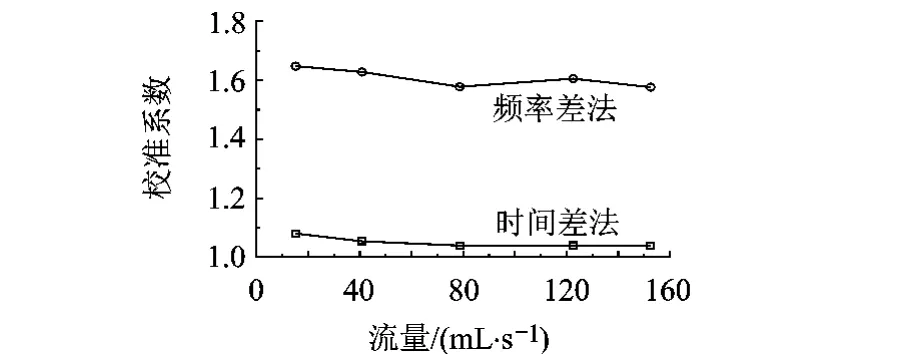
图7 校准系数曲线

表2 校准后的测量误差比较
4 结束语
本文对超声波流量测量中的2种流速计算方法,即时间差法和频率差法进行了对比和分析.从环境温度的变化、时间测量的准确性、不确定度的计算3个方面对比了时间差法和频差法在测量准确性上的差异.理论分析表明时间差法在测量精度上较频率差法有优势,具体体现在时间差法不受电路延迟和管壁厚度的影响,而这2个因素对超声波流量计的精度影响最大.
时间差法和频率差法的对比实验表明,时间差法的测量结果最接近流量真实值,而频率差法的测量结果偏差过大.这也进一步印证了理论分析中指出的电路延迟和管壁厚度对测量精度的影响.流量计校准后的对比结果表明,时间差法的校准曲线比频率差法的线性度好,曲线过渡自然,在全流量范围内能取得更高的测量精度.
References)
[1] Lynnworth L C,Liu Y.Ultrasonic flowmeters:half-century progress report,1955—2005[J].Ultrasonics,2006,44(Supplement):e1371-e1378
[2] Mandard E,Kouame D,Battault R,et al.Methodology for developing a high-precision ultrasound flow meter and fluid velocity profile reconstruction[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2008,55(1):161-171
[3] Lysak P D,Jenkins D M,Capone D E,et al.Analytical model of an ultrasonic cross-correlation flow meter,part 1:stochastic modeling of turbulence[J].Flow Measurement and Instrumentation,2008,19(1):1-7
[4] Lysak P D,Jenkins D M,Capone D E,,et al.Analytical model of an ultrasonic cross-correlation flow meter,part 2:application[J].Flow Measurement and Instrumentation,2008,19(1):41-46
[5] Calzolai M,Capineri L,Fort A,et al.A 3-D PW ultrasonic Doppler flowmeter:theory and experimental characterization[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1999,46(1):108-113
[6]贺胜,彭黎辉,仲里敏.基于CFD的超声波流量计最优声道位置研究[J].仪器仪表学报,2009,30(4):854-856 He Sheng,Peng Lihui,Zhong Limin.Computational fluid dynamics based sound path optimization for ultrasonic flow meter[J].Chinese Journal of Scientific Instrument,2009,30(4):854-856(in Chinese)
[7] Yang B,Cao L,Luo Y.High-speed and precise measurement for ultrasonic liquid flow metering based on a single FPGA[C]//Poceedings of the 2009 IEEE Intrumentation and Measurement Technology Conference.Singapore:IEEE,2009:309-312
[8] Yu Y,Zong G H.Design and simulation of an ultrasonic flow meter for thin pipe[C]//Poceedings of the 2011 IEEE/ASME International Conference on Mechatronics and Automation.Beijing:IEEE,2011:1115-1119

