基于相关分析和组合神经网络的退化预测
党香俊 姜同敏
(北京航空航天大学 可靠性与系统工程学院,北京100191)
对性能退化的有效预测是加速退化试验和故障预测与健康管理领域的关键技术.在故障预测与健康管理中,对系统关键部件剩余寿命的准确预测能够有效预防系统事故的发生,使工程人员根据系统运行情况合理规划和实施维修计划,从而避免过度维修,降低寿命期内的维修成本.而对于加速退化试验,退化轨迹的长距离有效预测,意味着退化试验不需要进行到产品故障或接近于故障,使得试验时间显著减少,试验成本大幅降低.尤其是对于产品本身昂贵并且研究进度紧张的情况,这一作用更加明显.
为了满足工程实际的需要,越来越多的研究人员开始关注这一领域,并且应用不同理论提出了一些预测模型.从现有的文献来看,预测模型主要可以分为基于物理的模型、基于知识的模型和数据驱动的模型三大类.基于物理的方法通常使用由直接或间接影响相关组件健康状态的物理过程抽象出的数学模型,模型的建立需要丰富的专业知识,并且模型的参数验证需要大量实际数据,成本过高[1-3].基于知识的方法利用产品所属领域内的各种历史信息进行预测,虽然不再需要物理模型作为假设,但对信息量的要求过高[4].数据驱动的方法基于统计和学习技术,可以分为基于统计的方法和基于人工智能的方法.基于统计的方法以统计理论为基础,主要应用贝叶斯理论和随机过程理论及其演变形式进行建模[5-7].基于人工智能的预测方法,以采集到的性能数据作为输入,应用神经网络模型及其演变形式进行预测.神经网络不需要预先做出输入条件假设和统计模型,显著简化了模型的建立过程.此外,神经网络模型对输入数据的要求低,对于其他方法难以处理的非线性、高阶、时变动态和一些不具有分析模型的复杂过程,也都具有很好的处理能力.文献[8]根据故障发展的多变量趋势,应用自组织神经网络预测了轴承系统的剩余寿命.文献[9]以最小量化误差为指标,采用自组织映射图和BP(Back Propagation)神经网络对滚珠轴承的剩余寿命进行了预测.文献[10]基于传感器信号,使用动态小波神经网络计算并连续更新组件的剩余寿命分布.
在实际预测中,性能退化预测方法主要还需要在以下两个方面做出改进:①复杂数据预测的准确性有待提高.对复杂的退化数据,预测结果有时会与真实值存在较大差距.②预测的距离需要提升.预测的有效距离是影响退化预测作用范围的重要因素,较长距离的寿命预测能够为预防性维修决策提供更大的便利.
为了解决上述问题,本文提出了一种以相关分析和组合神经网络为基础的退化预测方法.首先,根据退化数据的特点,选择合适的参数对原始数据进行小波变换,降低退化数据的复杂性.其次,对变换后的序列,采用Durbin-Watson检验和偏相关图进行相关分析,检验小波变换参数选择的合理性.最后,根据小波变换后序列的特点,组合BP和小波神经网络进行退化预测.为了验证方法的适用性,本文对某电子产品的实际退化数据进行了预测,最后给出与单独采用小波神经网络方法的对比分析.
1 小波变换与相关分析
为了获得较好的预测结果,本文采用小波变换将复杂数据分解成一系列简单的子序列,而子序列所具有的规律性是影响预测效果的关键因素.因此,对分解后的子序列进行自相关分析是必不可少的.
1.1 离散小波变换
设采集到的信号 Hjf为能量有限信号 f∈L2(R)在分辨率2j下的近似,则Hjf可以进一步分解为f在分辨率2j-1下的近似Hj-1f,以及位于分辨率2j-1相应的细节Dj-1f之和.
设φ与ψ分别为尺度函数和小波函数,则信号f在分辨率2j-1下近似Hj-1F和细节Dj-1f分别假设为
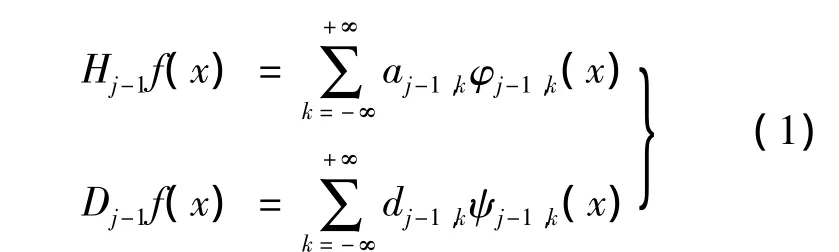
其中aj-1k与dj-1k分别为分辨率2j-1下粗糙系数与细节系数,而分辨率2j下信号f的近似Hjf可以直接写成

以此类推,信号Hjf可继续进行多级分解,如图1所示.

图1 信号分解
将式(1)代入式(2),结合图1所示的多级分解结构,可得到如下多级分解算法:

信号重构是分解的逆算法,重构过程如图2所示.

图2 信号重构
1.2 自相关分析
1.2.1 Durbin-Watson检验
影响时间序列预测效果的主要因素是未来数据对已有数据的依赖性,即序列的前期数据包含后期数据特征信息的多少.若序列具有较高的自相关性,则应用预测模型进行预测时将获得更好的预测效果.Durbin-Watson检验是一种常用的自相关分析方法,其计算简单,结果直观.对时间序列{x(t)},Durbin-Watson统计量由下式计算:

其中T为时序长度.如果时间序列{x(t)}不存在自相关性,D应趋近于2.若D为0,表明存在完全的正自相关;若D为4,则表明存在完全负相关.{x(t)}的正或负相关程度,可以由D与0或4的接近程度来判断.
1.2.2 偏相关图
由下式定义偏自相关函数φkk,当然也是作为过程自相关函数ρk的函数.

由上式定义的φkk称为过程{x(t)}滞后k的偏相关,是x(t)和x(t-k)在扣除了中间变量x(t-1),x(t-2),…,x(t-k+1)的影响滞后的偏相关.
2 组合神经网络
2.1 BP神经网络
BP神经网络是一种采用BP算法的多层感知器神经网络模型,它由输入层、中间层和输出层组成.中间层也就是隐含层,可以是一层或多层.图3是一个具有三层网络结构的简单BP神经网络模型,其中间层为一层.

图3 三层BP神经网络
其中,(x1,x2,…,xn)为 n 维输入向量;(y1,y2,…,ym)为m维输出向量;wj,k为输入层节点k与隐含层节点j之间的连接权值;M为隐含节点神经元个数;vij为隐含层节点j与输出层节点i之间的连接权值.
BP神经网络各隐层节点的激活函数使用Sigmoid函数(S函数).单极S函数可表示为
多输入单输出BP神经网络输入输出关系为

其中,θj为隐含层节点j的阈值;θ为输出层节点的阈值.
2.2 小波神经网络
小波神经网络[11]融合了小波变换与神经网络,将常规神经网络隐含层节点函数由小波基函数代替,相应的输入层到隐含层的权值及阈值分别由小波函数的尺度与平移参数代替,同时具备了小波变换的局部化能力和神经网络的自适应学习功能.小波神经网络输入与输出函数关系为
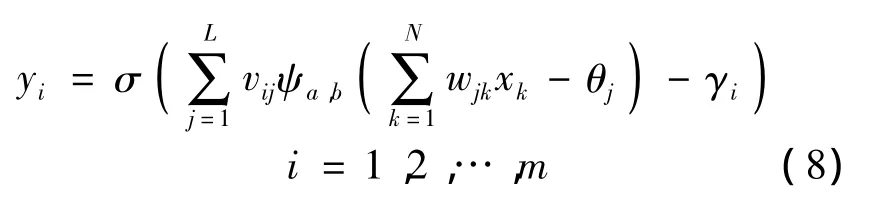
其中,xk为输入层的第k个神经元的输入;N为输入层节点神经元个数;γi为输出层i节点的阈值;L为隐含层节点数;m为输出层节点数.
产品退化预测主要以实际使用或试验中监测获得的退化数据预测监测时间点之后的性能指标.由于输入输出均为退化量值,预测过程中网络不存在输出延迟,故小波神经网络隐含层和输出层节点的阈值项可以省略,θj=0,γi=0.式(8)可以相应简化为

2.3 组合神经网络
根据离散小波分解后多级序列所具有的变化特点,选择BP神经网络和小波神经网络对不同子序列分别进行预测.式(3)中右边第一项用BP神经网络处理,第二项用小波神经网络预测.具体地,用式(7)和式(9)分别替换式(3)中对应项,同时去除各层节点的阈值,可得组合神经网络的预测公式:
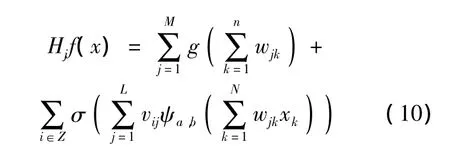
3 退化预测应用验证
上文对BP和小波组合神经网络用于产品性能退化数据预测的理论模型进行了推导,而模型在工程中的适用性尚未得到验证.为此,下面将利用某电子产品在工作应力下的退化监测数据进行退化预测的验证研究.
对该产品进行的退化试验期间共采集到了500×102min的退化数据,以其中前300×102min退化数据作为预测模型的原始数据,如图4所示.
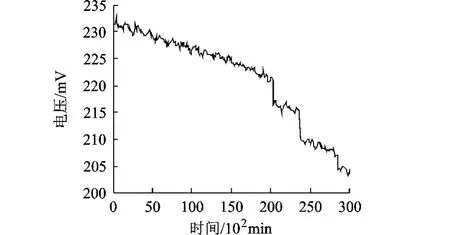
图4 原始退化数据
从图4可以看出,原始数据的退化趋势变化不规律,在 200×102,240×102和290×102min附近发生了明显的突变,并且变化幅度较大.若直接对原始数据进行预测,则对预测模型要求过高,传统预测方法很难直接给出满意的结果.为了降低退化轨迹的复杂性,本文对原始数据首先进行离散小波变换,其变换后的细节序列如图5所示.

图5 细节序列
与原始数据相比,离散小波变换后的细节序列具有较低的复杂程度,并且表现出一定的规律性.序列中前期数据包含后期数据信息量的大小,将会直接影响后续的预测效果.根据式(4),计算子序列的Durbin-Watson统计量,结果见表1.
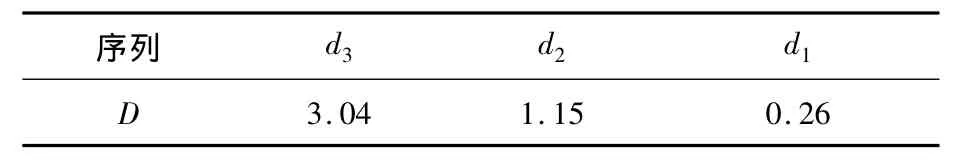
表1 Durbin-Watson统计量
由表1中可见,d3序列的D值大于2,其序列一阶相关性为负,但由于D值与4之差在0~2之间,并不能以此判断序列是否具有相关性.d2序列的D值小于2,其序列一阶相关性为正,但由于D值位于0与2之间,不能确定序列是否具有相关性.d1序列的D值接近于0,故序列具有一阶正相关性.Durbin-Watson检验没能对子序列d3和d2的自相关程度作出明确的判定,下面应用偏相关图对序列作进一步分析,给出自相关性的直观判断,如图6~图8所示.

图6 d3偏相关图

图7 d2偏相关图

图8 d1偏相关图
从图6中可以看出,d3序列具有一、二阶负相关性,也验证了Durbin-Watson检验所判定的一阶相关性为负的结论.图7表明,虽然d2的一阶偏相关系数为负,与表1判断的相关性可能为正矛盾,但由于其偏相关系数较小,故d2不具有相关性.上文应用Durbin-Watson检验法判定了d1序列具有一阶正相关性,这一结论在图8中得到直观的验证.另外,除了一阶相关性,d1还具有较强的二阶负相关性.
离散小波变换在降低原始数据复杂性的同时,也使得子序列具有较好的自相关性,减小了后续序列预测的困难.下面采用BP网络与小波神经网络相结合的方法,应用前文推导的组合神经网络式(10),对产品300×102min之后的退化轨迹进行预测.根据实际退化数据的特点,设定式(10)中相应的模型参数,得

其中网络隐层节点函数g(·)选用式(6)所示的S函数,隐层节点函数 ψa,b选择 Morlet小波.
为了缩短网络学习时间,提高收敛速度,本文采用L-M(Levenberg-Marquardt)法作为网络的学习训练算法.L-M法是一种结合了高斯-牛顿法和梯度下降法优点的快速算法,其基本思想是使其每次迭代不再沿单一的负梯度方向,而是允许误差沿着恶化的方向进行搜索,同时通过在最速梯度下降法和高斯-牛顿法之间自适应调整来优化网络权值,使网络能够有效收敛,提高了网络的收敛速度和泛化能力.
对于预测效果的验证,采用结合小波去噪的小波神经网络方法与本文提出的组合神经网络方法进行对比分析.将两种方法的预测结果分别与实际数据进行比较,如图9和图10所示.

图9 小波神经网络预测结果

图10 组合神经网络预测结果
为了评价预测轨迹与实际退化轨迹的符合程度,引入均方误差(MSE,Mean Square Error)作为评价指标:

其中At和Pt为退化数据的实际值和预测值.
根据产品失效的历史信息,选择产品的失效阈值为0.16V,则产品从第301×102min开始,到退化轨迹首次穿越0.16 V所经历的时间即为产品的剩余寿命.剩余寿命(RUL,Remaining Useful Life)预测值与真实值计算结果如表2所示.

表2 均方误差及剩余寿命对比分析
从以上预测结果可以看出,本文所提组合神经网络方法与单纯采用小波神经网络方法相比,对退化轨迹预测的MSE更小,对剩余寿命的预测精度更高.另外,对比图9和图10中460×102min以后的退化轨迹,小波神经网络的预测结果已经偏离了实际数据的退化趋势,不能给出更长期的预测,而组合神经网络则给出了良好的预测轨迹,具有更长的有效预测距离.
4 结论
本文提出了相关分析和组合神经网络相结合的退化预测方法,并对某电子产品退化数据进行了实际预测验证.主要结论如下:①离散小波变换和自相关分析提供了一种将复杂退化数据,分解成相对简单的有序子序列的途径.②BP和小波神经网络构成的组合神经网络,可以有效发挥两种网络各自的优势,对实际退化序列具有良好的预测效果,具有良好的工程应用前景.
References)
[1] Luo J,Bixby A,Pattipati K,et al.An interacting multiple model approach to model-based prognostics[C]//Proceedings of the IEEE International Conference on Systems,Man and Cybernetics.New York:Institute of Electrical and Electronics Engineers Inc,2003:189-194
[2] Byington C S,Watson M,Edwards D,et al.A model-based approach to prognostics and health management for flight control actuators[C]//2004 IEEE Aerospace Conference Proceedings.New York:Institute of Electrical and Electronics Engineers Inc,2004:3351-3362
[3]周玉辉,康锐,苏荔,等.基于加速磨损试验的止推轴承磨损寿命预测[J].北京航空航天大学学报,2011,37(8):1016-1020 Zhou Yuhui,Kang Rui,Su Li,et al.Life prediction of thrust bearings based on accelerated wear test[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(8):1016-1020(in Chinese)
[4] Biagetti T,Sciubba E.Automatic diagnostics and prognostics of energy conversion processes via knowledge based systems[J].Energy,2004,29(12-15):2553-2572
[5] Liu Y,Li S Q.Decision support for maintenance management using Bayesian networks[C]//2007 International Conference on Wireless Communications,Networking and Mobile Computing.New York:Institute of Electrical and Electronics Engineers Inc,2007:5708-5711
[6] Dong M,He D.Hidden semi-Markov model-based methodology for multi-sensor equipment health diagnosis and prognosis[J].European Journal of Operational Research,2007,178(3):858-878
[7]王小林,程志君,郭波.基于维纳过程金属化膜电容器的剩余寿命预测[J].国防科技大学学报,2011,33(4):146-151 Wang Xiaolin,Cheng Zhijun,Guo Bo.Residual life forecasting of metallized film capacitor based on wiener process[J].Journal of National University of Defense Technology,2011,33(4):146-151(in Chinese)
[8] Zhang S,Ganesan R.Self-organizing neural networks for automated machinery monitoring systems[J].Mechanical Systems and Signal Processing,1996,10(5):517-532
[9] Huang Runqing,Xi Lifeng,Li Xinglin,et al.Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods[J].Mechanical Systems and Signal Processing,2007,21(1):193-207
[10] Gebraeel N Z,Lawley M A.A neural network degradation model for computing and updating residual life distributions[J].IEEE Transactions on Automation Science and Engineering,2008,5(1):156-163
[11] Zhang Q,Benveniste A.Wavelet networks[J].IEEE Transactions on Neural Networks,1992,3(6):889-898

