基于多属性决策的最优路径选择模型＊

任 然 靳文舟 巫威眺

（华南理工大学土木与交通学院 广州 510641）

0 引言

对于在行车过程中寻找1条最优路径问题，传统的交通流诱导系统（TFGS）仅仅只是以最短距离或者最短时间作为单一目标，而在实际驾驶过程中，驾驶员往往权衡各种因素以达到快捷、安全、舒适、高效的出行目的。目前，国内外学者已经提出了不同标准的多种方法来解决此问题，如判定属性权重之间的关系［1］、基于可能度和区间数相离度的多属性决策方法［2］、通过模拟自然界蚂蚁觅食行为的蚁群算法［3］、多约束情况下的路径选择方法［4］，利用各影响因素建立阻抗函数方法［5］、分析各因素的之间相关关系的模糊神经网络算法［6］、以及博弈论［7］、层次分析法、遗传算法等多种最优路径的选择方法。上述研究没考虑驾驶员在路径选择过程中给出的决策值受到驾驶员因素的影响。将最优路径选择过程中所有可能的影响因素（时间、距离、费用、所经交叉路口的多少、所经路况、舒适度、安全性等）纳入考虑，用区间数描述各个属性值，引入反映驾驶员心态的指标［8－10］。

在路径选择过程中，并不是所有的驾驶员对于同样的路径选择问题都有相同的时间、精力，信息处理能力、经验、数据和个人偏好。通过引入心态指标，在多个驾驶员共同决策的基础上建立了1种多属性群决策最优路径选择的新方法，由于心态指标是对单个参与路径选择驾驶员的综合评价值。较之基于偏好的模型，考虑得更为全面，所得到的值更为合理和客观。根据驾驶员不同通过调节心态指标的值就可以得到不同情况下的最优路径，适用性更强。通过算例验证了模型的实用性并且在不同的心态指标下得到了不同的最优路径选择。

1 评价最优路径的各项指标

驾驶员在出行之前要考虑的各种因素，包括时间、距离、费用、所经交叉路口的多少，以及所经路况、舒适度、安全性等。本文将以上因素归纳总结为5 个路径选择评价指标：消耗时间、路径距离、行驶舒适度（包括安全性）、出行费用、路线熟悉度等（路况、交叉口），见图1。选择最优路径这一过程具有不确定性，对于各项指标驾驶员在决策过程中给出的属性值往往不会是1 个精确值［11］，指标之间也会相互影响，各个指标都在一定范围内波动，所以本文用区间数来描述各项指标值。

2 模型的建立

首先设有m 条路径可供选择，记集合为A＝｛A1，A2，…，Ai，…，Am｝；且有n 个评价指标的集合B＝｛B1，B2，…，Bj，…，Bn｝；有d 位驾驶员同时选择，其权重向量为λ＝（λ1，λ2，…，λd）。而各个指标的权重未知，令w＝｛w1，w2，w3，…，wn｝，其中：wj表示评价指标Bj的权重或重要程度，文献［1］对未知属性权重向量之间数学表达式进行了阐释。

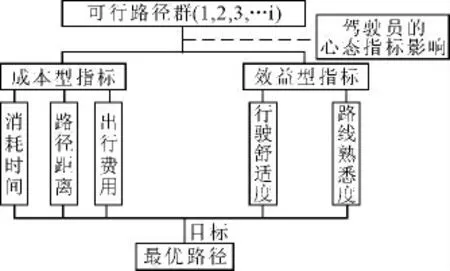
图1 评价指标体系Fig.1 Evaluation index system

2.1 心态指标

在最优路径选择过程中，除去以上确定性指标以外，由于并不是所有的驾驶员对于同样的路径选择问题都有相同的时间、精力、信息处理能力、经验、数据和个人偏好，所以驾驶员心态是路径选择过程中的重要因素，引入心态指标［6］处理驾驶员对各条路径的区间决策值。

定义一：在驾驶员给定区间数a＝［a－，a＋］条件下，基于心态指标t∈［0，1］定义函数

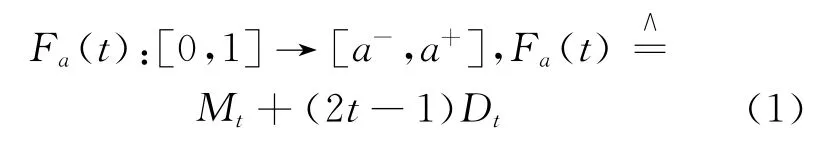
式中：Mt＝0.5（a－ ＋a＋）；Dt＝0.5（a＋－a－）。同时称t为此驾驶员对给出决策区间数a＝［a－，a＋］的心态指标。因为Fa（t）是在［0，1］上的单调递增的函数，所以当t＝0时，Fa（t）＝a－此驾驶员对这条路径的总体路况持悲观态度；t＝1 时，Fa（t）＝a＋此驾驶员对此路径的总体路况持乐观态度。

2.2 最优路径决策过程

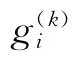
由于各项评价指标的类型不同，对最初的决策矩阵进行一般规范化处理。效益型和成本型分别为

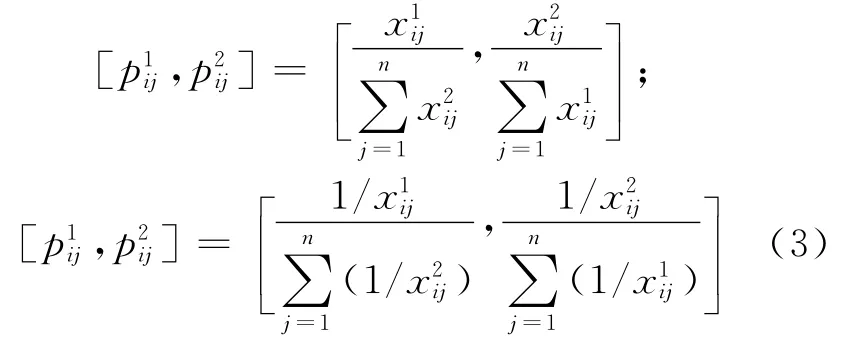
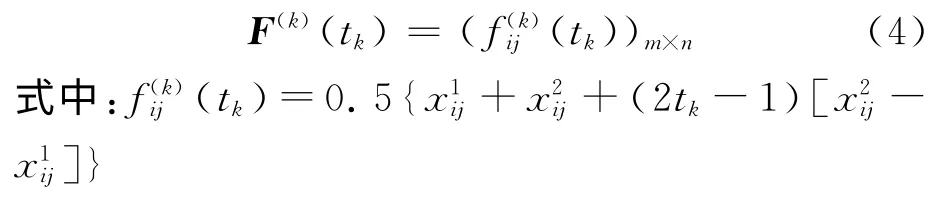
为使所有的驾驶员对最优路径的期望和客观值偏差最小，同时也是每个出行者对路径认识的偏差最小，令Ω为属性权重信息不完全的数学表达式的集合。对于较小区间数值取对数建立多目标规划模型

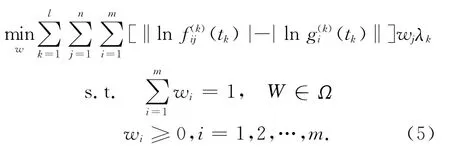
使得每个驾驶员对路径认识的偏差最小。

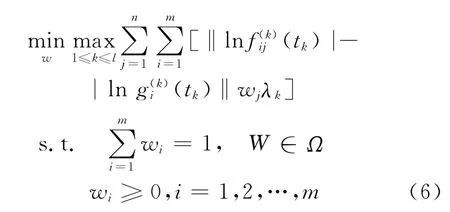
建立多目标非线性规划模型

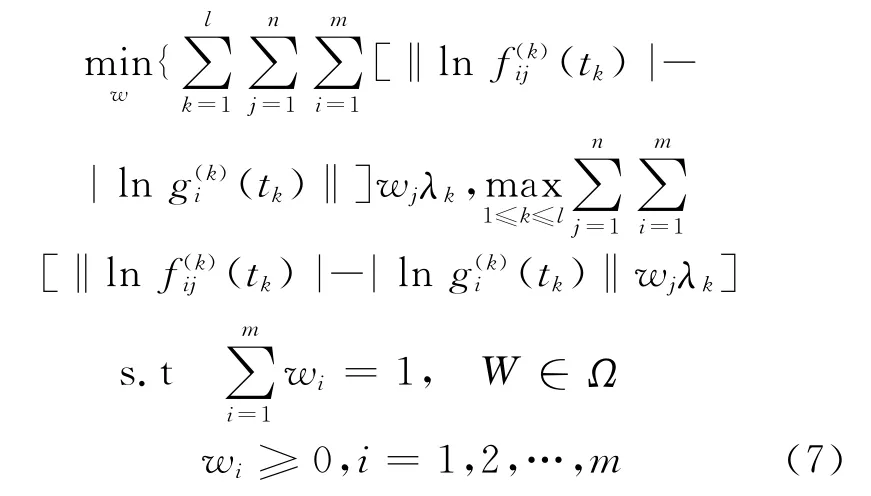
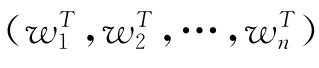
最后，根据驾驶员自身的权重和每个驾驶员对于每条路径的认识值，利用加权平均算子建立每条路径的综合属性值

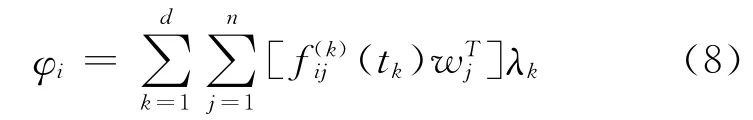
3 算例分析

假设1对OD 之间有3条路径可以选择，有3名驾驶员Ci参与决策，3位驾驶员的权重分别为0.5、0.3、0.2，心态指标分别为0.6、0.54、0.62，对于评价指标不完全权重信息Ω＝（w1≥1.05 w2；w3≥0.09；w2≥2w3；w4＋w5≥0.45；w5≤0.08＋w1），根据以上建模过程叙述，表1给出每个驾驶员在选择路径前对每条路径的主观偏好值。

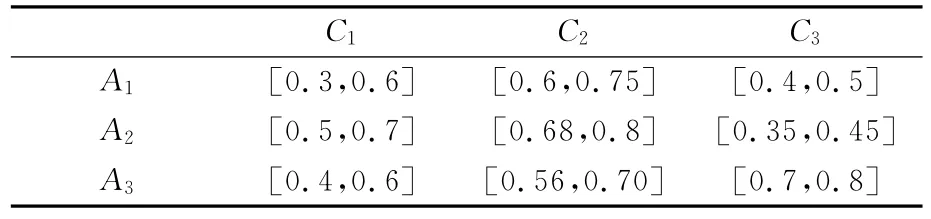
表1 各驾驶员对于每条路径的主观偏好值Tab.1 Each driver＇s preference value for all paths

表2、表3、表4分别给出各条路径的初始值为：

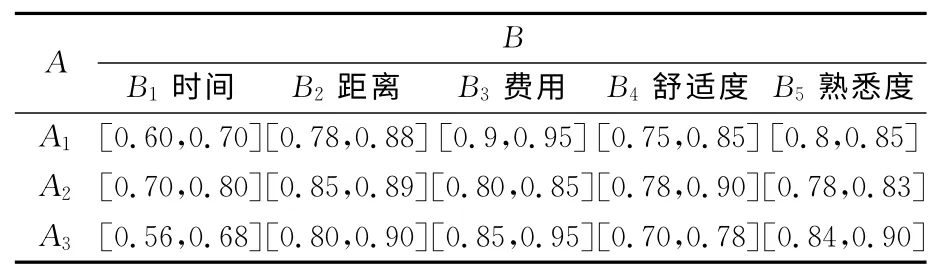
表2 驾驶员C1的初始决策矩阵Tab.2 The first driver＇initial decision－making matrix

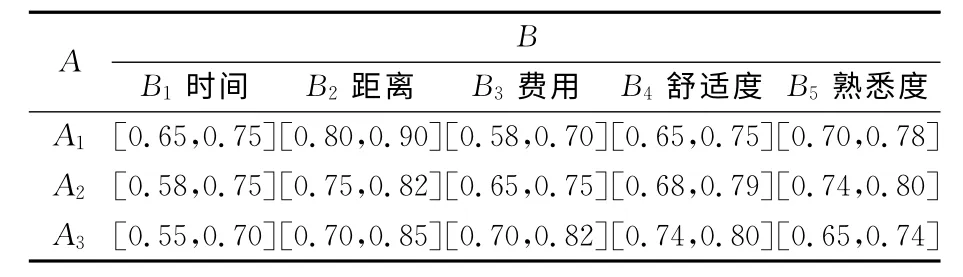
表3 驾驶员C2的初始决策矩阵Tab.3 The second driver＇initial decision－making matrix

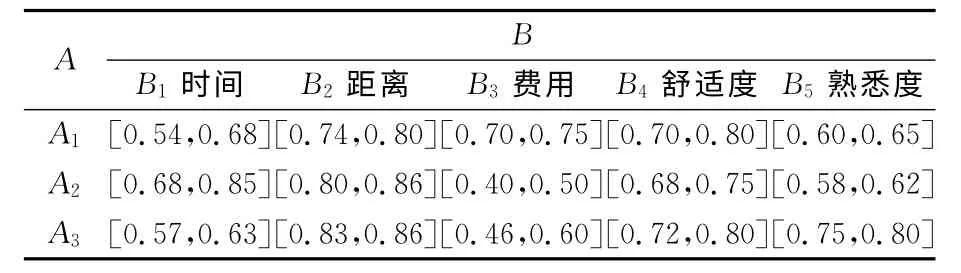
表4 驾驶员C3的初始决策矩阵Tab.4 The third driver＇initial decision－making matrix

对于驾驶员C1给出的以上初始区间值，根据式（2）、（3）进行规范化处理，并利用心态指标式（1）进行处理，得到决策矩阵

同理其他2位驾驶员给出的客观初始认识值经过同样的处理可得决策矩阵

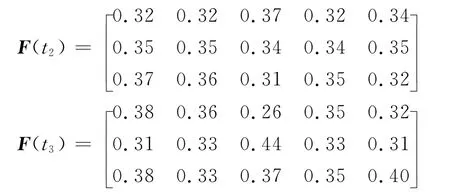
将所有驾驶员的主观认识值和客观认识值经过模型（7）、（8）、（9）并利用Matlab7.0计算得属性权重值为w1＝0.277 92；w2＝0.180 0；w3＝0.090 0；w4＝0.212 3；w5＝0.237 78，由式（10）计算得到各条路径的综合决策属性值φ1 ＝1.019；φ2＝1.005；φ3＝1.060，排序可得：φ3≥φ1≥φ2，那么第3条路径为最优路径。以上结果是在驾驶员心态指标分别是：0.6、0.54、0.62的情况得出的。为了研究不同驾驶员心态影响的结果，设定参数和选择结果见表5：

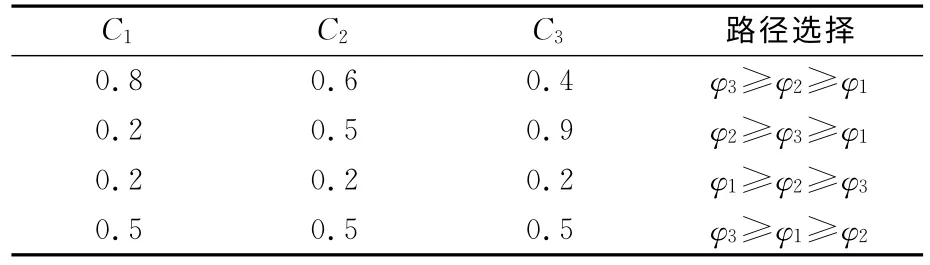
表5 驾驶员心态指标不同的情况下路径选择Tab.5 Path selection under different indicators of drivers＇mentality indicators

可以看出，根据驾驶员不同的心态会得到不同的最优路径结果。特别的，当3个驾驶员都经验不足，时间仓促，对各条路径的情况了解不足，或者开车资历尚浅等原因，路径选择过程中持悲观心态，取心态指标值为0.2，此时最优路径是第1条路径；当驾驶员C1持悲观心态，而驾驶员C2持中庸心态，而驾驶员C3开车经验丰富，对拟选路径给出的信息非常有把握，持激进心态，所以取心态指标值为0.9，此时最优路径是第2条路径。由此可以看出驾驶员决策过程中所持心态不同，对结果存在很重要的影响。

4 结论

相比与其他的最优路径选择方法，本文研建立了1种基于驾驶员心态的多属性群决策最优路径选择模型。并用区间数描述各属性值和设计相应的求解算法，克服了驾驶员自身心态带来的对路径总体评价值的偏差，并能够在客观事实的基础上，尽可能的满足驾驶员主观偏好。在实际运用中，能够根据驾驶员心态不同，适时调节心态指标来选择最优路径。

［1］Ahn B S，Park K S，Han C H，et al.Multi attribute decision aid under in complete information and hierarchical structure［J］.European Journal of Operational Research，2000，125（2）：431－439.

［2］韦增欣，陈进来，罗朝晖.基于驾驶员偏好的最优路径选择［J］.交通运输工程与信息学报，2010，10（6）：141－144.

［3］夏立民，王 华.基于蚁群算法的最优路径选择问题的研究［J］.计算机工程与设计，2007，26（16）：3957－3959.

［4］邹永贵，魏 来.多约束条件的最优路径选择算法研究［J］.计算机应用，2008，28（5）：1101－1103.

［5］王宏仕，许 强.基于驾驶员偏好的最优路径选择方法［J］.交通与安全，2008（12）：176－178.

［6］王 华，夏立民，孟广武.交通最优路径选择算法的对比与仿真［J］.计算机应用软件，2009，26（2）：65－68.

［7］安 实，崔 娜，李 静.基于多智能体博弈的路径选择策略仿真研究［J］.交通信息与安全，2009，27（3）：1－5.

［8］张兴芳，管恩瑞.区间值模糊综合评判及其应用［J］.系统工程理论与实践，2001，12（12）：81－84.

［9］兰 蓉.一种基于区间数距离的理想点多属性决策方法［J］.西安邮电学院学报，2009，14（1）：153－156.

［10］周光明，刘树人.不确定多属性决策中区间数的一种新排序方法［J］.系统工程，2006，24（4）：115－117.

［11］徐国祥.统计预测和决策［M］.上海：上海财经大学出版社，2008（11）.