局部扭转形变下金纳米线的力电响应

贾建明， 孔 静

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

局部扭转形变下金纳米线的力电响应

贾建明， 孔 静

(淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)

采用密度泛函理论和非平衡格林函数方法相结合的研究方案,系统考察了局部扭转形变对金纳米线力电特性的影响．结果表明,随着局部扭转角度的增加,金纳米线的形变区域先后经历了弹性形变和塑性形变;在弹性形变过程中,金纳米线的量子输运特性能够得到很好的保持,伏安特性曲线也不受扭转形变的影响;而在塑性形变中,纳米线的平衡电导和给定电压下的电流均比弹性形变时有显著下降．对输运谱的分析阐明了上述现象的物理机制．

金纳米线; 扭转形变; 力电特性; 密度泛函理论

0 引言

纳米线作为理想的一维体系,因其在纳米电子学和纳机电系统的良好应用前景而受到广泛关注．由于量子限制效应与表面效应,纳米线呈现出许多不同于宏观固体的新奇物理、化学特性,这些新奇特性在直径约3nm以下的超细纳米线中表现得尤为明显．目前,实验上已有许多方法能够制备和获得具有良好结构的多种纳米线．利用电子束辐照金薄膜,通过两端金属点接触之间的窄桥自动细化,在直径0.5～2.0nm、长度3～15nm的悬浮金纳米线中,扫描隧道显微镜就同时观察到了晶状面心立方结构和奇特的螺旋多壳结构[1,2]． 而采用机械控制断裂结方法测量金属纳米线电导时,根据从大量纳米线电导演变曲线构造的电导直方图中出现的特征周期,人们提出了电子和原子壳层效应理论来解释碱金属、贵金属纳米线中出现的稳定结构[3]． 已有的实验与理论结果都表明纳米线的原子结构对于理解它们的物理行为至关重要[4,5]．

所以，昨晚经党小组决议，今天我们要协助国军兄弟一起，把孔志浩送过峡口、杜泽、莲花镇一线，穿越鬼子第三十二师团防区……”

尽管已有大量的实验和理论研究了纳米线的结构特征和力电耦合性质,但大都聚焦在点-面的接触和机械控制的连接断裂,尤其是力学拉伸过程中体系的结构演化与物理性质之间的关联,对稳定结构纳米线在各种形变条件下力电性质的认识还有待进一步探讨．考虑到纳米线在未来纳米电子器件中的应用,深入理解纳米线在局部形变下的结构特征和电输运性质对于器件研发和应用就显得尤为重要．

本文基于第一性原理量子输运计算,系统研究了稳定结构金纳米线在局部扭转形变下的力电特性．结果表明,随着局部扭转角度的增加,金纳米线的形变区域先后经历了弹性形变和塑性形变,直至纳米线完全断裂;在弹性形变过程中,金纳米线的量子输运特性能够得到很好的保持,偏压下的伏安特性曲线也不受扭转形变的影响;然而,在塑性形变中,纳米线的平衡电导和给定电压下的电流均比弹性形变下有显著下降．

1 理论方法

我们选取了沿着[110]晶向,横截面内有4个金原子的金纳米线为研究对象,类似的结构特征和原子排列方式已在各种实验观测中得到确认[5]． 所有关于金纳米线输运性质的计算都是采用了第一性原理程序包ATK, 它结合了密度泛函理论与非平衡格林函数方法．在我们的计算中,对交换-关联势采用了Perdew-Zunger函数形式的局部密度近似,价电子波函数由双ξ极化(DZP)原子轨道基组展开,能量截断为150Ry,k点设置为1×1×100,原子芯电荷由Troullier-Martins非局部赝势描述．通过混合哈密顿量的方法,使得收敛标准达到10-5eV而完成非平衡格林函数与密度泛函理论的自洽计算．

图1 用于研究局部扭转形变下金纳米线力电特性的双探针模型示意图

非平衡格林函数方法在计算电子输运性质时采用了所谓的双探针体系[6-8]． 图1给出了金纳米线作为双探针模型体系的示意图,其中包括左电极、右电极以及中心散射区,而中心散射区也包含了左、右电极的一部分(称为表面层),用以屏蔽中间形变区域对左、右电极的影响．当左、右电极加上电压后,通过中心散射区的电流可以根据如下的Landauer-Büttiker公式求得:

此外，新一轮农地改革政策正在加紧制定。土地承包期再延长30年政策制定工作已启动，不久后将出台。还将深化农村集体产权制度改革，全面开展农村集体资产清产核资、集体成员身份确认，推进集体经营性资产股份合作制改革。资源变资产、资金变股金、农民变股东“三变”改革红利将加快释放。

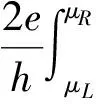
(1)

图2给出了金纳米线在几个典型扭转角度下的结构演变图,其中阴影部分为局部扭转形变中处于表面层和电极区域中扭矩作用下的部分原子．无论是从边视图,还是从顶视图,都可以看出,在扭矩的作用下,形变区域的金纳米线从最初的晶状排列,逐渐发生扭转,出现了螺旋结构;随着扭转角度的增加,形变区域金原子链的螺旋角度不断增大;但当扭转角度超过195°时,纳米线的结构出现了无序变化,直至纳米线完全断开．

金纳米线在局部扭矩作用下的这样一个力学演变过程也可以从其应变能(定义为特定扭转角度下完全结构弛豫后金纳米线的总能与未发生形变时的总能之差)曲线中反映出来(图3)．从图3中可以看出,在扭转角度从0°增加到195°的过程中,纳米线的应变能不断增大,在结构演化上对应着形变区域发生的是弹性形变,也就是说,当扭矩撤销后,整个纳米线能够回复到其未形变(即0°)状态．而当扭转角度超过一定限度(195°)时,应变能出现了突然下降,意味着塑性形变的产生和原子结构的剧烈变化．

大丰收农资商城联合创始人谭泽鑫介绍：“作为一家国内专业的农业互联网服务平台，自2014年成立之初，大丰收就秉承成为农民身边的种植管家的经营理念，围绕农业种植不断深耕和拓展，通过互联网打造农产品产、供、销环节，目前大丰收不仅已经拥有完整的产业链，包含正品农资、科学植保、农产品上行等核心业务，同时形成了线上线下互通互联的立体化服务体系。此次与云图控股的合作，就是希望能把好的产品推荐给农户。”

(2)

我们接着考察了局部扭转形变对金纳米线输运性质和伏安特性的影响．图4给出了纳米线的平衡电导随局部扭转角度的变化关系．可以清楚看出,在0°～195°的弹性形变范围内,尽管形变区域内纳米线的原子结构从晶状向螺旋发生了很大变化,但平衡电导基本保持不变,为3G0．即弹性形变范围内,金纳米线的量子电导特性未受局部形变的影响．但当扭转角度超过195°时,由于塑性形变中原子结构的剧烈变化导致了纳米线的平衡电导明显下降,量子电导现象被破坏,出现了分数电导．

2 结果与讨论

其中,e是电子电荷,h是普朗克常数,f(E,μ)是Fermi-Dirac分布函数．外加在两端电极的电压V会改变左、右电极的化学势μL=Ef-|e|V/2和μR=Ef+|e|V/2(Ef是费米能,|e|V=μL-μR)．对于处于平衡态(外加电压V=0)的体系,其电导G就是透射系数T(E,V)在费米能级Ef处的值,即:

以职业竞争力为导向，以基于工作过程的学习领域课程为核心和主线，以支撑学习领域的平台课程为基础，构建“共性平台课程+专业方向课程+拓展课程”的课程体系，推行“专业竞争力导向的工作过程+支撑平台系统化课程”模式及其开发指导课程的方法，通过多阶段、递进式的组织教学逐步提升学生的职业竞争力。

(左侧为边视图，右侧为顶视图, 阴影部分为局部扭转形变中扭矩作用下的原子)

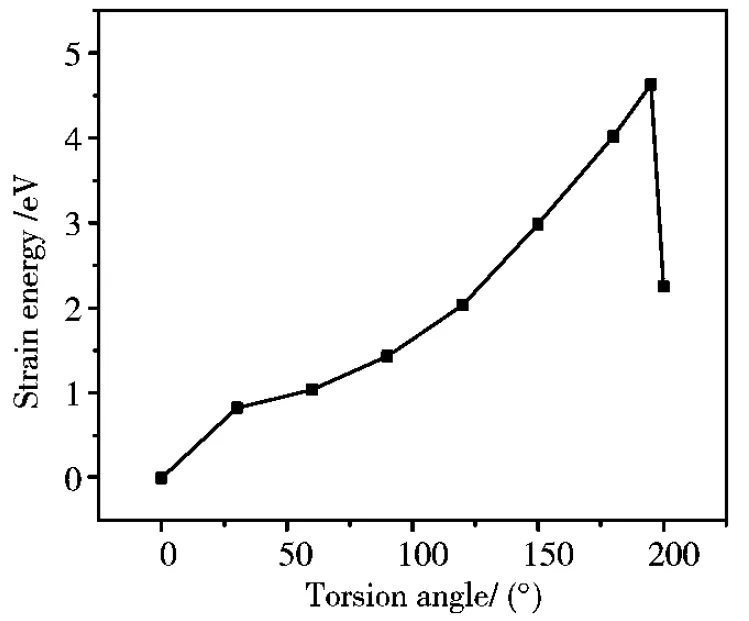
图3 局部扭转形变下金纳米线的应变能随扭转角度的变化关系

图4 局部扭转形变下金纳米线平衡电导随扭转角度的变化关系

为了进一步探究局部形变的影响,图5给出了3个典型扭转角度(90°,195°和200°)下金纳米线的零偏压输运谱(其中费米能级设为0eV)．作为参照,图中也给出了未发生形变时,晶状金纳米线的输运谱曲线．可以看出,晶状金纳米线台阶状的输运曲线表现出其良好的量子电导特性,在费米能(0eV)附近的输运系数为3．随着电子能级的变化,能带结构中输运通道的变化将导致相应输运系数的改变．当纳米线发生局部扭转形变时,整个输运谱也受到了影响．只是在弹性形变范围内,输运谱的变化主要体现在距离费米面较远的能量区域中,随着扭转角度的增加,输运曲线的强度逐渐减弱,而费米能附近的输运曲线变化不大．但当纳米线出现塑性形变后,如图5中的Torsion-200°所示,输运曲线在整个能量区间内发生了明显变化,相比较于未形变时,强度均有显著下降,并且台阶状的量子电导特性也完全消失．

总之，培养留守儿童良好的学习习惯需要家庭、学校、社会同关注、齐参与，我们教师作为留守儿童的“家庭外监护人”，在他们的家庭教育缺失的情况下，要通过不断地探索，让他们感受到教师的关爱，培养他们的自信心、自尊心，培养他们的自主学习的习惯，让他们在初中三年的学习和生活中温暖、充实、有收获。

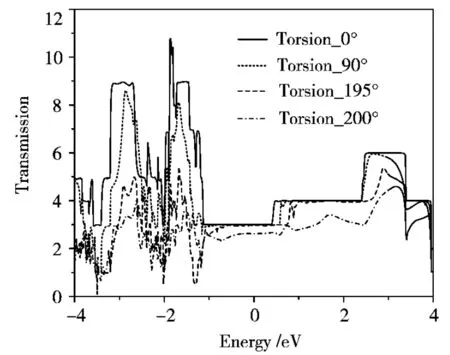
图5 不同扭转角度下金纳米线的零偏压输运谱

图6 不同扭转角度下金纳米线的伏安特性曲线

图6进一步描述了局部扭转形变对一定电压范围内金纳米线的伏安特性曲线的影响．可以看出,纳米线的伏安特性曲线在形状上表现出两段斜率不同的线性关系．但值得注意的是,在弹性形变内(0°～195°),两个斜率值与扭转角度无关,即纳米线的伏安特性不受局部扭转区域内原子结构变化的影响．而当塑性形变出现后(gt;195°),虽然两段不同斜率的线性关系继续保持,但一定电压下,塑性形变时纳米线中的电流明显小于弹性形变时的值,这主要是由于塑性形变所引起的输运系数总体下降造成的．

图7 未发生扭转(a)与局部扭转200°(b)时不同电压下金纳米线的输运谱

为了探究金纳米线伏安特性曲线上所表现出的两段斜率不同的线性关系,图7中画出了未发生形变(0°)和发生塑性形变(200°)后不同电压(0.5,1.0,1.5和2.0V)下金纳米线的输运谱(费米能级设为0eV，阴影区域表示偏压窗口)．根据Landauer-Büttiker公式(式(1)),由左、右电极化学势μL和μR构成的能量积分区间,通常被称为偏压窗口(图7中阴影区域)．在未发生形变时(图7a),随着金纳米线两端所加电压逐渐增大,纳米线的输运谱也随之逐渐向右平移,但在0～1.0V的范围内,都只有数值为3的相同的一段输运曲线处于偏压窗口内,导致电流随着电压的增加(偏压窗口的增大)线性增加;而当电压gt;1.0V时,由于输运谱的右移,部分数值为2的输运曲线移进了偏压窗口,尽管随着电压的增大,电流依然增加,但其增加幅度都比0～1.0V时有所减小,导致斜率不同的伏安特性曲线出现．当金纳米线发生塑性形变后(图7b),同样由于电压引起的输运曲线平移,出现了两条斜率不同的伏安特性线性关系,但因为塑性形变下的输运系数小于未形变和弹性形变情形,所以两个斜率的数值均有所降低．

3 结论

综上所述,我们采用密度泛函理论和非平衡态格林函数方法相结合，系统考察了局部扭转形变对金纳米线力电特性的影响．我们观察到,尽管局部扭矩能够引起金纳米线形变区域原子结构的明显变化,但只要在弹性限度内,纳米线的输运性质和伏安特性基本不受影响;而当扭转形变超出了弹性范围,不仅纳米线的规则结构受到破坏,相应的输运特性也发生了明显变化．我们的理论结果给出了局部扭矩作用下金纳米线力电特性的完整图像,对于纳米线在未来纳米电子器件中的应用也具有参考意义．

[1] Kondo Y, Takayanagi K. Gold nanobridge stabilized by surface structure[J]. Physical Review Letters, 1997, 79(18): 3455-3458.

[2] Kondo Y, Takayanagi K. Synthesis and characterization of helical multi-shell gold nanowires[J]. Science, 2000, 289: 606-610.

[3] Mares A I, Ruitenbeek J M. Observation of shell effects in nanowires for the noble metals Cu Ag and Au[J]. Physical Review B, 2005, 72(20): 205402(1-7).

[4] Rodrigues V, Fuhrer T, Ugarte D. Signature of atomic structure in the quantum conductance of gold nanowires[J]. Physical Review Letters, 2000, 85(19): 4124-4127.

[5] Hong B H, Bae S C, Lee C, et al. Ultrathin single-crystalline silver nanowire arrays formed in an ambient solution phase[J]. Science 2001, 294: 348-351.

[6] Brandbyge M, Mozos J L, Ordejan P, et al. Density-functional method for nonequilibrium electron transport[J]. Phys Rev B, 2002, 65(16): 165401(1-17).

[7] Soler J M, Artacho E, Gale J D, et al. The SIESTA method for ab initio order-N materials simulation[J]. J Phys: Condens Matter, 2002, 14(11): 2745-2779.

[8] Taylor J, Guo H, Wang J. Ab initio modeling of quantum transport properties of molecular electronic devices[J]. Phys Rev B, 2001, 63(24): 245407(1-13).

[9] Delley B. An all-electron numerical method for solving the local density functional for polyatomic molecules[J]. J Chem Phys, 1990, 92(1): 508-517.

[10] Delley B. From molecules to solids with the DMol3approach[J]. J Chem Phys, 2000, 113(18): 7756-7764.

ElectromechanicalResponseofGoldNanowireunderLocalTorsionalDeformation

JIA Jian-ming, KONG Jin

(School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)

The mechanical and electrical properties of gold nanowire under local torsional deformation have been investigated using a combined formalism of density functional theory and nonequilibrium Green's function. It is shown that with increasing torsional angle, the deformed region of nanowire undergoes the elastic and plastic deformation. During the elastic deformation, the transport properties of nanowire can be retained very well, while the plastic deformation has a significant effect on the conductance value and the current-voltage characteristic. The underlaid physical mechanism is discussed.

gold nanowire; torsional deformation; electromechanical property; density-functional theory

2013-03-16

贾建明(1972-), 男, 江苏扬州人, 副教授, 博士, 主要研究方向为纳米物理及计算材料学.

TB383.1

A

1671-6876(2013)02-0120-05

[责任编辑蒋海龙]