基因识别中信噪比与功率谱的快速计算公式及算法实现
郭丽娜, 郭俊峰
(1.南京财经大学 应用数学学院, 江苏 南京 210023; 2.南京财经大学 经济学院, 江苏 南京 210023)
基因识别中信噪比与功率谱的快速计算公式及算法实现
郭丽娜1, 郭俊峰2
(1.南京财经大学 应用数学学院, 江苏 南京 210023; 2.南京财经大学 经济学院, 江苏 南京 210023)
DNA序列信号频谱3-周期性是一个被广泛用于区分编码区和非编码区的重要特征,根据核苷酸中3个密码子位置的不均衡性,给出了功率谱与信噪比的快速计算公式. 研究发现快速计算公式有助于基因识别的实现,为探测内含子、外显子提供了一个快速高效的方法.
信噪比; 功率谱; 基因识别; 外显子; 内含子
0 引言
基于海量的人类及其他生物基因组数据,对基因进行识别是生物信息学的一项重要研究课题[1]. 利用计算机分析和研究核苷酸序列,对蛋白质编码区的位置、结构和功能进行注释是基因识别的主要内容,其研究又分为两大类:蛋白质编码区识别和功能位点识别[2-3].目前这两方面的研究都不是非常令人满意,关于基因编码区的识别,特别是对较短序列的预测效果仍然不理想.在面对大量、复杂的基因序列数据时,如何更好更快地获取准确的基因信息,如何在众多的基因序列中确定功率谱和信噪比,如何快速实现基因识别算法,是我们面临的一项重要课题.
在生物学、医学、药学等诸多方面,对DNA的研究具有重要的理论意义与实际价值.对于较长的DNA序列,应用离散Fourier变换(Discrete Fourier Transform,简称DFT变换) 计算其信噪比或功率谱时总体计算量很大,会影响到所设计的基因识别算法的效率[4].鉴于此,文中基于Voss映射,给出对于任意映射下功率谱与信噪比的快速计算公式.
1 数字序列映射
在DNA序列研究中,首先需要把A、T、G、C这4种核苷酸的符号序列,根据一定的规则映射成相应的数值序列,以便于对其作数字处理.
令I={A,T,G,C},长度(即核苷酸符号个数,又称碱基对(Base Pair)长度,单位记为bp)为N的任意DNA序列,可表达为
S={S[n] |S[n]∈I,n=0,1,2,…N-1},
即A、T、G、C的符号序列S:S[0],S[1],…,S[N-1].现对于任意确定的b∈I,令
称之为Voss映射[1],于是生成相应的0-1序列(即二进制序列){ub[n]}:ub[0],ub[1], …,ub[N-1](b∈I).
例如,假设给定的一段DNA序列片段为S=ATCGTACTG,则所生成的4个0-1序列分别为:
{uA[n]}:{1,0,0,0,0,1,0,0,0}; {uG[n]}:{0,0,0,1,0,0,0,0,1};
{uC[n]}:{0,0,1,0,0,0,1,0,0}; {uT[n]}:{0,1,0,0,1,0,0,1,0}.
这样产生的4个数字序列又称为DNA序列的指示序列(indicator Sequence).
2 功率谱与信噪比
为研究DNA编码序列(外显子)的特性,对指示序列分别做离散Fourier变换(DFT)

以此可得到4个长度均为N的复数序列{Ub[k]},b∈I.计算每个复序列{Ub[k]}的平方功率谱,并相加则得到整个DNA序列S的功率谱序列{P[k]}:
P[k]=|UA[k]|2+|UT[k]|2+|UG[k]|2+|UC[k]|2,k=0,1,…N-1
对于同一段DNA序列,其外显子与内含子序列片段的功率谱通常表现出不同的特性
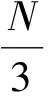

图1 编号为BK006948.2的酵母基因DNA序列的功率谱
记DNA序列S的总功率谱的平均值为
(1)


(2)
DNA序列的信噪比值的大小,既表示频谱峰值(Peak Value)的相对高度,也反映编码或非编码序列3-周期性的强弱.
信噪比R大于某个适当选定的阈值R0(比如R0=2),是DNA序列上编码序列片段(外显子)通常满足的特性,而内含子则一般不具有该性质[2].
3 基于核苷酸分布频率的信噪比与功率谱的快速计算公式
3.1 基于密码子中核苷酸分布频率的平均功率谱的快速计算公式
对A→0,C→1,G→2,T→3这种类型的实数映射,其目的是为了继续对核苷酸序列信息转换进行降维,从而提高计算功率谱与信噪比的速度.但是,基于映射建立的信噪比和功率谱的计算量仍然很大,根据核苷酸中3个密码子位置的不平衡性,可以通过分析核苷酸序列的频率分布来建立信噪比与功率谱的快速计算公式.

(3)
其中σF是密码子3个位置处核苷酸频率的方差,记作:
(4)

(5)
则可得功率谱的快速计算公式:

(6)
3.2 基于密码子中核苷酸分布频率的信噪比的快速计算公式

(7)

因而DNA序列的功率谱峰值:
(8)
二次型的系数矩阵M为半正定阵,其特征值分别为1.5、1.5、0,且当Fx1=Fx2=Fx3时,功率谱值为0.因此,当碱基在序列的3种位置上的频数(Fx1,Fx2,Fx3)分布偏差越小时,功率谱曲线的峰值P(N/3)越接近于0.功率谱峰值实际上反映了基因密码子出现的某种概率不均衡性.
大量的计算实验表明[3],一个没有错误符号的长度为N的DNA序列的总功率为:
(9)

(10)
3.3 数值实验
本段均选取线虫粘粒(AF100306)及人的线粒体全基因组(NC-012920)的第3个基因片段进行实验. 分别用原始的信噪比、功率谱计算式(1)、式(2)及文中改进的快速算法式(6)、式(10)来进行求解. 应用Matlab 7.0运行结果如表1和表2所示.

表1 基于两种算法下线虫粘粒的DNA序列所对应的信噪比

表2 基于两种算法下人的线粒体全基因组的DNA序列所对应的信噪比
线虫粘粒基于原始的功率谱计算公式所得图形如图2所示,由图2可看出线虫粘粒的这段基因序列不具有双峰结构.并且由表1可看出,对于内含子基因片段,运用快速算法计算的信噪比较之于原始算法更小,根据阈值的计算原理,可排除该基因片段是外显子的可能性.
人的线粒体全基因组基于原始的功率谱计算公式所得图形如图3所示,由图3可以看出人的线粒体全基因组具有双峰结构,而人们通常都是根据基因序列的功率谱图是否具有双峰结构来判别是否是外显子区域.但由表2发现,运用原始算法计算的信噪比值较之于快速算法更小,根据阈值的计算原理可知,从一定程度上运用原始算法在识别基因外显子区间时将会产生误差,会扩大外显子区间,将原本内含子的部分误认为是外显子.由此,可发现快速计算公式有助于基因识别的实现,为探测内含子、外显子提供了一个快速高效的方法.

图2 线虫粘粒的功率谱图

图3 人的线粒体全基因组的功率谱图
4 结论
本文根据DNA序列3-周期性,得到了功率谱与信噪比的快速计算公式,使之更具有广泛性和适用性. 并且研究发现快速计算公式有助于基因识别的实现,为探测内含子、外显子提供了一个快速高效的方法.
[1] Rushdi A, Tuqan J. Gene identification using the Z-curve representation[J]. Department of Electrical and Computer Engineering University of California, 2006, 2(2): 1024-1027.
[2] Yin C C, Yau S T. Prediction of protein coding regions by the 3-base periodicity analysis of a DNA sequence[J]. Journal of Theoretical Biology, 2007, 247(4):687-694.
[3] 邵建峰,严晓华,邵伟,等. DNA序列信号3-周期特性[J]. 南京工业大学学报,2012,7(4):134-137.
[4] Chang H, Stephen S Y. A fourier characteristic of coding sequences: origins and a non-fourier approximation[J]. Journal of Computational Biology, 2005, 12(9):1153-1165.
[5] Sharma S, Doherty K M, Brosh R M. Mechanisms of RecQ helicases in pathways of DNA metabolism and maintenance of genomic stability[J]. Biochem J, 2006,398:319-337.
[6] 马宝山. 基于信号处理理论和方法的基因预测研究[D]. 大连:大连海事大学, 2008.
[7] 田元新, 陈超, 邹小勇, 等. 外显子周期三行为特征的研究[J]. 化学学报, 2005, 63: 1215-1219.
[8] 杨莉. DNA序列4D表示及基因识别算法研究[D]. 长沙: 湖南大学博士论文, 2005.
[9] Burge C, Karlin S. Prediction of complete gene structures in human genomic DNA[J]. Mol Biol, 2007, 268:78-94.
[10] Berryman M J, Allison A. Review of signal processing in genetics[J]. Fluctuation and Noise Letters, 2005, 5(4):13-35.
[11] Koltar D, Lavner Y. Gene prediction by spectral rotation measure: a new method for identifying protein-coding regions[J]. Genome Res, 2003, 13: 1930-1937.
[12] Guan M X. Mitochondrial DNA mutations associated with aminoglycoside ototoxicity[J]. Journal of Otology, 2006:65-75.
[13] 郭烁. DNA信号序列分析的基因预测方法研究[D]. 大连: 大连海事大学,2010.
[14] 杨莉. DNA序列4D表示及基因识别算法研究[D]. 长沙: 湖南大学, 2007.
TheFastCalculationFormulasandAlgorithmsofSignalNoiseRatioandPowerSpectruminGeneIdentification
GUO Li-na1, GUO Jun-feng2
(1.School of Applied Mathematics Nanjing University of Finance and Economics, Nanjing Jiangsu 210023, China)(2.School of economics, Nanjing University of Finance and Economics, Nanjing Jiangsu 210023, China)
The 3-periodicity is well acknowledged as an important feature that can be used for distinguishing gene coding regions of a DNA sequence. According to the asymmetric distribution of each of the four bases among the three codon positions, we draw the fast calculation formulas of signal noise ratio and power spectrum. It turned out that the fast calculation formulas can contribute to gene identification, and provide a fast and effective method to the prediction of intron and exon
signal noise ratio; power spectrum; gene identification; extron; intron
2013-02-05
江苏省高校研究生科研创新项目(2012CXLX1)
郭丽娜(1989-), 女, 江西吉安人, 硕士研究生, 研究方向为分形与小波理论.
O212.1
A
1671-6876(2013)02-0110-05
[责任编辑李春红]

