基于函数型数据分析方法对心电图中T波与RR间期的研究
杨恋波, 袁 媛
(马鞍山师范高等专科学校, 安徽 马鞍山 243041)
基于函数型数据分析方法对心电图中T波与RR间期的研究
杨恋波, 袁 媛
(马鞍山师范高等专科学校, 安徽 马鞍山 243041)
心电图(ECG)一般是由P,Q,R,S,T等5个波组成.每个波代表着一定的心动信息,并且各个波之间存在一定的联系.利用函数型数据分析的方法,建立了心电图中T波与RR间期的函数型线性回归模型.求解模型以及检验模型的结果表明了函数型线性回归模型能较好地反映T波与RR间期的关系.
函数型线性回归模型; T波; RR间期; 函数型数据分析
0 引言
心电图(简称ECG)是指心脏在每个心动周期中,由起搏点、心房、心室相继兴奋,伴随着生物电的变化,通过心电描记器从体表引出多种形式的电位变化所形成的图形.心电图对研究心脏基本功能及其病理等方面具有重要的参考价值.心电图一般是由P,Q,R,S,T等5个波组成,有时还包括U波,如图1所示.

图1 心电图波型示意图
在临床上,每个波代表着一定的心动信息,这些信息能够很好地反映心脏的病变情况.例如,P波的宽度不超过0.11s,振幅不超过0.25mV.当P波的振幅和宽度超过上述范围时即为异常,常表示心房肥大.Q波的振幅不得超过同导联R波的1/4,时间不超过0.04s,超过正常范围的Q波称为异常Q波,常见于心肌梗塞等.T波钝圆,占时较长,从基线开始缓慢上升,然后较快下降,形成前肢较长、后肢较短的波形.当T波低平或倒置时,常说明有心肌缺血、低血钾等症状.因此,在临床实验的有关文献中,通常用分析心电图中的单个波或其组合的方法来研究心脏的病变情况.
目前常用的方法是研究QT间期及其与RR间期之间的关系,且得到了比较多的结论[1].但由于QT间期的取值跟Q波的起点和T波的终点相关,而目前对于判断T波终点并没有很好的方法,一般是通过人工确定T波的终点,这往往会产生比较大的误差,而且这种方法的成本也很高.同时QT间期跟RR间期的关系对于不同的受试对象或不同数目的数据,也不是很稳定,没有固定的结论.而T波是心室复极顺序发生细微变化的敏感指标,且从心电图(图1)中可以看出,T波嵌套在一个RR间期中,同时其波形具有比较明显的特征.更重要的是T波值可以通过仪器自动采集,并且能得到一条完整的T波信息,避免产生一些不必要的误差.同时随着科学技术的发展,T波的采样值也越来越精确,T波的采样值可近似地看成关于时间的函数[2,3].所以,本文试图通过函数型数据分析的方法,将T波的采样值转换成函数型数据,建立T波与RR间期的函数型线性回归模型,来研究两者之间的关系[4-6].
1 数据的获得及函数型线性回归模型的建立求解
为了能充分利用完整的心电图数据,以及理解T波的变化,此研究将在连续心跳的心电图中截取相关的T波及RR间期数据.采样的T波数据为一个矩阵Y=(y1,…,yI),yi=(yit1,…,yitJ)′,i=1,2,…,I.yitj表示第i次心跳中的第tj个时间点的T波采样值(j=1,2,…,J).RR间期数据为一个向量X=(x1,…,xI).

图2 受试对象部分心电图像
本文将对单个受试对象的T波与RR间期关系进行研究.由于数据较多,先选择其中一人的数据来作讨论和分析,其部分心电图如图2所示.对图2中心电图的采样数据进行处理,从中得到他的RR间期和T波的数据,其中RR间期数据对应的图像见图3,T波对应的图像见图4(T波图像中的横坐标时间t(0∶60)表示从每次心跳中得到60个T波采样数据所对应的时间).

图3 受试对象的RR间期按心跳顺序的数据图

图4 受试对象的T波数据三维图
为了求解函数型线性回归模型,把T波的采样值进行函数化处理[3],使其转换成函数型数据.处理后,T波的函数型数据可记为:
y=(y1(t),y2(t),…,yn(t))
这些数据对应的图像为图5.
建立基于上述RR间期数据和T波函数型数据的函数型线性回归模型,即:
yi(t)=c(t)+β(t)xi+εi(t), (i=1,2,…,n)
(1)
其中,yi(t)代表受试对象第i个心跳中的T波的函数型数据;c(t)是类似于线性回归分析中的回归常数β0,是一常数型函数;β(t)是函数型回归系数;εi(t)是随机误差函数.
将获得及处理后的数据代入函数型线性回归模型(1),利用Matlab求解得到其回归系数,其结果可用图像表示,如图6所示.

图5 受试对象的T波函数型数据

图6 受试对象的函数型回归系数
2 模型的检验与结果分析
为了检验模型的优劣,结合多元线性回归模型中的SSE以及R2等概念来对函数型线性回归模型的结果进行检验和分析.由此建立函数型线性回归模型中的SSEi,具体如下:
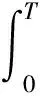
(2)

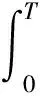
(3)

(4)

图7是受试对象的SSE值.如果SSE接近于0,说明模型选择和拟合程度好,数据预测也成功.从图7中可以看出,SEE的值只有在开始的一段偏大,从第3个心跳开始,各个心跳的SSE值均低于0.2487,说明模型(1)具有较好的拟合和预测效果.

图7 受试对象的SSE值

图8 受试对象的R2值
图8为受试对象的R2值的图像.对于R2而言,它的正常取值范围为[0,1], 其值越接近1,表明方程的变量对y的解释越强.从图8中可以看出,R2的值只有开头一段比较小,从第3个心跳开始,其值均大于0.8173,说明模型(1)中的RR间期对T波数据的解释能力较强.
除了对受试对象的数据进行处理外,还对其他受试对象的数据进行了研究和分析,所得结果基本类似.因而,本文利用函数型线性回归模型来讨论心电图中T波与RR间期之间关系的方法是可行的.通过求解、分析和检验,该函数型线性回归模型能较好反映这两者之间的关系,即说明心电图中的T波数据,可以由RR间期数据通过某个函数型线性回归模型来表示.这为研究心电图数据提供了一种新的途径.
[1] Dmitrienko A, Smith B. Repeated-measures models in the analysis of QT interval[J]. Pharmaceutical statistics, 2003,2:175-190.
[2] Zhou Y C, Sedransk N. Functional data analytic approach of modeling ECG T-wave shape to measure cardiovascular behavior[J]. The Annals of Applied Statistics, 2009, 3(4):1382-1402.
[3] 吕安康, 沈卫峰. T波形成机制与T波改变的分类及临床意义[J]. 临床心电学杂志, 2000,8:131-132
[4] Ramsay J O, Silverman B W. Functional Data Analysis[M]. 北京:科学出版社, 2006.
[5] 严明义. 函数性数据的统计分析:思想、方法和应用[J]. 统计研究, 2007, 2:87-94.
[6] 何晓群, 刘文卿. 应用回归分析[M].2版. 北京:中国人民大学出版社, 2007.
AFunctionalDataAnalysisforStudyingtheRelationofECGT-waveandRRIntervals
YANG Lian-bo, YUAN Yuan
(Maanshan Teachers College, Maanshan Anhui 243041, China)
Electrocardiogram (ECG) consists of P, Q, R, S, T. Each wave represents certain heart activity, and there is some connection between them. This paper, by using functional data analysis method, we established a functional linear model to analyze T-wave and RR interval of the ECG. By solving the model, and testing the model’s results, this paper explains the functional linear model can well reflect the relation between the T-wave and RR interval.
functional linear model; T-wave; RR interval; functional data analysis
2013-01-05
安徽省高校自然科学基金资助项目(KJ2013Z313)
杨恋波(1982-), 男, 浙江诸暨人, 讲师, 硕士, 研究方向为概率统计.
O212.1
A
1671-6876(2013)02-0125-04
[责任编辑蒋海龙]

