多目标优化问题中解的一些性质

蒋 娅

(西华师范大学 数学与信息学院, 四川 南充 637002)

多目标优化问题中解的一些性质

蒋 娅

(西华师范大学 数学与信息学院, 四川 南充 637002)

借助多目标最优化问题中解的几个基本概念,得出了不同解之间的一些基本性质．这些性质将为更好地研究多目标优化问题提供理论基础．

多目标规划; 绝对最优解; 有效解; 弱有效解

0 引言

多目标规划是运筹学和决策科学的一个交叉学科分支,是近年来发展起来的新学科．它研究在一定的约束条件下多个目标函数的极值问题．在现实生活中,人们经常会遇到同时追求多个目标的最优化问题．例如,设计一个新产品,人们总希望在一定条件下,能选择同时具有质量好、产量高和利润大的方案．这类在给定条件下,同时要求多个目标都尽可能好的最优化问题,称为多目标最优化问题．研究多目标最优化问题的学科称为多目标最优化或多目标规划(multiobjective programming)．它是数学规划的一个重要分支,其理论和方法在经济规划、计划管理、金融决策、工程设计、城市与工农业规划、卫生保健和军事科学等领域中有着广泛的应用．本文主要借助多目标最优化问题中解的几个基本概念,得出了不同解之间的一些基本性质．这些性质将为更好地研究多目标优化问题提供理论基础．

1 基本概念

考虑多目标最优化问题:

(1)

其中X⊂Rn,fk:X→R(k=1,…,m),gi:X→R(i=1,…,p),hj:X→R(j=1,…,q),均为定义在X上的可微连续函数,D表示(1)的可行集,即:

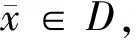
定义2[2]设α=(a1,…,am)T和β=(b1,…,bm)T是m维向量．

1) 若ai=bi(i=1,…,m),则称向量α等于向量β,记作α=β．

2) 若ai≤bi(i=1,…,m),则称向量α小于等于向量β,记作α≤β或β≥α．

3) 若ai≤bi(i=1,…,m),并且其中至少有一个严格不等式成立,则称向量α小于向量β,记作αβ或β≻α．

4) 若ailt;bi(i=1,…,m),则称向量α严格小于向量β,记作αlt;β或βgt;α．

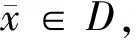
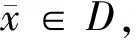
2 主要结论

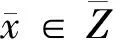
定理2 有效解必为弱有效解,即:P⊆Pw

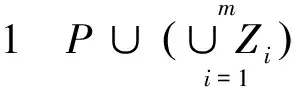
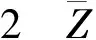
[1] 解可新, 韩健, 林友联. 最优化方法[M].天津:天津大学出版社,2004.

[2] Mangasarian O L.Nonlinear Programming[M].New York:MC Gravy Hill,1969.

[3] 魏权龄, 王日爽. 数学规划与最优化[M]. 北京: 国防科学出版社. 1984.

[4] 林锉云, 董加礼. 多目标优化的方法与理论[M]. 北京:高等教育出版社. 1992.

[5] 胡毓达. 多目标规划有效性理论[M]. 上海: 上海科学技术出版社. 1989.

SomePropertiesofSolutioninMultiObjectiveProblem

JIANG Ya

(College of Mathematics and Information, China West Normal University, Nanchong Sichuan 637002, China)

Multi-objective programming is a cross discipline branch of operational research and decision-making science, which is a new discipline in recent years. It studies extreme value problem under certain constraints to a number of objective function. This paper uses several concepts of solution in multi-objective optimization problem, and the author obtains some basic properties between different dissociations.These properties will provide a theoretical basis for the better study of multi objective optimization problems

multiobjective programming; absolutely optimal solutions; effective solutions; weakly effective solutions

2013-01-09

蒋娅(1982-), 女, 四川广安人, 讲师, 硕士, 研究方向为优化理论及应用.

O224

A

1671-6876(2013)02-0115-02

[责任编辑李春红]