城市交通事故对道路通行能力影响模型
胡 宏
(淮阴师范学院 数学科学学院, 江苏 淮安 223300)
城市交通事故对道路通行能力影响模型
胡 宏
(淮阴师范学院 数学科学学院, 江苏 淮安 223300)
用M/G/1排队系统理论分析了交通事故发生后交通堵塞与道路通行能力、路段上游车流量的关系,并建立了数学模型.利用这一模型可以对堵塞时的车队长度进行计算.
泊松过程;M/G/1排队系统; 伽玛分布; 指数分布; 参数估计
0 引言
在城市交通中,由于交通事故、路边停车及占道施工等因素,经常会导致车道或道路横断面通行能力在单位时间内降低.由于城市道路交通流密度大、连续性强,一条车道被占用,往往会影响其他车道的通行,从而降低路段所有车道的通行能力.即使事故造成的停车时间短,也可能引起车辆排队,出现交通阻塞. 如果事故处理不当,经常引起长时间拥堵,进而引起整个区域的交通阻塞.
车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影响程度,会为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案等提供理论依据.
对于道路阻塞时的车辆排队长度已经有了一些计算方法[1-4].在本文中,我们将运用排队论方法构建数学模型,分析交通事故对事故发生路段车辆排队长度与事故横断面实际通行能力的影响,并估计事故前后路段上游堵塞车辆的程度.
1 交通事故时道路阻塞模型
1.1 模型假设
(H1) 在 [0,t)内到达事故区域车辆数X(t)服从参数λ(>0)为的泊松过程;
(H2) 每辆车通过事故横断面的时间(接受服务时间)是独立同分布的随机变量,其共同的分布为参数为μ(>0)的指数分布,分布函数记为G(x).
据以上分析,所研究问题可以看成M/G/1排队系统问题[1].
假设发生交通事故时, 原道路只有一个车道可以通行,此时可看成是只有一个服务员的服务站,而车辆通过事故现场横断面的过程可以看作是得到服务的过程,车辆排队等候通过横断面的过程可以看作是等候服务的过程.
1.2 模型的建立
我们用M/G/1排队系统理论研究交通事故发生时的道路交通问题.设Xn表示第n辆车接受服务后剩下的车辆数,Yn表示第n+1辆车接受服务期间到来的车辆数.当Xn>0时,表示系统在第n辆车离开后,剩下的Xn辆车中有一辆车进入服务,而其余Xn-1辆车在排队等候,因此下一辆车离去时,系统中的车辆数为排队的Xn-1辆车及第n+1辆车接受服务期间到来的车辆数之和,当Xn=0时,类似讨论.由此可得
(1)
由于{Yn}n≥1是不相重叠的服务时间中到达系统的车辆数,由泊松过程的性质知它们相互独立,且有共同分布[5,6],则
(2)
由(1)和(2)知{Xn}n≥1是马尔可夫链,进一步据假设(H1)和(H2),其转移概率为
(3)
由数学期望定义知,在一个服务周期内来到系统车辆的数学期望为
(4)
将G(x)=1-e-μx代入有

从而有

(5)

1.3 模型参数的估计
对实际发生的交通事故,我们可以根据事故前后车道中通行的车辆数和通行情况的数据来估计参数λ和μ的大小.这一数据可以通过一些监控视频得到.不妨记事故初始时刻为0.由于泊松过程具有独立增量性,故可以分钟为单位时间,记录每隔一分钟进入上游车道的车辆数.由于在城市交通中,大型汽车如公交、卡车等占用道路多、需要的交通资源多,且一旦发生事故,影响较大,因此我们在模型中将大型汽车折算成1.5个小型汽车.据参数估计的替换原理[2],实际计算时我们可以用样本均值代替总体均值λ.设第i分钟进入上游车道的车辆数为ni,则可以令


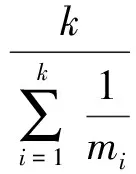

2 交通堵塞程度的预测
下面我们利用上述模型给出交通堵塞车流长度的计算方法.
令X1(t)表示[0,t)内通过事故横断面的车辆数,t为事故持续时间,显然P[X1(0)=0]=1.
记T表示第i辆车与第i+1辆车服务时间间隔,从而有
P[X1(t)=n]=P[X1(t)≥n]-P[X1(t)≥n+1]=
P(T1+T2+…+Tn≤t)-P(T1+T2+…+Tn+1≤t).
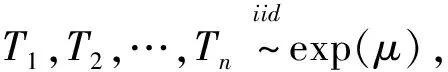
另一方面,由于exp(μ)=Ga(1,μ), 从而利用伽玛分布可加性质有
T1+T2+…+Tn~Ga(n,μ);T1+T2+…+Tn+1~Ga(n+1,μ),
故P[X1(t)=n]=P(T1+T2+…+Tn≤t)-P(T1+T2+…+Tn+1≤t)=
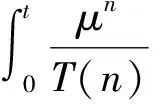
由此可以计算得
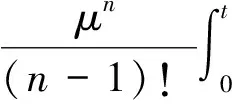
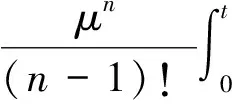
上述计算说明X1(t)服从参数为μt的泊松分布,进一步我们易知EX1(t)=μt.另一方面,若令X(t)表示 [0,t)内到达上游车道的车辆数,根据假设X(t)服从参数为的λt泊松分布,故EX(t)=λt,从而 [0,t)内车道排队等候的车辆数
Y(t)=n0+X(t)-X1(t),
其中n0表示事故发生时上游车道内原有的车辆数,进一步
EY(t)=n0+(λ-μ)t.
其中t为事故持续时间,而λ表示上游车辆进入车道的速率,μ表示离开事故截面的速率,且μ衡量了事故横断面的实际通行能力,而[0,t)内排队等候车辆的数学期望EY(t)反映了排队的长度.
[1] 杨佩昆, 张树升. 交通管理与控制?[M]. 北京:人民交通出版社,1995. 164-168.
[2] 郭冠英, 邹智军. 道路阻塞时的车辆排队长度算法?[J].中国公路学报,1998(3):92-95.
[3] 陈诚, 谭满春. 交通事故影响下事发路段交通流量变化分析?[J]. 科学技术与工程,2011,28(1):4-6.
[4] 孔惠惠,秦超,李新波,等. 交通事故引起的排队长度及消散时间的估算?[J]. 铁道运输与经济, 2005(5):65-67.
[5] 刘次华. 随机过程及其应用?[M]. 北京:高等教育出版社,2004.
[6] 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程?[M]. 北京:高等教育出版社,2004.
ModeloftheEffectofTrafficAccidentsintheCityontheRoadCapacity
HU Hong
(School of Mathematical ScienceHuaiyin, Normal University, Huaian Jiangsu 223001, China)
In this paper, we analyze that the relationships between the traffic congestion and the road capacity, the vehicle flow on the upper section of road, and bulid a mathematical model. Using the model, we can calculate the length of the vehicles in the traffic congestion
poisson process;M/G/1 queuing system; gamma distribution; exponential distribution; parameter estimation
2013-08-25
淮安市科技支撑计划项目(HAS2012078)
胡宏(1967-), 女, 江苏金湖人, 教授, 主要从事组合数学与数论的研究.
O226
A
1671-6876(2013)04-0296-03
[责任编辑李春红]

