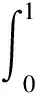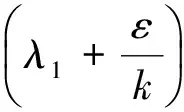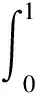二阶时滞微分方程边值问题的正解

蹇玲玲, 赵西君

(青岛理工大学 琴岛学院, 山东 青岛 266106)

二阶时滞微分方程边值问题的正解

蹇玲玲, 赵西君

(青岛理工大学 琴岛学院, 山东 青岛 266106)

利用锥映射不动点指数定理研究了二阶时滞微分方程的边值问题

证明了其正解的存在性.

二阶时滞微分方程; 边值问题; 正解

0 引言

近年来,时滞微分方程的边值问题受了广泛地关注,其中蒋达清等[3]利用锥映射不动点指数定理研究了二阶时滞微分方程边值问题

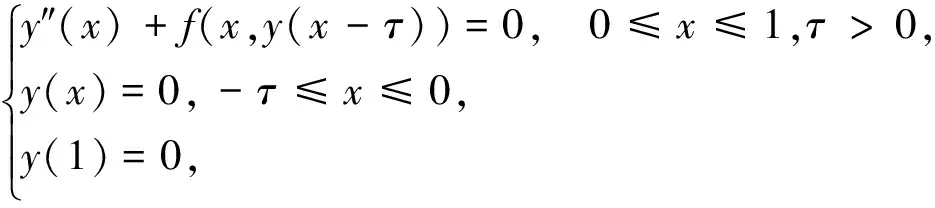
正解的存在性．Jiang[4]利用锥映射不动点指数定理研究了二阶时滞微分方程边值问题

受以上作者的启发,本文考虑二阶时滞微分方程边值问题

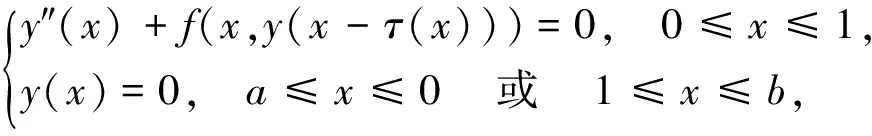
(1)

正解的存在性．其中

(P1)τ(x)是定义在[0,1]上的连续函数,满足

p=inf{τ(x);0≤x≤1},q=sup{τ(x);0≤x≤1},

这里a=min{0,p},b=max{1,q}.

(P2)f(x,y)是定义在[0,1]×[0,+∞)上的非负连续函数．

1 预备知识和引理

首先我们给出BVP(1)的解和正解的定义．

定义如果y(x)满足下面的条件,则称y(x)是BVP(1)的一个解:

1) 在[a,0]和[1,b]上连续非负;

2) 当x∈[a,0]∪[1,b]时,y(x)=0;

3) 当x∈[0,1]时,y″(x)=-f(x,y(x-τ(x)))．

更进一步,如果当x∈[0,1]时,有y(x)>0,则称y(x)是BVP(1)的一个正解．

假设y(x)是BVP(1)的一个解,则

(2)

Green 函数:

显然,当(x,t)∈(0,1)×(0,1)时,0

x(1-x)G(t,t)

(3)

由式(2)和式(3),对BVP(1)的每一个解,y(x)都有

(4)

其中,‖y‖[0,1]:=sup{|y(x)|;0≤x≤1}

令φ1(x)=sinπx是特征方程-φ″=πφ,φ(0)=0,φ(1)=0的第一特征值λ1=π2所对应的特征函数．我们将用到如下的锥映射不动点指数定理:

引理1 设X是Banach空间,K是X中的锥,定义Kp={u∈K,‖u‖≤p},假设Φ:K→K使紧映射,且当u∈∂Kp={u∈K,‖u‖=p}时,有Φu≠u,则

1) 如果当u∈∂Kp时,‖u‖≤‖Φu‖,那么i(Φ,Kp,K)=0;

2) 如果当u∈∂Kp时,‖u‖≥‖Φu‖,那么i(Φ,Kp,K)=1．

定义

X={u∈C[a,b]:当x∈[a,0]∪[1,b]时,u(x)=0}，

令‖u‖:=sup{|u(x)|;a≤x≤b},则X是Banach空间,且当u∈X时,‖u‖=‖u‖[0,1]．

定义X中的锥

K={u∈X;u(x)≥x(1-x)‖u‖,x∈[0,1]}．

定义算子Φ:K→K为

则我们有下述引理.

引理2Φ(K)∈K．

引理3Φ:K→K是全连续的．

2 主要结果及证明

定理1 假设(P1)(P2)成立,则只要下列条件之一成立,则BVP(1)至少存在一个正解y(x)．

推论将定理中的条件(H1)或(H2)改为下列条件(H3)或(H4),定理的结论仍然成立．

(H3) minf0=∞,maxf∞=0;

(H4) minf∞=∞,maxf0=0.

为证明定理,我们再给出以下两个引理．

引理4 设(H3成立,则存在r0,R0:0

i(Φ,Kr,K)=0,0

引理5 设φ1(x)成立,则存在r0,R0:0

i(Φ,Kr,K)=1,0

定理1的证明对0

则Φiu(i=1,2):K→K是全连续算子,由引理4及引理5推出

i(Φ1,Kr,K)=0,0

及i(Φ2,Kr,K)=1,0

定义Hi(s,u)=(1-s)Φu+sΦiu(i=1,2),则对∀s∈[0,1],Hi是全连续算子,另一方面,对∀ω>0和i=1,2,当s1,s2∈[0,1],u∈Kω时,总有

|Hi(s1,u)-Hi(s2,u)|≤|s1-s2|[‖Φiu‖+‖Φu‖,]

而在Kω上‖Φiu‖+‖Φu‖一致有界．因此,Hi(s,u)当s∈[0,1]时,对u∈Kω一致连续,由文[1]可知,在[0,1]×Kω中,Hi(s,u)是全连续算子．

假设(H1)成立,由(H1)的第一个不等式和f1的定义,∃ε>0和r1:0

(5)

下面证明:对u∈∂Kr1和s∈[0,1],有H1(s,u)≠u．用反证法,假设存在s1:0≤s1≤1和u1∈∂Kr1,使得H1(s1,u1),则u1(x)满足

(6)

u1(x)=0,a≤x≤0 或 1≤x≤b

(7)

把式(6)两边同时乘以φ1(x),再从0到1积分,利用两次分部积分法和式(7)得

0

(8)

由式(5)和(H2)得

矛盾．

所以对u∈∂Kr1和s∈[0,1],有H1(s,u)≠u．有度的同伦不变性[1,2],

i(Φ,Kr1,K)=i(H1(0,·),Kr1,K)=i(H1(1,·),Kr1,K)=i(Φ1,Kr1,K)=0

(9)

另一方面,由(H1)的第二个不等式, 存在ε>0和R′>R0,使得

下证∃R1≥R′使得

H1(s,u)≠u, ∀s∈[0,1],u∈K,‖u‖≥R1

(10)

反证法,如果∃s1∈[0,1],u1∈K使得H1(s1,u1)=u1,则有

i(Φ,KR1,K)=i(Φ1,KR1,K)=1

(11)

由式(9)和式(11),得i(Φ,KR1Kr1,K)=1,则Φ在KR1Kr1有不动点．

同理可证当(H2)成立时,结论也成立．假设y是Φ在KR1Kr1中的不动点,因为0

[1] Li Z Y,Ye Q X. Tgeory of reaction-duffusive equations?[M]. Beijing: Scientific Press, 1990.

[2] Guo D J. Nonlinear functional analysis?[M]. Jinan: Shandong Scientific Press, 1985.

[3] 蒋达清, 张丽莉. 二阶时滞微分方程边值问题的正解?[J]. 数学学报, 2003, 46: 739-746.

[4] Jiang D Q. Multiple positive solutions for boundary value problems of second-order delay differential equations?[J]. Appl Math Lett, 2002, 15: 575-583.

[5] Bai D Y, Xu Y T. Existence of positive solutions for boundary-value problems of second-order delay differential equations?[J]. Appl Math Lett, 2005,18: 621-630.

PositiveSolutionsforBoundaryValueProblemsofSecond-OrderDelayDifferentialEquations

JIAN Ling-ling, ZHAO Xi-jun

(Qindao College, Qingdao Technological University, Qingdao Shandong 266106, China)

We use a fixed point index theorem in cones to study the existence of positive solutions for boundary value problems of the second-order delay differential equations

second-order delay differential equations； boundary value problems； positive solutions

2013-07-12

蹇玲玲(1983-), 女, 山东临沂人, 讲师, 硕士, 研究方向为微分方程及其应用.

O175.8

A

1671-6876(2013)04-0283-04

[责任编辑李春红]