与Hermite算子相关的算子有界性

曹勇辉，周 疆

（新疆大学 数学与系统科学学院，新疆 乌鲁木齐830046）

在经典分析中，拉普拉斯算子是一个很重要的算子，许多文献对它做过各种讨论，其中在微分方程中用得较多的是它的幂算子与乘子算子在各种函数空间上的有界性，它对应着解的估计．因为Hermite函数系构成了函数空间L2（Rn）上的一组完备正交基，所以Hermite函数展开问题的研究颇受重视，注意到Hermite函数是Hermite算子的特征函数，故对Hermite算子的研究很有意义．与Hermite算子相关的乘子算子与幂算子在一些经典空间中的有界性已经有很多作者研究［1－3］，本文讨论这些算子在与Hermite函数相关的Triebel－Lizoekin空间中的有界性．

1 基本概念

设D是一个自伴正的算子，作用在L2（Rn），那么有Df＝其中dE为算子D的谱解集．对α∈R，0＜p，q＜ ∞，取φ∈Φ，其中Φ＝｛φ∈C∞：suppφ⊂［1／2，2］，｜φ（λ）｜＞c＞0，λ∈［3／4，7／4］｝，文献［1］引入了与算子D相关的Triebel空间．

定义1［1］与算子D相关的Triebel空间定义为其中

如果算子D为拉普拉斯算子，那么此函数空间就是经典的Triebel－Lizorkin空间［2，4］；如果D＝H，H＝－Δ＋｜x｜2是Hermite算子，文献［5］得到H0，2p＝Lp，p＞1．

下面给出乘子算子与幂算子的定义．

定义2［6］函数m：R＋→C被称作Hα，qp上的乘子，如果算子m（H）：L2→L2能有界延拓到Hα，qp．

引理1［6］α∈R，1＜p＜ ∞，如果有界函数m：R＋→C满足｜m′（t）｜≤ct－1，那么乘子m在空间上有界．

注意引理1只是在一维空间上成立，本文利用乘子算子的加权有界性把这个结果推广到高维空间仍然成立．

利用Hermite半群表示，可以定义Hermite算子的虚幂算子．

定义3［7］．它的积分表示的积分核为

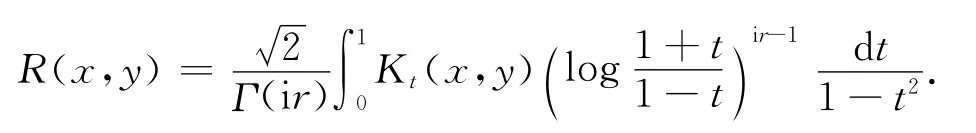
其中Ks（x，y）＝

对此算子，文献［8］得到它的加权有界性，类似的对拉普拉斯算子的虚幂算子的结论在文献［8－9］中已经研究．

引理2［7］如果1＜p＜ ∞，w∈Ap，那么有H－ir在Lp（w）上有界．

本文考虑上述算子在Hα，qp空间中的有界性．证明过程中出现的常数c不依赖于主要指标，它在不同的地方出现其值可以不一样．

2 结论及证明

首先证明下面的引理．

引理3 Ha，qp的对偶空间是H－a，q′p′，其中a∈R，1＜p，q＜ ∞，1／p＋1／p′＝1，q／1＋1／q′＝1．

证明 取f（x）∈H－a，q′p′，φ∈Φ满足∑φ2k（x）＝1，x≠0，那么其中Qkf＝有

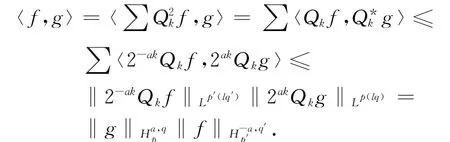
取f∈Ha，qp，因为f→ ｛2kaQkf｝为从Ha，qp到Lp（lq）子空间的一一映射．每个函数g∈（Ha，qp）′可以看成子空间上的泛函，应用延拓定理，g为Lp（lq）上连续泛函，利用（Lp（lq））＝Lp′（lq′），若φ为Schwartz函数，得到g（φ）＝∫∑gk（x）Qk（x）dx，‖2－kagk‖Lp′（lq′）～‖g‖．

引理4 线性算子T满足TH＝HT和‖Tf‖Lq（w）≤c‖f‖Lq（w），‖Tf‖Lq′（w）≤c‖f‖Lq′（w），其中1＜q＜∞，w∈A1．那么当a∈R，1＜p＜∞时，T是从Ha，qp到Ha，qp有界的．

证明 取φ∈Φ，∑φ2k（x）＝1，x≠0，其中φk（x）＝φ（2－kx）．那么取g∈H－a，q′p′，

〈Tf，g〉＝∑〈TQkf，Qkg〉≤ ∑〈2akTQkf，

定义如下g函数［3］：

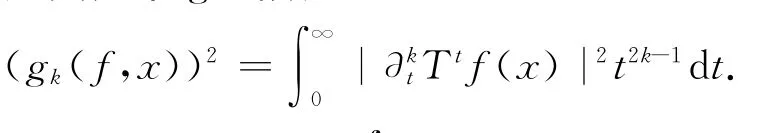
其中Ttf（x）＝（2π）－n／2∫Kt（x，y）f（y）dy，Kt（x，y）＝ （2πsinh 2t）－n／2exp（－1／2｜x－y｜2coth 2txytanh t）．

引理5［3］对每个k≥1与f∈L2，有‖gk（f）‖22＝2－2kΓ（2k）‖f‖22．

引理6［3］核Kt（x，y）的估计满足

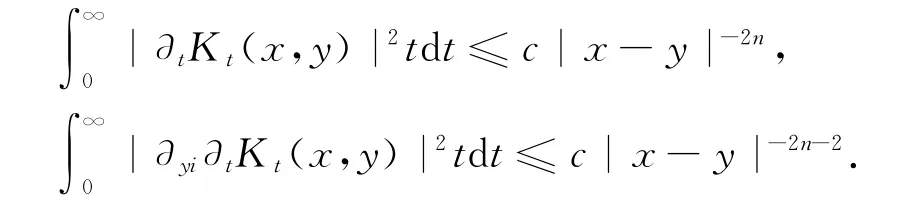
应用这两个引理可以证明

引理7 如果w∈Ap，1＜p＜ ∞，那么‖g（f）‖Lp（w）与 ‖f‖Lp（w）等价．

证明 取E＝L2（R＋，tdt），Tf（x）＝∫∂tKt（x，y）f（y）dy，则有

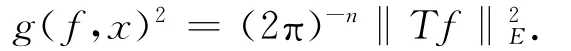
利用向量值奇异积分理论有g在Lp（w）上有界．

极化 ‖g（f）‖22＝2－1‖f‖22得到

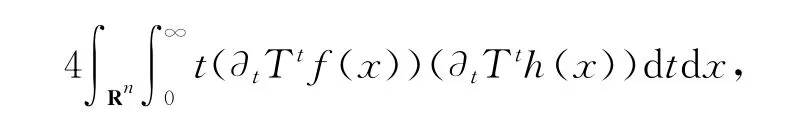
取h1（x）＝w（x）1／ph（x），得到

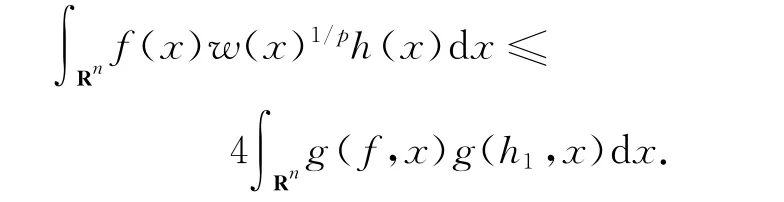
应用Hölder不等式有

其中1／p＋1／q＝1，但是‖g（h1）‖Lq（w）≤c‖h1‖Lq（w）＝c‖h‖Lq．得到

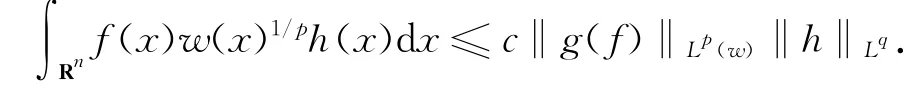
通过对h（x）取上确界有‖g（f）‖Lp（w）≥c‖f（x）‖Lp（w）．完成引理7的证明．

对k≥1，引进

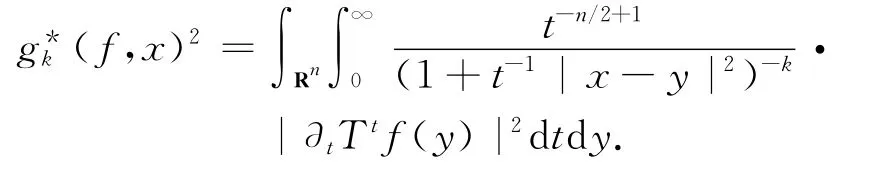
引理8 如果p≥2，k＞n／2，w∈Ap／2，那么g＊k在Lp（w）上有界．

证明 因为k＞n／2，故

即有∫Rn（g＊k（f，x））2h（x）dx≤

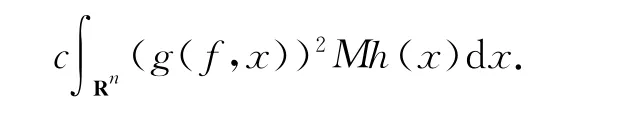
取h1（x）＝w（x）2／ph（x），利用极大函数的加权结果可以得到

对h取上确界，即可完成引理8的证明．

下面证明乘子的有界性．

定理1 取α∈R，1＜p＜∞，如果m：R＋→C为有界的并且满足｜m′（t）｜≤ct－1，那么m在Ha，qp（Rn）上有界．

证明 注意到g（m（H）f（x），x）≤ckg＊k（f，x）［3］与gk（f，x）≤cgk＋1（f，x），利用引理7和引理8即有

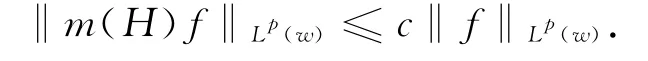
其中p≥2，当1＜p＜2，对偶操作可以得到类似结果，即乘子是加权有界的，应用引理4即可完成证明．

定理2 取1＜p，q＜ ∞，a∈R，H－ir（r≠0）是从Ha，qp到Ha，qp有界的．

证明 应用引理2与引理4，可以得到证明．如果幂为实的，那么有

证明 由于f＝H－rHrf，

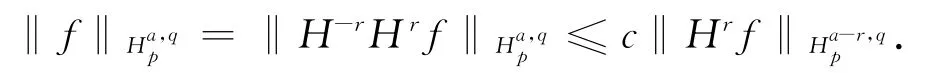
令φ（x）∈Φ，ψ（x）＝xrφ（x），那么ψ∈Φ．记ψk（x） ＝ ψ（2－kx），ψk（H） ＝ ψ（2－kH） ＝2－krHrφ（2－kH），则有

综上完成定理3的证明．

3 结语

利用算子的加权有界性与对偶方法，证明了与Hermite算子可交换的算子在Triebel－Lizorkin空间中的有界性，并得到乘子算子与幂算子在Triebel－Lizorkin空间中是有界的．由于算子在各种空间的有界性可以反映出一些相关的微分方程解的信息，所以此类算子在理论研究和应用中都有很大作用．

［1］Jacek Dziubanski．Triebel－Lizorkin spaces associated with Laguerreand Hermite expansions［J］．Proceedings of the American Mathematical Society，1997，125：3547－3554．

［2］Triebel H．Theory of function spaces［M］．Basel：Birkhαuser Verlag，1983．

［3］Thangavelu S．Lectures on Hermite and Laguerre expansions［M］．Princeton：Princeton University Press，1993：5－9，85，86，87，90－91．

［4］Triebel H．Theory of function spacesⅡ［M］．Basel：Birkhαuser Verlag，1992：16－19．

［5］Epperson J．Triebel－Lizorkin spaces for Hermite expansion［J］．Studia Mathematica，1995，114：87－103．

［6］Jay Epperson．Hermite multipliers and Pseudomultipliers［J］．Proceedings of the American Mathematical Society，1996，124（7）：2061－2068．

［7］Krzysztof Stempak，JoséLuis Torrea．Higher Riesz transforms and imaginary powers associated to the harmonic oscillator［J］．Acta Mathematica Hungarica，2006，111（1／2）：43－64．

［8］Adam Sikora，James Wright．Imaginary powers of Laplace operators［J］．Proceedings of the American Mathematical Society，2001，129（6）：1745－1754．

［9］Zorko Cristinat．The Morrey space［J］．Proceedings of the American Mathematical Society，1986，98：586－592．