大跨径钢箱梁在温度影响下的振型分析

刘钦振

(天津市海河建设发展投资有限公司，天津 300380)

桥梁结构的自振特性对正确进行桥梁的抗震设计、健康检测和维护具有十分重要的意义.其中，桥梁的自振频率与主振型是进行结构动力分析和抗震设计的重要参数，也是使用阶段判别桥梁是否存在损伤的基本依据.在桥梁鉴定和验收规范中，对桥梁的竖向和横向自振频率的限值均有一定的规定.由于钢材导热性能好，对温度变化比较敏感，在日照条件下会使桥梁内部产生较大的温差，致使产生较大的温度应力，从而影响桥梁的振动特性，对桥梁的正常使用带来安全隐患.因此，对温度作用下大跨径连续钢箱梁桥的自振特性进行研究分析是很有必要的.笔者以某连续变截面钢箱梁桥为例，研究其在温度荷载作用下的全桥振动情况，可为桥梁的设计施工提供参考.

1 振型分析方法

1.1 振动微分方程

桥梁结构的振动特性主要取决于它的各阶自振频率和主振型等，动力分析的运动微分方程为

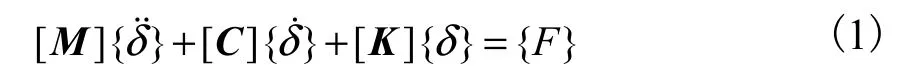
式中：[M]、[C]、[K] 分别为桥梁结构的质量、阻尼、刚度矩阵；δ˙˙、δ˙和δ分别为桥梁结构的加速度、速度和位移向量；F为作用于桥梁空间梁单元的力向量.求桥梁的自振特性时，一般不考虑阻尼的影响，令[C]＝0、{F}＝0，则得到其无阻尼自由振动的微分方程为[1]

式(2)具有非零解的条件为

1.2 特征方程的求解方法

对于式(3)求解广义特征值问题的方法比较多，常用的有向量迭代法、逆迭代法、Jacobi(雅可比)法子、空间迭代法等.往往不一定要求解所有的振型和频率，也没必要求出所有的特征值，只需按要求求出较低的几阶，这样既能节省存储振型所用的空间，又可大大节省计算的时间.本文采用子空间迭代法来求解特征方程.

子空间迭代法是目前求解大型结构自振频率和振型的最有效的方法之一，已经广泛应用于大型结构动力学的有限元分析中.子空间迭代法主要利用了质量和刚度矩阵的带状特性，为精确地求得一个体系的p个振型和频率，首先可取q个试探向量(q＞p)，位移可以表示为如式(4)的多个形状的组合

对于 p个特征值和特征向量的广义特征值方程可写成

式中：矩阵Φ 中的各列代表所要计算的特征向量，Λ是一个对角线元素为特征值的对角矩阵，即

在方程(5)右边代入 q 个试探向量，得

求解式(8)得到未规格化的改进的形状，即

式(9)改进的形状用于下一轮新的迭代之前，它们必须用规格化和正交化修正.规格化使其在计算中数值大小保持合理，正交化使得每一个向量收敛于不同振型(而不是全部收敛于最低振型).这些运算能按多种不同的方式来实现，但是最方便而且两者立即就可以完成的方法是进行一次Ritz特征问题的分析.第一次循环的广义坐标刚度和质量矩阵，计算如下

求解对应的特征问题，即

2 有限元模型的建立

2.1 工程背景

以某连续变截面钢箱梁桥为例，该桥主桥采用57.5 m＋85 m＋57.5 m三跨跨越海河，计算简图如图1所示.主桥横截面由7个钢箱梁组成，每个钢箱梁宽度为 3.452 m，钢箱梁之间间距为 1.644 m，顶板、底板和腹板厚度分别为 20 mm、20 mm和14 mm.钢箱梁顶面与道路纵断线形一致，底面为曲线线形.两个钢箱梁之间采用上下两个横梁进行连接.钢箱梁内部设有大横隔板和小横隔板，大、小横隔板的标准间距分别为5 m和2.5 m，钢箱梁之间横梁布置位置对应大、小横隔板.

图1 钢箱梁计算简图

2.2 ANSYS模型

采用有限元分析软件ANSYS建立连续变截面钢箱梁的有限元模型.根据钢箱梁的薄壁特点，钢箱梁采用壳单元shell63模拟[2]，模型节点为4324个，单元为23690个.ANSYS模型采用1∶1比例建立，主要分析该桥的主梁段——钢箱梁在温度荷载作用下其振型的变化情况，ANSYS计算模型如图2所示.

在建模过程中，由于要考虑温度荷载的影响，根据《公路桥涵设计通用规范》(JTG D60—2004)，最高有效温度为39 ℃、最低有效温度为-15 ℃；温度梯度按《公路桥涵设计通用规范》(JTG D60—2004)规定选用.由于全桥主要采用焊接连接，施工时间是在白天，故可考虑最高有效温度取 39 ℃，最低有效温度取 15 ℃，施加在钢箱梁上的最大温差可取为24 ℃.此外，对于钢箱梁模型的边界条件[3-4]，考虑全桥成型之后的边界约束，即在钢箱梁的两端施加X，Y，Z三个方向的全约束，在中间两个中墩处只加竖向即Y方向的约束.

图2 ANSYS计算模型

由于此钢箱梁桥比较复杂，所以在建模中做了一定的简化处理.例如，增加桥梁竖向刚度的加劲肋在建模过程中就不在出现，而是增加箱的厚度来实现.还有连接各箱梁之间的箱间横隔板，用矩形板代替实际桥梁的工字型板.这样处理的目的和结果是使建出来的桥梁模型在不影响整体结果的情况下，使计算过程相对便捷.

3 计算结果与分析

3.1 模型计算结果

在有限元模型上考虑温度和自重荷载[5]，对有限元模型设置边界条件，采用Block-Lanczos 法提取前l0阶模态.模态分析所得的阵型的大小是对应的固有频率下振动的相对量值，并不反映真实值.经过多次对钢箱梁施加荷载进行计算分析，最后综合比较得出本桥在温度荷载作用下的前 6阶模态竖向位移如图3(a)-(f)所示.为了分析温度对桥梁的振型的影响，又做了桥梁仅在自重作用下的模态分析，观察其振动频率的变化，对比结果列于表1中.

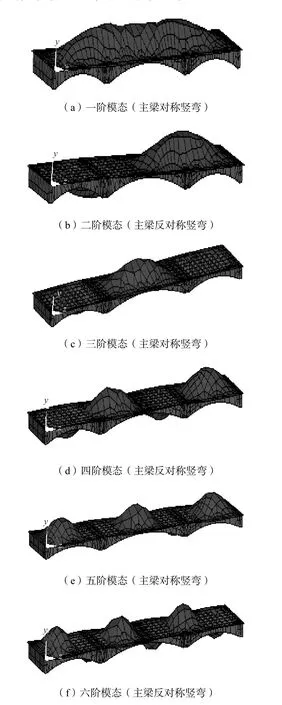
图3 前6阶模态竖向位移

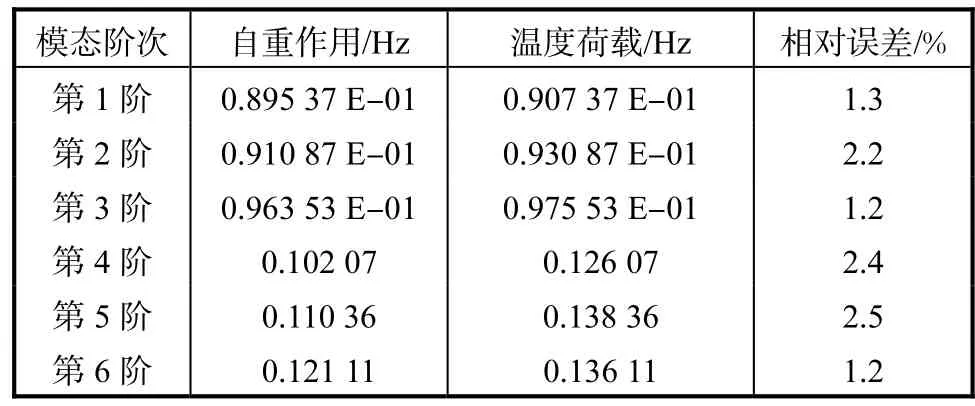
表1 钢箱梁在自重与温度荷载下的模态频率对比

3.2 结果分析

由以上结果可得出以下几点结论.

(1)从图3中可以发现，钢箱梁的前6阶模态变形图均出现了主梁的竖向阵型，即主梁竖桥向弯曲，主梁竖向弯曲的阵型最早出现，三跨主跨的跨中挠度最大，全桥的最大振幅均出现在梁的跨中位置.其一阶模态变形图为整桥沿向上竖向弯曲变形，二阶为中跨向上竖弯，两边跨向下竖弯，三阶为反对称竖向弯曲变形，而第4，5，6阶模态变形与前三阶变形相比，就显得复杂.例如第4阶，仍旧是主梁段的反对称竖向弯曲，若取主梁的一半来看，仍旧是反对称竖弯，这说明箱梁的振动比前面几阶要来得剧烈.而且，从各阶变形图中可以发现，就整个钢箱梁桥来说，跨中为其薄弱的部分，厚度小，导致刚度也比其他部位小，在施工过程中尤其值得关注，应尽量避开温度作用影响比较大的时段，如在温度相对比较低的天气进行合拢段施工.

(2)结合图3和表1可以看出，无论是否施加温度荷载，钢箱梁的前六阶阵型基本不变，只有频率有一定的变化.主要振动形式为主梁的竖向弯曲振动，基本上没有箱梁的横向振动，这说明桥梁的横向刚度足够大，虽然主梁由七片小箱梁组成，但是箱间有大小横隔板连接及加劲肋支撑，增加了其横向刚度及整体受力性能，也进一步说明桥梁设计的横向刚度是符合要求的.

(3)由表1中数据比较可得，模态振动频率在施加温度荷载下有一定的变化.温度荷载作用下钢箱梁桥的振动频率随着温度的升高而呈现上升的趋势.而且，前三阶模态频率与第4，5，6阶模态频率相比，原有数值与相对误差都比较小，最大误差为 2.5%，基本上都在 2%左右[6]，说明钢箱梁在前三阶的振动情况不如后面剧烈.而导致模态频率变化的因素可能是结构模型施加的边界条件，模型的几何尺寸，及结构的受力状况等受到温度作用的影响发生了变化.笔者在建模计算过程中运用的是相同的模型，故几何尺寸的影响可以忽略不计，而两次计算中边界条件的设置也是相同的，因此可以推断，在温度荷载作用下，其模态频率的变化应该是由于桥梁结构内部的受力情况发生重分布引起的.因为，钢材的线性膨胀系数比其他材料大，对温度变化也比较敏感，当其外部温度分布不均匀时，由于热胀冷缩的效应，钢箱梁会发生局部膨胀或局部收缩，膨胀处产生拉应力，收缩处产生压应力[7]，从而使箱梁的内部应力重新分布，进而对其模态频率产生影响.

4 结 论

(1)通过以上的建模与计算，从中可以发现，在ANSYS中用shell63单元进行薄壁钢箱梁桥的模拟分析是可行的，而且，在具体的实践中发现，特别是对于一些薄壁结构，在不影响结果的前提下，就shell63单元与solid单元相比较，前者要便捷简单一些，特别是模型建成之后的加载运算，远远比后者要小，不但可以节省计算时间，也更容易输出结果.

(2)从得出的结果中可以发现，薄壁钢箱梁的刚度在其三个跨中截面相对较小，属于薄弱截面，在模态分析中，变形也最大，再加上温度荷载的影响，这些梁端的受力会更加复杂.变形可能也会发生一些不可预料的变化，在施工监测或是监控中是尤其需要考虑的，应加大施工中对三跨主跨跨中截面监测或监控的力度.

(3)笔者使用有限元软件ANSYS进行模拟分析，所得结果与实际情况基本符合，故可知本文所应用的基本理论和有限元分析方法是成熟、可信的，其计算结果可为本桥动力作用分析提供参考.另外，采用的有限元模态分析仅限于线弹性分析，对于非线性动力分析，还有待进一步研究探讨.

［1］贾艳敏，王佳伟，韩基刚. 预应力简支钢箱梁固有频率影响因素分析[J]. 工程力学，2009，26(6)：37-40.

［2］李枝军，李爱群，韩晓林. 润扬大桥悬索桥动力特性分析与实测变异性研究[J]. 土木工程学报，2010，43(4)：92-98.

［3］屈爱平，高淑英. 梁-墩-桩基的动力特性研究[J]. 西南交通大学学报，2001，36(6)：641-644.

［4］孙正华，李兆霞. 润扬斜拉桥有限元模拟及模态分析[J]. 地震工程与工程振动，2006，26(2)：25-32.

［5］彭大文，陈昀明. 钢筋混凝土加劲析架悬索桥的模态分析[J]. 地震工程与工程振动，2001，21(4)：40-45.

［6］徐 良，江见鲸，过 静. 广州虎门悬索桥的模态分析[J]. 土木工程学报，2002，35(1)：25-34.

［7］项海帆. 高等桥梁结构理论[M]. 北京：人民交通出版社，2002.