具有无标度特性的港口网络演化模型

王 丹，李蓓蕾

（沈阳大学 装备制造综合自动化重点实验室，辽宁 沈阳 110044）

自从2001年加入WTO以来，中国的对外贸易总额日益增加，已有的统计数据显示，2002—2007年，我国的对外贸易总额占国内生产总值的60%以上［1］.这说明对外贸易已经成为国内经济发展不可或缺的一部分.海洋运输是对外贸易最主要的交通运输方式之一.据中华航运网预测报告显示，国际贸易总运量中的2／3以上、中国进出口货运总量的约90%都是利用海上运输［2］.由此可见，海洋运输对国民经济的可持续发展起着至关重要的作用.

海洋运输又称“国际海洋货物运输”，是国际物流中最主要的运输方式.它是指使用船舶通过海上航道在不同国家和地区的港口之间运送货物的一种方式.可以把海洋运输系统看做由数百个港口和数以万计的船舶组成的，随时间演化的复杂系统［3］.

复杂网络是研究复杂系统的一门新兴学科，可以把复杂系统抽象成由许多个相互连接的节点组成的复杂网络，如人际关系网络、万维网、因特网、交通网、生物网、E-mail网络、科学合作网，等等.各个学科的学者们对复杂网络的各个层面进行了深入研究，提出了规则网络、随机网络［4］、小世界网络［5］、无标度网络［6］等复杂网络演化模型.

将各地的港口确定为港口网络中的单个节点，如两个港口之间有船舶进行货物运输，则确定它们之间有一条边，这样就把整个海洋运输系统抽象为一种复杂网络的图，这种拓扑图可以让人们从整体的角度来对海洋运输系统中不同地区，不同功能的港口之间复杂的航运运输关系进行模拟和分析［7-8］.也可以通过这种拓扑图了解海洋运输系统的结构特征，找出这种结构的演化机理及其中存在的潜在规律.基于以上考虑，提出一个能够有效再现实际港口网络系统的一些统计特性的随时空演化的加权港口网络模型.

1 港口网络演化模型

很多现实网络都可以用复杂网络来描述，但目前采用最多的是无权网络，无权网络没有考虑节点之间连接的强度.但现实的许多网络中，节点之间的相互作用强度存在着显著的差异.例如，在航空网络中，不同型号飞机运载旅客数量的差异；在城市交通网络中，城市的主干道在交通网络里的重要性要远大于一般的三四级公路；在因特网中，路由器之间传输能力的差别；海洋运输网络中，两个港口之间通航的船舶的数量［9-14］.此时就需要通过加权网络边之间不同的权值来表示这种强度的差异.当今，已有越来越多的学者开始研究加权网络模型，其中应用最广泛的为BBV模型［15］.随着模型规模的增大，BBV模型网络的度、权值和强度都呈现无标度特性.但现实的航运网络中，除了以上特性外，因为相邻港口之间连接的紧密性，港口网络还具有高聚类的特点.因此，本文所提出的港口网络演化模型不仅考虑了新加入的港口和已有港口间建立连接，还考虑了新的航线可以建立在已有港口之间，应用此规则可以明显增大网络的聚类系数.

本文的建模思想基于HK模型［16］，将三角连接机制引入BBV模型中［17］，通过控制参数α调节新旧港口之间的连接强度，构建出一个具有高聚类系数的加权无标度港口网络演化模型.模型生成过程如下：

第1步 以m0个完全相连的节点（港口）作为初始态.边（两个港口之间有船舶往来）的初始权值设定为w0＝1.

第2步 以概率p（p∈ ［0，1］），增加一个新节点（港口）v.该节点带有m（m≤m0）条边，连接节点的概率如下：

式中，wij是港口网络中节点间边权值，表示节点（港口）i和节点（港口）j之间货运的吞吐量，研究表明在更广的范围内港口之间的货运量比较平衡，可以表示为wij＝wji，认为港口网络为无向网络.si是港口网络中节点i的强度，表示港口i与其相邻港口之间的货物运输总数量.

式（1）中α是可控制参数，当α较大时，说明强度大的港口更易与新港口进行连接，也就是说新建的港口更容易与大型港口相连接；当α较小时，网络中节点（港口）与新节点（港口）连接的概率就会相接近，也就是说新建的港口不仅与大型港口相连接，也会考虑其他因素与其他小型港口相连接.

在港口网络中新旧港口之间建立连接势必会造成其他港口间货运关系的变化，这种变化按照式（2）的规则进行：

式中，Δwij是节点i和节点j之间边权的增量，这里不考虑新节点v和节点i的邻居的邻居节点相连所引起的节点i的强度的变化.值得注意的是，此处增量δ具有明显的物理含义，当δ＝w0时，表示老港口i倾向于中转港口，新港口v与老港口i之间的货运完全被与老港口i相连的其他港口所分担；而当δ＝0时，表示与老港口i相邻的港口均没有起到分担作用；当δ＜w0时，表示老港口i留下了某些从新港口v获取的资源；当δ＞w0时，表示老港口i与新港口v之间有货运关系，并且能取得一些稀有货源，因而使港口i的相邻港口与港口i的关系越发密切.

第3步：以概率1-p，仅增加n条新边.加入新边的两个端点以三角机制连接.首先，随机选取一个边（i，j），再选取节点j的另外一个邻居节点k（排除节点i）.k的选取以概率进行：

如节点i和k之间存在连接，则权值增加σ；如不存在连接，则建立新边.在两种情况下，边wij，wjk的权值都增加σ，其中，σ＝1.

重复以上3步，经过N步后，即将生成网络规模为m0＋Np个节点的加权无标度港口演化模型.

2 网络统计特性分析

在现实生活中，许多网络中的度和强度等基本属性都服从幂律分布.度和强度的统计性质被认为是描述加权网络最重要的统计性质［18-21］.下面通过MATLAB数值仿真分析本文所构造模型的一些基本特性.在仿真中，选取网络规模N＝1 000，m0＝4，m＝3，n＝2，δ＝1，σ＝1，α＝0.9.这里只研究不同参数p对所提加权网络拓扑结构特性的影响.当α＝1，p＝1时，网络模型退化为个BBV模型.

从图1和图2可以看出三角结构机制对港口网络的度和强度分布有着重要的作用.无论参数p为何值，网络的度分布和强度分布均服从幂律分布，即P（k）～k-γk，P（s）～s-γs，且幂律指数γ在1～3之间.在图1中，当p＝1时，γk≈3网络模型退化为BBV模型，BBV模型中的度分布幂律指数γk只在3左右，这种分布特性不符合很多真实网络的结构特点，而当p＝0.3，0.6，0.9时，γk在2～3之间比较符合真实网络的结构特点，这说明本文所提出的加权网络模型符合现实网络的特性，可以模拟现实中的加权网络.

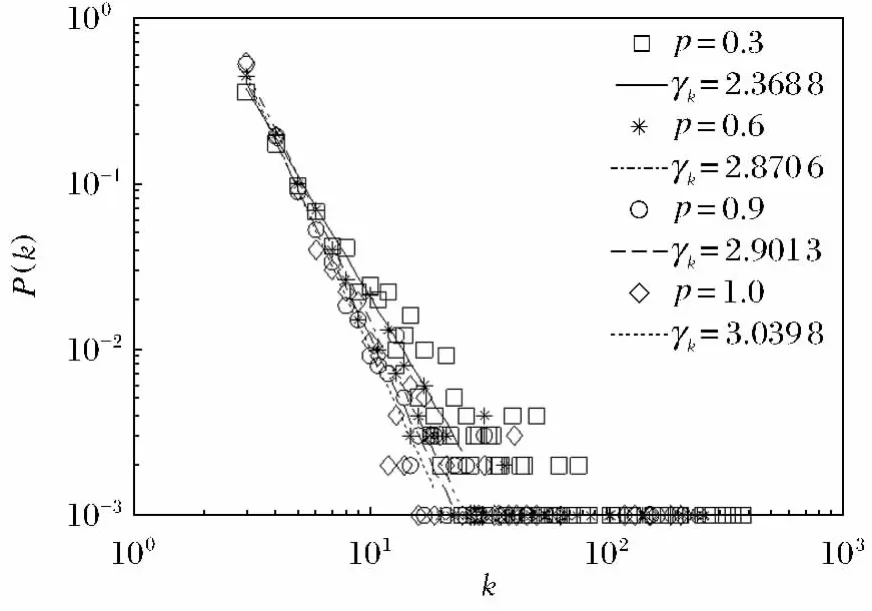
图1 强度分布P（k）随参数p变化曲线Fig.1 The degree distribution P（k）for different values of p

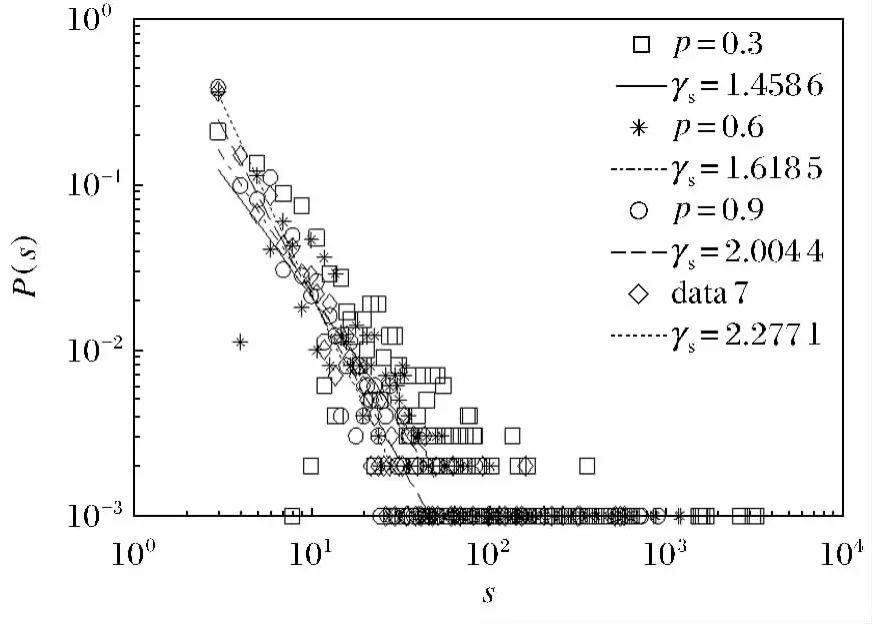
图2 强度分布P（s）随参数p变化曲线Fig.2 The strength distribution P（s）for different values of p

按照中华航运网公布的数据，图3给出了中国港口网络的港口强度和度的分布曲线，从图3的结果可以看出，本文所提出的港口加权网络模型基本符合我国港口网络模型的结构特征.

以前学者所提出的加权网络模型（如BBV模型）虽然具有小的平均最短路径，但它的聚类系数也较小，这种属性并不符合现实网络的拓扑结构特点［16］.

节点i的局部聚类系数Ci可定义为

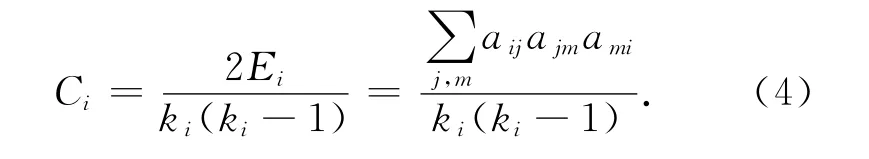
式中，Ei为ki个邻居节点之间实际存在的边数，ki（ki-1）／2为最多可能存在的边数.

整个网络的平均聚类系数C可用所有节点i的聚类系数Ci的平均值表示：

式中，0≤Ci≤1，0≤C≤1，N 为网络中的总的节点个数.

图3 中国港口网络的港口强度分布P（s）和度分布曲线p（k）Fig.3 The strength distribution P（s）and the degree distribution P（k）

图4 C（k）与度的关系随参数p变化曲线Fig.4 The average clustering coefficient distribution C（k）for different p

图4给出了平均聚类系数C（k）与度的关系随参数p变化的曲线.当p值较小时，三角结构占的比重较大，C也较大.从图4可看出，当p＝0.9时，C＝0.154 8；p＝0.6时，C＝0.343 8；p＝0.3时，C＝0.481 2.从图4中还可以看到，C（k）服从网络节点度的幂律分布，即C（k）～k-γC.许多大规模网络都具有明显的聚类效应，例如文献［22］中就计算出一个具有269 504个节点及1 497 135条边的 WWW的聚类系数约为0.29，而一个具有10 697个节点及31 992条边的Interent的聚类系数约为0.39.因此本文所提出的网络演化生产模型不仅可以用在港口网络上还可以应用与其他高聚类系数加权网络的建模研究，如万维网、因特网等高聚类系数的加权网络.

3 结 论

本文利用复杂网络方法对港口网络随时间演化问题以及港口网络本身的结构属性进行了研究，根据现实港口网络中各港口码头连接强弱的非均衡性，提出了一种具有无标度特性的加权港口网络模型.在经典BBV模型的基础上，引入一个控制参数，用以调节新港口与已建港口之间的连接概率.港口网络规模的扩大和港口网络结构的演化是为了适应信息需求的增加，从而使港口网络能够保持运输的高效率.虽然本文所提出的港口网络模型可以初步反映港口网络结构特性，具有高可调聚类系数及度和强度符合幂率属性等特点，但是还不能说明模型与实际的港口网络模型所有属性完全相符，只能说明本文所提的模型在网络的主要属性上可以反映出真实港口网络的一些共同属性，关于这一方面的探讨还有待进一步研究.

［1］ 中华人民共和国国家统计局.2007年国民经济和社会发展统计公报［R］.北京：中华人民共和国国家统计局，2008.（National Bureau of Statistics of China.National Economic and Social Development Statistics Bulletin of 2007［R］.Beijing：National Bureau of Statistics of China，2008.

［2］ 中研普华公司.2009—2012年海运行业发展前景分析及投资风险预测报告［R］.2008.（Zero Power Intelligence. Report ofDevelopment Prospects and Investment Risk Prediction in Maritime Industry 2009-2012［R］.2008.）

［3］ 熊文海.世界航运网络的结构特性及其动力学行为研究［D］.青岛：青岛大学，2009.（Xiong Wenhai.Structural Characteristics of World Shipping Network and its Dynamic Behavior ［D］.Qingdao：Qingdao University，2009.）

［4］ Erdös P，Rényi A.On Random Graphs［J］.Publicationes Mathematicae，1959，6：290-297.

［5］ Watts D，Strogatz S.Collective Dynamics of Small-world Networks［J］.Nature，1998，393（6684）：440-442.

［6］ Barabási A L，Albert R.Emergence of Scaling in Random Networks［J］.Science，1999，286（5439）：509-512.

［7］ 熊文海，张嗣瀛，方爱丽.加权演化的港口网络模型的研究［J］.数学的实践与认识，2008，38（2）：64-69.（Xiong Wenhai，Zhang Siying，Fang Aili.Study on Weighted Evolving Model of Port Network ［J］.Mathematics in Practice and Theory，2008，38（2）：64-69.）

［8］ 张嗣瀛.复杂性科学，整体规律与定性研究［J］.复杂系统与复杂性科学，2005，2（1）：71-83.（Zhang Siying.Complexity Science，Rules of the Whole Systems and the Qualitative Researches［J］.Complex Systems and Complexity Science，2005，2（1）：71-83.）

［9］ 王丹，李彦平，郝彬彬.基于随机交叉机制的同步优化网络模型［J］.沈阳大学学报：自然科学版，2012，24（3）：43-46.（Wang Dan，Li Yanping，Hao Binbin.Synchronizationoptimal Network Model based on Random Interchanging Mechanism［J］.Journal of Shenyang University：Nature Science，2012，24（3）：43-46.）

［10］ Zheng D F，Trimper S，Zheng B，et，al.Weighted Scalefree Networks with Stochastic Weight Assignments［J］.Physical Review E，2003，67（4）：040102.

［11］ Pan Z F，Li X，Wang X F.GeneralizedLocal-world Models for Weighted Networks［J］.Physical Review E，2006，73（5）：056109.

［12］ Ou Q，Jin Y D，Zhou T，et al.Power-law Strength-degree Correlation from Resource-allocation Dynamics on Weighted Networks［J］.Physical Review E，2007，75（2）：021102.

［13］ Wang W X，Hu B，Zhou T，et al.Mutual Selection Model for Weighted Networks［J］.Physical Review E，2005，72（4）：046140.

［14］ Xie Y B，Wang W X，Wang B H. Modeling the Coevolution of Topology and Traffic on Weighted Technological Networks［J］.Physical Review E，2007，75（2）：026111.

［15］ Barrat A，Barthélemy M，Vespignani A. Weighted Evolving Networks：Coupling Topology and Weight Dynamics［J］.Physical Review Letters，2004，92（22）：228701.

［16］ Newman M E J.TheStructure and Function of Complex Networks［J］.SIAM Review，2003，45（2）：167-256.

［17］ 王丹，金小峥.可调聚类系数加权无标度网络建模及其拥塞问题研究［J］.物理学报，2012，61（22）：228901.（Wang Dan，Jin Xiaozheng. On Weightd Scale-free Network Model with Tunable Clustering and Congesstion［J］.Acta Physica Sinica，2012，61（22）：228901.）

［18］ Wang W X，Hu B，Wang B H，et al.A Mutual Attraction Model for both Assortative and Disassortative Weighted Networks［J］.Physical Review E，2006，73（1）：016133.

［19］ 潘灶烽，汪小帆.一种可大范围调节聚类系数的加权无标度网络模型［J］.物理学报，2006，55（8）：4058-4064.（Pan Zaofeng，Wang Xiaofan.A Weighted Scale-free Network Model with Large-scale Tunable Clustering［J］.Acta Physica Sinica，2006，55（8）：4058-4064.）

［20］ 郝彬彬.复杂网络结构与同步控制的研究［D］.沈阳：东北大学，2009.（Hao Binbin.Structure and Synchronization of Complex Network ［D ］. Shenyang： Northeastern University，2009.）

［21］ Kumpula J M，Onnela J P，Saramäki J，et al.Emergence of Communities in Weighted Networks［J］.Physical Revlew Letters，2007，99（22）：228701.

［22］ Newman M E J.TheStructure and Function of Complex Networks［J］.SIAM Review，2003，45（2）：167-256.