具有离散时滞的两种群合作系统的稳定性

陈凤德，陈婉琳，赵 亮

（福州大学 数学与计算机科学学院，福建 福州 350108）

经典的两种群Lotka-Volterra合作系统可以表示为

由文献［1-2］可知，对该系统而言，条件

足以保证系统（1）存在唯一的全局吸引的正平衡点.

考虑到现实的生物数学模型不可避免地都要受到历史状态的影响，在系统（1）中进一步考虑时滞的影响，Chen等人［3］提出了如下模型：他们给出了两个反例表明对这类系统而言，由于时滞的作用，在条件（2）成立的情况下，系统（3）存在无界解.也就是说，系统（2）不足以保证系统（3）是持久的，从而也就更不可能保证系统（3）有全局稳定的正平衡点.他们猜测，对系统（3）而言，稳定性应该与时滞之间的比值等有关系.系统（3）中，τ1，τ3的存在，使得系统是纯时滞系统.最近的研究［4-5］表明，对纯时滞系统，时滞将会对系统的稳定性起到非常重要的作用，τ1，τ3要足够小才有可能保证系统的稳定性.因此，暂不考虑τ1，τ3，先研究如下较为简单的模型：

基于系统的生态学意义，本文恒设系统（4）满足如下初始条件：

式中，φi（s）（i＝1，2）是［-τ，0］上的连续函数，τ＝max｛τi｝（i＝2，4）.问题是：对系统（4），条件（2）是否足够保证系统存在唯一的全局吸引的正平衡点？本文旨在发展文献［4-8］的研究方法，通过构造适当的Lyapunov泛函，对该问题给出肯定的回答.

引理1 系统（4）满足初值条件（5）的解x1（t）＞0，x2（t）＞0（t≥0）.

证明

作为文献［6］定理2.2的直接推论，关于系统（4）的持久性，有如下≡结论：

引理2 若条件（2）成立，则满足初值条件（5）的系统（4）是持久≡的，即存在与系统的解无关的正常数m和M，使得系统（4）的任一正解均满足

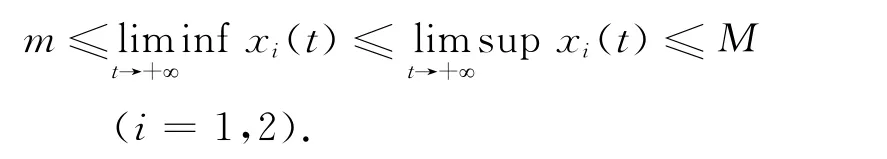
定理 假设条件（2）成立，则满足初值条件（5）的系统（4）存在唯一的全局吸引的正平衡点.

证明 计算易知，在条件（2）成立的情况下，系统（4）有唯一的正平衡点（x＊1，x＊2），其中

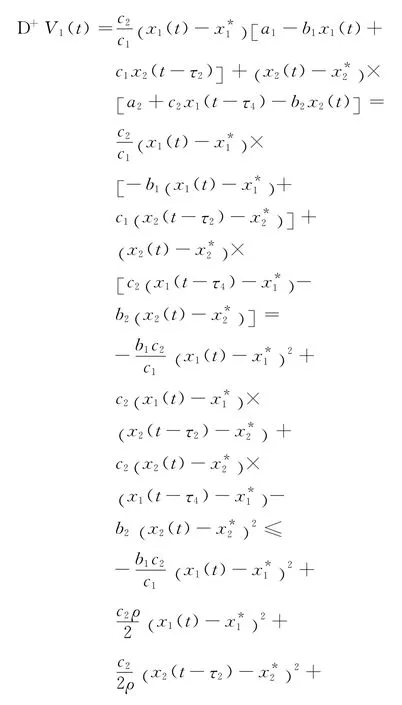
注：定理表明，系统（4）中，时滞不影响系统的稳定性，这说明时滞是无害时滞.

［1］ 马知恩.种群生态学的数学建模与研究［M］.合肥：安徽教育出版社，1996.（Ma Zhien. Mathematical Modeling and Study on Population Ecology ［M ］. Hefei：Anhui Education Press，1996.）

［2］ 陈兰荪，宋新宇，陆征一.数学生态学模型与研究方法［M］.成都：四川科学技术出版社，2003.（Chen Lansun，Song Xinyu，Lu Zhengyi. Models and Methods of Mathematical Ecology［M］.Chengdu：Sichuan Science and Technology Press，2003.）

［3］ Chen L S，Lu Z Y，Wang W D.The Effect of Delays on the Permanence for Lotka-Volterra Systems［J］. Applied Mathematics Letters，1995，8（4）：71-73.

［4］ Chen F D.Global Asymptotic Stability in n-species Nonautonomous Lotka-Volterra Competitive Systems with Infinite Delays and Feedback Control［J］. Applied Mathematics and Computation，2005，170（2）：1452-1468.

［5］ Chen F D.Global Stability of a Single Species Model with Feedback Control an Distributed Time Delay［J］.Applied Mathematics and Computation，2006，178（2）：474-479.

［6］ 林玉花，陈凤德，王海娜，等.一类非自治两种群浮游生物相克模型的持久性和全局吸引性［J］.沈阳大学学报：自然科学版，2012，24（6）：7-10.（Lin Yuhua，Chen Fengde，Wang Haina，et al.Permanence and Global Attractivity of a Nonautonomous Two Species Allelopathic Phytoplankton Model［J］.Journal of Shenyang University：Natural Science，2012，24（6）：7-10.）

［7］ 王海娜，陈凤德，林玉花，等.具有反馈控制的非自治两种群浮游生物相克系统的持久性和全局吸引性［J］.沈阳大学学报：自然科学版，2013，25（3）：173-176.（Wang Haina，Chen Fengde，Lin Yuhua，et al.Permanence and Global Attractivity of Non-Autonomous Allelopathic Phytoplankton Model for Two Species with Feedback Controls［J］.Journal of Shenyang University：Natural Science，2013，25（3）：173-176.）

［8］ Lin S Q，Lu Z Y.Permanence for Two-species Lotka-Volterra System with Delays［J］.Mathematical Biosciences and Engineering，2006，3（1）：137-144.