电力线中归一化最小和算法优化分析﹡

李虎跃， 侯 嘉， 周刘蕾， 陈 琨

(①苏州大学 电子信息学院，江苏 苏州 215006; ②93508部队综合技术站，北京 100061)

0 引言

电力线通信技术已经成为现代通信研究领域的一个重要分支，并具备广阔的产业化应用前景。ITU-T的G.hn标准化项目，更是为这一技术的实际应用提供了保障。但是电力线通信也有它的不足，因为电力线不是为了信息传输来设计搭建的，信号会受到高频脉冲噪声的影响，传输会十分不稳定。在用电的高峰期尤其明显，会造成误码率（BER）偏高，接收装置无法正确解码[1]。 因此最接近香农极限的LDPC编解码技术被G.hn标准采用来有效对抗窄带脉冲噪声。在分析几种常用的LDPC解码算法的基础上, 针对电力线信道的特点, 对归一化最小和（Normalized BP-Based）算法[2]中的修正因子进行了优化，在保持较低解码复杂度的情况下，提高了译码准确度。

1 脉冲噪声模型

Middleton A类噪声[3]一般用来模拟脉冲噪声，它将噪声分为背景噪声和脉冲噪声的和，通过对其中参数的调整可以很接近实验值，所以应用十分广泛。其中A类噪声的带宽比接收系统的小，适合用来表示电力线上的窄带脉冲噪声信号。根据A类脉冲噪声的模型，噪声的幅度 v的概率密度（PDF）表示为：

2 LDPC译码算法

低密度奇偶校验码（LDPC）[5]是目前发现的最接近香农极限的一种纠错码之一。Tanner图是一种直接表示LDPC码中变量节点和校验节点对应关系的表示方法[6]。LDPC最常用的是置信度的传播译码算法（BP算法），也称为和积（SP，Sum-Product）算法，或消息传递（MP，Massage Passing）算法。整个译码过程可以看作是在 Tanner的二分图上的BP 算法的应用[7]。LLR-BP算法的具体步骤如下：

2）校验节点的更新，对于每个校验节点 m以及n ∈N( m) ，更新公式为：

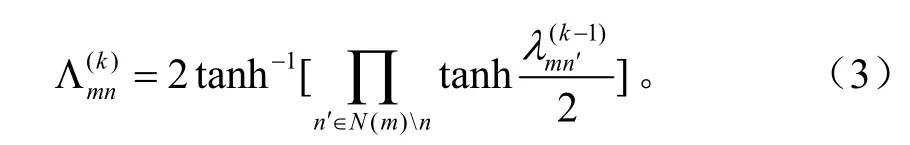
3）变量节点的更新，对于每个变量节点以及m∈M( n)，迭代遵循：

4）后验概率更新：

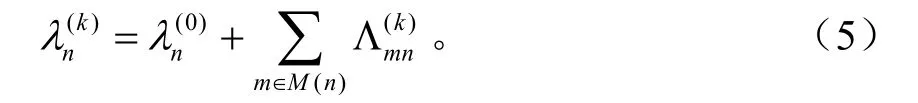
Fossorier[8]对BP算法的校验节点更新计算进行了简化处理，利用比较运算代替了查表运算，这种算法被称为BP-based，也就是最小和算法。它降低了 BP算法的计算复杂度，但译码性能有很大的下降。它与标准BP算法在校验节点的更新是不同的，最小和的校验节点的更新公式为：

最小和译码算法在误码率方面的性能的下降是比较明显的，针对这一情况 Chen提出了偏移BP-based（Offset BP-based）和归一化 BP-based（Normalized BP-based）算法。

通过分析最小和算法和标准 BP算法的不同，可以看到最小和算法相对于标准 BP算法在校验节点更新上估计值偏大。它们分别采用减法和除法来修正校验节点的信息，来获得接近于标准 BP算法的译码性能，同时在复杂度方面较最小和算法没有太大的变化。Offset BP-based和Normalized BP-based算法的校验节点的更新公式分别为：

3 针对电力线信道特征的修正因子优化

归一化BP-based算法中修正因子的选择对译码算法的误码率性能的影响很大，合理的区间选择会带来性能的提高，而不合适的修正因子的会造成LDPC译码性能的大幅下降。针对电力线信道下的算法修正因子的选择做仿真分析研究，得到了在 A类噪声电力线通信信道中的LDPC解码算法的修正因子的优化区间。

在仿真中选用的调制方式为 BPSK，设定最大的迭代次数为50，码字为G.hn标准下的QC-LDPC码，在此标准中分别给定了1/2，2/3和5/6这3种码率，码长分别为1920，1440，1152。信道噪声为Middleton A类噪声电力线信道。

在译码的过程中前几次的迭代运算对性能的影响是很大的，会对大部分的错码进行改正，所以对其进行修正会得到很好的效果，而后面的迭代过程则效率不高。经过仿真分析选定对前面的5次校验节点的更新进行修正，相对于最小和算法复杂度的增加不多，但是误码率性能得到了提高。图1、图2和图3表示不同码率下修正因子对误码率性能的影响。文中主要考虑的是信噪比在中段时的系统误码率性能，这是因为在低信噪比区域实际用途不大，而高信噪比区域的信号质量很好，最小和译码算法的误码率与 BP算法相差不多。另外修正因子的取值对于误码率的影响还是很大的,除少数几个特殊的点以外，都有一段使得误码率为最小的优化区间。不同码率的优化区间基本上是一致的，它的最优取值区间是在1.2～1.4之间。

图4、图5和图6为3种不同码率下的置信度的传播译码算法（BP），最小和算法以及归一化最小和算法的误码率性能的比较。其中归一化 BP-based算法中的修正因子这里选定了一个定值：α=1.3。从中看出相对于最小和算法，归一化 BP-based算法的误码率有了明显的下降，达到了标准的BP算法的误码率同等的水平，得到了性能的改进。

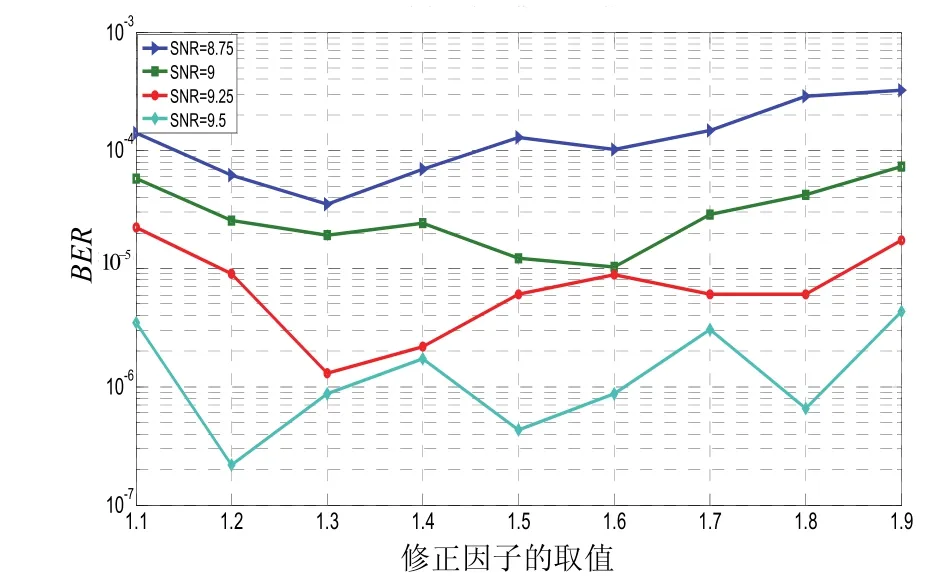
图1 码率为5/6时不同修正因子对译码性能的影响

图2 码率为2/3时不同修正因子对译码性能的影响

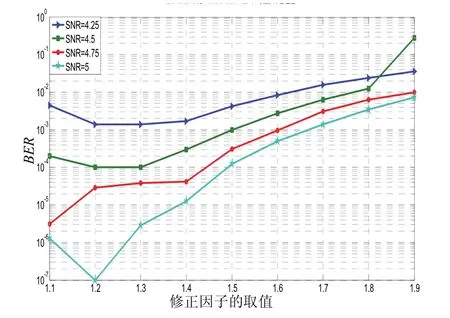
图3 码率为1/2时不同修正因子对译码性能的影响

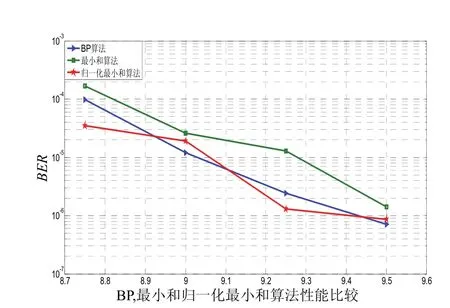
图4 码率为5/6时不同译码算法的性能比较

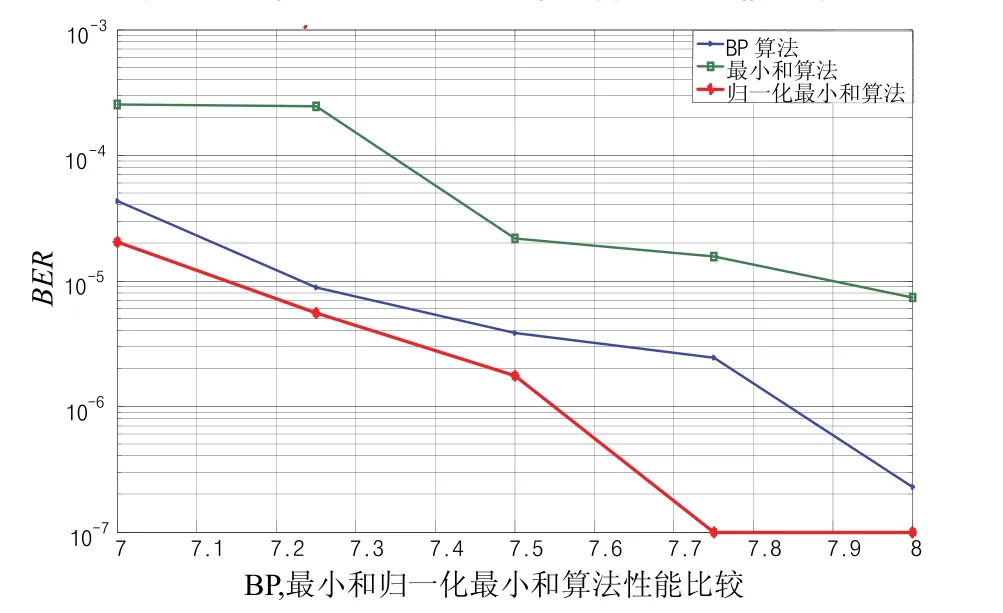
图5 码率为2/3时不同译码算法的性能比较

图6 码率为1/2时不同译码算法的性能比较

4 结语

在电力线通信中，最大的影响来自于脉冲噪声。为了抑制脉冲噪声的干扰文中采用了 LDPC信道编码技术。文中通过分析和仿真，对电力线通信中归一化最小和 LDPC译码算法的修正因子优化区间进行了选择。在复杂度增加不多的情况下，译码的准确度接近了标准BP算法，误码率有了显著地下降[9-10]。

[1]PAVLIDOU N,VINCK A J H,YAZDANI J.Power Lines Communications: State of the Art and Future Trends[J].IEEE Communication Magazine, 2003,41(04):34-40.

[2]CHEN J H, FOSSORIER M P C.Density Evolution for two Improved BP-based Decoding Algorithms of LDPC Codes[J].IEEE Communication Letters, 2002, 6(05):208-210.

[3]MIDDLETON D.Statistical-physical Model of Electromagnetic Interference[J].IEEE Trans.Electro magn.Compat,1997,19(03):106-126.

[4]尹成群,黄雷,宋文妙,等.适用于宽带电力线通信的LDPC码译码算法的研究[J].电子测量与仪器学报,2009,23(03):27-32.

[5]GALLAGER R G.Low Density Parity Check Codes[J].IRE Transactions on Information Theoroy,1962,8(01):21-28.

[6]TANNER R M.A Recursive Approach to Low Complexity Codes[J].IEEE Transactions on Information Theory,1981, 27(05):533-547.

[7]CHEN J,FOSSORIER M P C.Near Optimum Universal Belief Propagation based Decoding of Low-density Parity Check Codes[J].IEEE Tran.on Communication,2002,50(03):406-414.

[8]FOSSORIER M P C, MIHALIEVIC M, IMAI H.Reduced Complexity Iterative Decoding of Low-density Parity Check Codes based on Belief Propagation[J].IEEE Trans Commun,1999,47(05):673-680.

[9]袁李林,李贵勇.LDPC码及其应用[J].通信技术,2007,40(09):11-12.

[10]龚丽萍,陈云榕,胡凯.LDPC编译码技术研究[J].通信技术,2009,42(07):10-12.