色散管理WDM系统中简并FWM噪声的研究

杨 辉， 杜建新， 张 鑫

（南京邮电大学 光电工程学院，江苏 南京 210046）

0 引言

随着波分复用系统（WDM）的发展，脉冲间的非线性效应特别是四波混频（FWM）已成为限制WDM传输系统性能的主要因素。FWM是一种重要的非线性效应，对于等间隔的WDM系统由FWM产生的新的光场和探测信道的频率一致时，就会对探测信道产生串扰[1-3]，故分析四FWM对WDM系统性能影响程度，对优化系统性能有着重要意义。在分析时必须考虑到各种随机因素的影响[4]；基于传输光波为连续波的情况，Inoue等人考虑到比特流及脉冲初始相位的随机性，给出了强度调制／直接检测(IM／DD)及频移键控／直接检测(FSK／DD)FWM功率代价的计算，并发现在较小的功率代价情况下，FWM噪声的分布近似高斯型[5]。对于矩形脉冲波，Kumar利用频谱分析理论，考虑到信道间脉冲走离效应，给出了简并情况下的FWM噪声标准差的半解析理论计算模型[6]。当前对于传输波为啁啾高斯脉冲波的情况有了充分的研究[7]，但其所分析的系统为无集总放大的光纤链路系统。Wu等人分析了传输波为连续波的集总放大及色散补偿光纤链路中的FWM噪声，并用信噪比大小进行了量化[8]。色散管理技术是现代光网络中实现波分复用系统长距离传输的一项关键技术。基于色散管理技术的光纤链路中的各种非线性效应的研究，已经取得了一定的成果[9-10]，但缺少基于入射波为啁啾高斯脉冲时，色散管理光纤链路中FWM的研究。

理论计算模型的建立是基于已有 FWM噪声标准差模型和方法[9]，假设入射脉冲为啁啾高斯脉冲，模型中采用不同的重叠函数，具体表现为脉冲表达式的不同；同时考虑到多信道组合的情形，计算出了多个信道组合情况下的FWM噪声标准差值，详细推导了啁啾高斯脉冲在色散管理光纤链路中的振幅表达式，得出此种情况的简并FWM噪声标准差的理论计算模型。通过对此模型仿真计算，仿真计算结果分析表明：脉冲特征宽度对FWM噪声标准差的影响比较明显，FWM噪声标准差值随脉冲特征宽度的增加而增加；当归一化的特征宽度较小时，啁啾参数对FWM噪声标准差的影响不可忽略，优化的啁啾参数值可降低FWM噪声标准差；优化的色散管理方案可以使得噪声标准差有较小的值；对局部群速度色散系数绝对值进行优化，可得到较小的噪声标准差值。

1 理论计算模型

色散管理的色散图设计如图1所示,该色散图中的色散管理单元是由具有群速度色散系数符号相反、绝对值相等且长度可变的两段光纤组成，放大器间隔等于色散图周期，放大器与色散管理单元的位置关系如图1所示。修正文献[9]中的理论计算模型会发现，这一模型考虑的矩形脉冲波在光纤链路传播过程中，其波形变化幅度较小而被忽略。当入射脉冲为啁啾高斯脉冲时，啁啾高斯脉冲在光纤链路传播过程中，其脉冲形状会出现较大幅度的周期性振荡，这种脉冲形状的周期性振荡会导致理论计算模型和已有模型中的重叠函数存在差异。

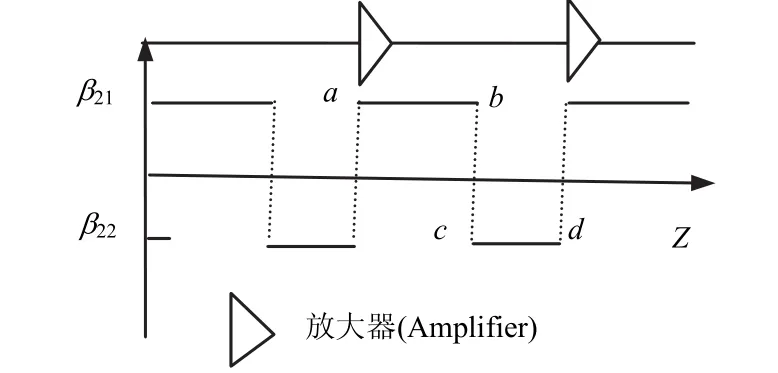
图1 色散图及放大器的设置

假设Pimax为信道i内的入射脉冲的峰值功率，T为比特周期，ni为第i信道内的比特序列中的某个比特的序号，τi～a为信道i内的比特序列在a点相对于光波在链路初始点的时延，τi～0为第i信道在链路初始点的时延；在第i信道内，设 0 ＜ τi～0＜T ,比特信息为“1”时，比特序号为ni，且峰值功率归一化的啁啾高斯脉冲在第R个色散管理单元入射点a点的光波的电场的复振幅可表示为：

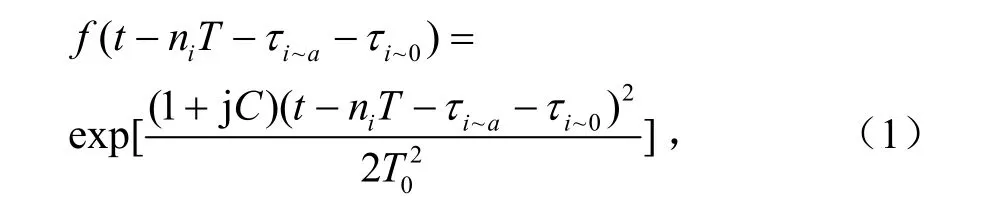
式中，C为初始啁啾参量，T0为特征宽度（光强在峰值的1/e处）。

考虑到采用色散管理的情况，在ab段内，光脉冲传输到相对a点距离为za的光场复振幅方程为：

式中，X表示前R-1段光波传输过程中的色散积累值，β21是色散图中群速度系数为正、长度为L1的群速度系数。

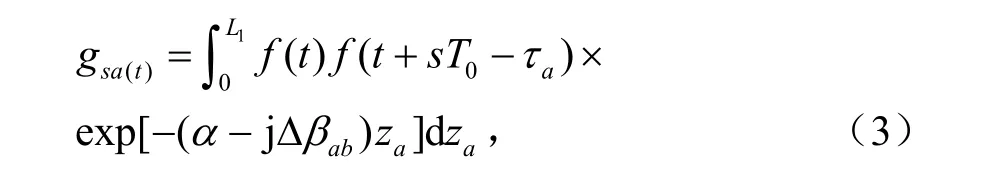
式中，Δβab为相位失配因子，aτ为第二信道相对于第一信道在脉冲传输到距离为za时的延迟：

同理可得在经过第R个色散管理单元中的cd段时，其重叠函数与段类似，考虑到位相和延迟的变化后，最大的区别在于啁啾高斯脉冲波形在色散管理单元内的不同；在第i信道内，比特序号为ni的且峰值功率归一化的啁啾高斯脉冲在色散管理单元在段内，光脉冲传输到相对c点距离为zc的光场复振幅方程为：

对文献[9]中的理论计算模型进行修正、求解FWM噪声标准差的过程中，求解出重叠函数的表达式尤为重要。对于矩形脉冲波，不考虑色散效应的情况下，重叠函数可被直接积分出解析表达式，而对于考虑到群速度色散效应的入射脉冲波为啁啾高斯脉冲的情况，重叠函数求不出解析表达式，只能得到数值积分结果。

2 仿真计算结果及讨论

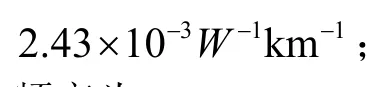
图2的参数设置：对高斯脉冲的特征宽度进行归一化处理，x轴表示脉冲的特征宽度与脉冲的初始比特周期之比（）；高斯脉冲的特征宽度随传输距离的变化而变化，这一变化对FWM噪声标准差的值产生了一定的影响。图2分3种情况进行了讨论，色散管理单元个数R分别取值为：5,8和10；各信道啁啾参数均设为0.2，局部群速度系数的绝对值为，每个色散管理单元中群速度为正的光纤长度占管理单元长度之比为0.2。由图2可以看出，噪声标准差随高斯脉冲的特征宽度增加而增加。

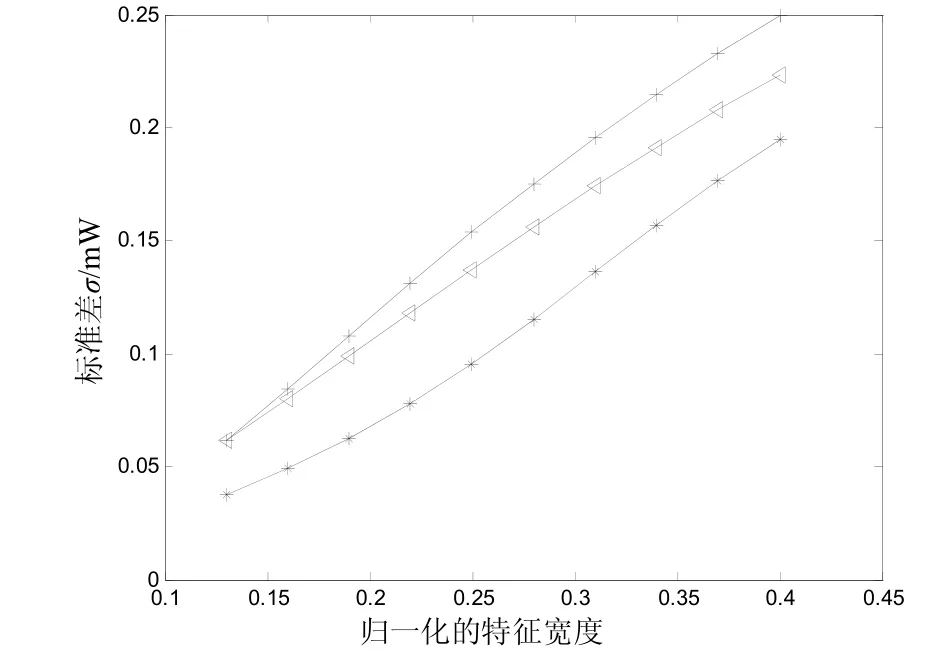
图2 σ与归一化的特征宽度T0／T的关系（▽,*,+分别对应色散周期数为5,8和10的情况）

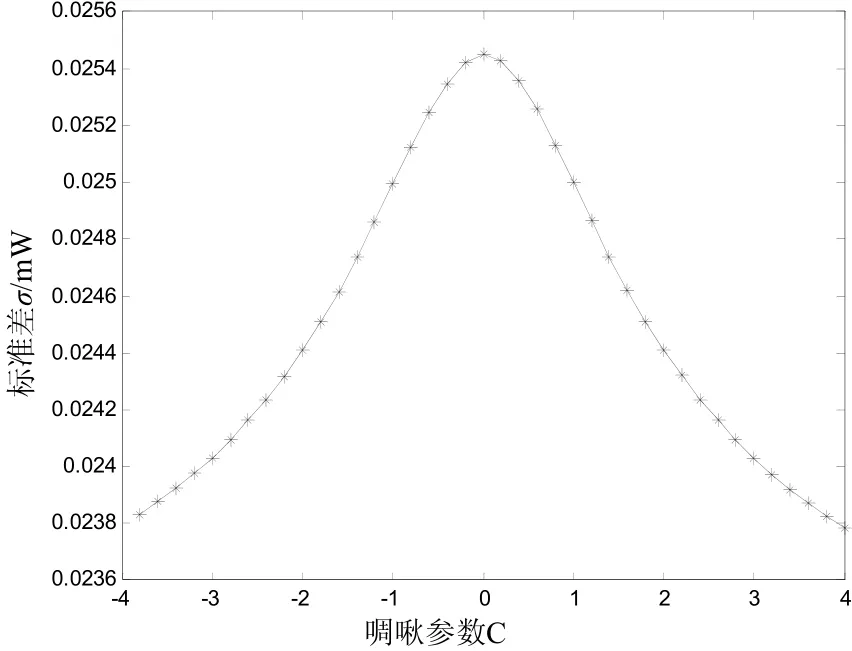
图3 σ与啁啾参数的关系（T0／T=0.05，=1ps2/km ）

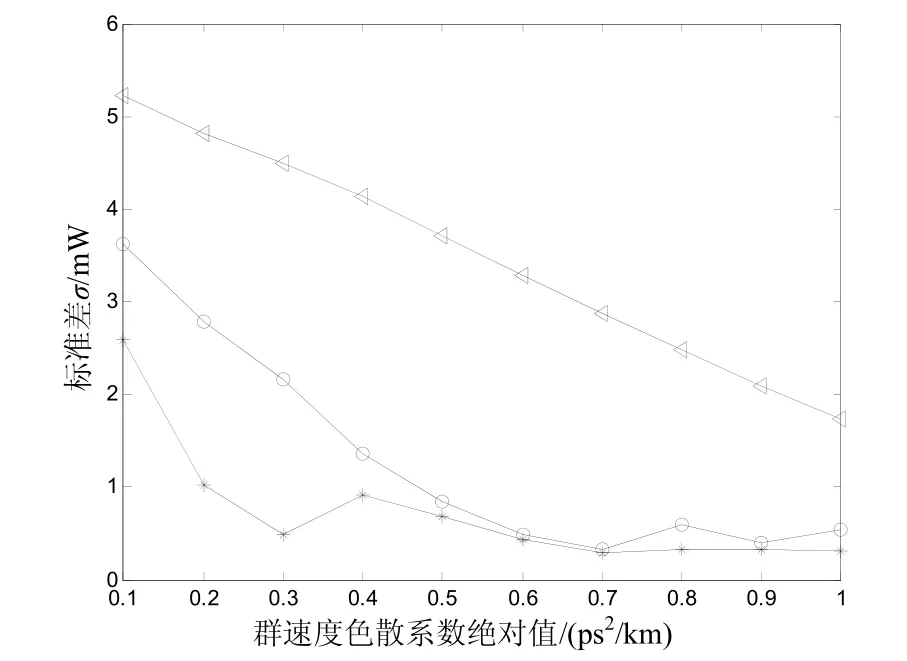
图4 σ与群速度色散系数绝对值的关系（T0／T=0.2）

3 结语

已有的强度调制直接检测波分复用系统中简并FWM噪声标准差的理论计算模型是基于入射波为连续波，或为矩形脉冲波，但没有考虑色散管理的情况以及各信道色散效应导致的脉宽展宽的情况下得到的。文中假设入射脉冲为啁啾高斯脉冲并且考虑到色散管理的情况和各信道色散效应的情况下分析了简并FWM噪声标准差与系统参数之间的一些关系，数值计算结果表明除了群速度色散、色散管理方案等是影响此种标准差的重要因素外，当入射脉冲的脉宽较小时，各信道比特序列的相对初始时延、初始啁啾参量及脉宽随距离的变化都对这种标准差的值有较大影响。

[1]INOUE K.Four-wave Mixing in an Optical Fiber in the Zero-dispersion Wavelength Region [J].J.Lightwave TechnoI.,1992,10(11):1553-1561.

[2]TKACH R W,CHRAPLYVY A R,FORGHIERI F,et a1.Fourphoton Mixing and High-speed WDM Systems[J].J.Lightwave Techno1.,1995,13(05):841-849.

[3]BOGONI A,POTI L,BONONI A.Accurate Measurement of In-band FWM Power in DWDM Systems over Nonzero Dispersion Fibers[J].IEEE Photonics Technology Letters,2003,15(02):260-262.

[4]SINKIN O V,GRIGORYAN V S,MENYUK C R.Accurate Probabilistic Treatment of Bit-pattern-dependent Nonlinear Distortions in BER Calculations for WDM RZ Systems[J].Lightwave Techno1.,2007,25(1o):2959-2967.

[5]INOUE K,NAKANISHI K,ODA K,et a1.Crosstalk and Power Penalty Due to Fiber Four-wave Mixing in Multi-channel Transmission Transmissions[J].Lightwave Techno1.,1994,l2(08):1423-1439.

[6]KUMAR S.Analysis of Degenerate Four-wave-mixing Noise in Return-to-zero Optical Transmission Systems Including Walk-of[J].Lightwave Techno1.,2005,23(01):310-320.

[7]杜建新.DWDM系统啁啾高斯脉冲简并四波混频噪声标准差的计算[J].量子电子学报,2009,26(06):736-743.

[8]WU M,WAY W I.Fiber Nonlinearity Limitations in Ultra-dense WDM Systems[J].J.Lightwave Techno1.,2004,22(06):1483-1497.

[9]杜建新.色散管理波分复用系统中的简并四波混频噪声[J].光学学报,2009,29(09):2361-2367.

[10]DU Jianxin, LOU Qihong.Collision-induced Timing Jitter in Dispersion-managed WDM Soliton System with Filtering[J].Chin.opt.Lett.,2004,2(12):688-690.

[11]朱军,柴晓冬,刘志超.多模光纤链路信号传输特性分析[J].通信技术,2008,41(10):15-16.

[12]刘飞,张晓峰,张秀珍.多路数据光纤传输系统[J].通信技术,2008,41(10):21-22.